Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Subject 5. Portfolio Risk
#cfa #cfa-level-1 #has-images #portfolio-management #risk-and-return-part-i
Consider two mutual funds, D (specialized in bonds and debt securities) and E (specialized in equity). The weight of mutual fund D in the portfolio is wD and the weight of mutual fund E is wE, and their returns are rD and rE.

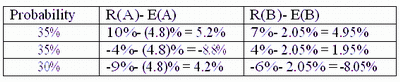
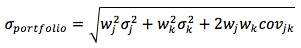
σ1 = 0.1, w1 = 0.5, σ2 = 0.1, w2 = 0.5, ρ12 = 1
Standard Deviation of Portfolio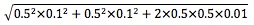 = 0.10 (perfect correlation)
= 0.10 (perfect correlation)
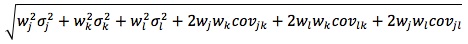
Expected return of the portfolio: E(rp) = wD E(rD) + wE E(rE)
Variance of the portfolio: σp2 = wD 2σD2 + wE2 σE2 + 2 wD wE Cov(rD, rE) = (wDσD)2 + (wEσE)2 + 2 (wDσD) (wEσE) ρDE = (wDσD + wEσE)2 + 2 (wDσD) (wEσE) (ρDE - 1) = (wDσD - wEσE)2 + 2 (wDσD) (wEσE) (ρDE + 1)
If the two assets are not perfectly positively correlated, the standard deviation of the portfolio is less than the weighted average of the standard deviations of the assets.
Covariance of returns measures the degree to which the rates of return on two securities move together over time.
- A positive covariance indicates that the rates of return on the two securities tend to move in the same direction.
- A negative covariance indicates that the rates of return on the two securities tend to move in opposite directions.
- A covariance of zero indicates that there is no relationship between the rates of return on the two securities.
The magnitude of the covariance depends on the magnitude of the individual stocks' standard deviations and the relationship between their co-movements. The covariance is an absolute measure of movement and is measured in return units squared. As the magnitude of the covariance is affected by the variability of return of each individual security, covariance cannot be used to compare across different pairs of securities.
The measure can be standardized by dividing the covariance by the standard deviations of the two securities being tested.
p(1,2) = cov(1,2)/σ1σ2
Rearranging the terms gives: cov(1,2) = p(1,2)σ1σ2.
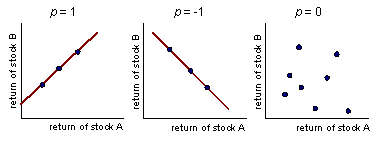
The term p(1,2) is called the correlation coefficient between the returns of securities 1 and 2. The correlation coefficient has no units. It is a pure measure of the co-movement of the two stocks' returns. It varies in the range of -1 to 1.
How should you interpret the correlation coefficient?
- A correlation coefficient of +1 means that returns always move together in the same direction. They are perfectly positively correlated.
- A correlation coefficient of -1 means that returns always move in completely opposite directions. They are perfectly negatively correlated.
- A correlation coefficient of zero means that there is no relationship between the two stocks' returns. They are uncorrelated.

Example
Two risky assets, A and B, have the following scenarios of returns:

What is the covariance between the returns of A and B?
The expected return is a probability-weighted average of the returns. Using this definition, the expected return of A is 0.35 * 10% + 0.35*(-4%) + 0.3*(9%) = 4.8%. The expected return of B is 0.35 * 7% + 0.35*(4%) + 0.3*(-6%) = 2.05%.
The covariance between the returns equals the expected value of the product of the deviations of the individual returns from their means. Remember this!
To calculate this, we construct the following table:
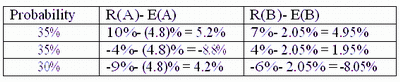
The expected value of the product of the deviations is 0.35 * 5.2% * 4.95% + 0.35 * (-8.8%) * 1.95% + 0.3*4.2%*(-8.05%) = -0.0714%.
Portfolio Risk and Return
The standard deviation of a portfolio is a function of:
- The weighted average of the individual variances, plus
- The weighted covariances between all the assets in the portfolio.
When an asset is added to a large portfolio with many assets, the new asset affects the portfolio's standard deviation in two ways. It affects:
- The asset's own variance, and
- Covariance between this asset and every other asset in the portfolio. The effect of these numerous covariances will outweigh the effect of the asset's own variance. The more assets in the portfolio, the more this is true.
Therefore, the important factor to consider when adding an investment to a portfolio is not the investment's own variance, but its average covariance with all the other investments in the portfolio.
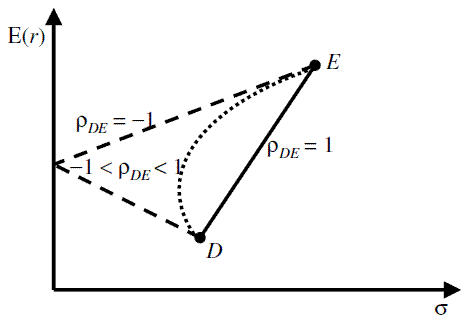
Adding securities that are not perfectly positively correlated with each other will reduce the standard deviation of the portfolio. The lower (higher) the correlations between the returns of assets in the portfolio, the lower (higher) the portfolio risk, and thus the higher (lower) the diversification benefits. The ultimate benefit of diversification occurs when the correlation between two assets is -1.00.
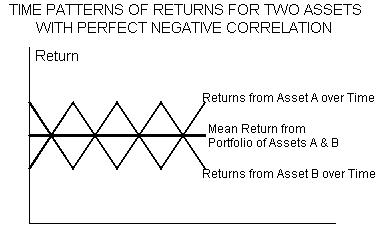
The graph below shows a portfolio with an overall standard deviation of zero, thus creating a risk-free portfolio. This occurs when two assets are combined, each moving in an opposite direction. For example, imagine a portfolio of investments, one of which moves with sun-related activities (e.g., sunglasses) and the other in the direction of rain-related activities (e.g., umbrellas). The combined portfolio of sunglasses and umbrellas ought to negate weather-related issues (theoretically speaking), as the two assets move in opposite directions.

- Returns on A move in the opposite direction from returns on B.
- The mid-point between A and B represents the mean return with no variability in returns.
- The overall standard deviation of this portfolio is zero.
- This is considered a risk-free portfolio.
In a portfolio with two assets, the ideal scenario provides a contrast in asset returns similar to the "saw tooth" diagram shown above. Thus, one asset would completely offset the other asset (in terms of risk) providing a smooth rate of return with no variability. This, of course, could only occur if the two assets had a perfect negative correlation.
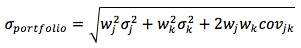
The maximum amount of risk reduction is predetermined by the correlation coefficient. Thus, the correlation coefficient is the engine that drives the whole theory of portfolio diversification.
Let's re-visit our very first example. The portfolio opportunity set shows the portfolio return and risk for different ρs.

Example with perfect positive correlation (assume equal weights)
What is the standard deviation of a portfolio (E) assuming the following data?
σ1 = 0.1, w1 = 0.5, σ2 = 0.1, w2 = 0.5, ρ12 = 1
Solution:
Cov12 = σ1 x σ2 x ρ12 = 0.1 x 0.1 x 1 = 0.01
Standard Deviation of Portfolio
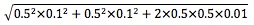 = 0.10 (perfect correlation)
= 0.10 (perfect correlation)
If there are three securities in the portfolio, its standard deviation is:
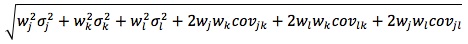
A diversification benefit is a reduction in a portfolio's standard deviation of return through diversification without an accompanying decrease in expected return. Portfolio diversification is affected by the number of assets in the portfolio and the correlation between these assets.
There are many ways to diversify investment risk.
- Diversify with asset classes.
- Diversify with index funds.
- Diversify among countries.
- Diversify by not owning your employer's stock.
- Evaluate each asset before adding it to a portfolio.
- Buy insurance for risky portfolios.
If you want to change selection, open original toplevel document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.