Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Subject 6. Efficient Frontier
#cfa #cfa-level-1 #has-images #portfolio-management #risk-and-return-part-i
The mean-variance portfolio theory says that any investor will choose the optimal portfolio from the set of portfolios that:
- Maximize expected return for a given level of risk; and
- Minimize risks for a given level of expected returns.
Again, consider a situation where you have two stocks to choose from: A and B. You can invest your entire wealth in one of these two securities. Or you can invest 10% in A and 90% in B, or 20% in A and 80%in B, or 70% in A and 30% in B, or... There are a huge number of possible combinations even in the simple case of two securities. Imagine the different combinations you have to consider when you have thousands of stocks.
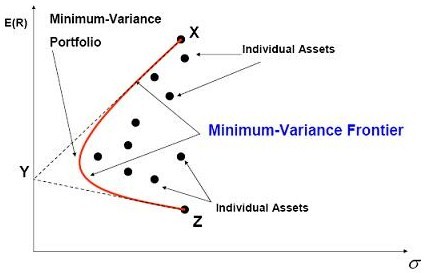
The minimum-variance frontier shows the minimum variance that can be achieved for a given level of expected return. To construct the minimum-variance frontier of a portfolio:
- Use historical data to estimate the mean, variance of each individual stock in the portfolio, and the correlation of each pair of stocks.
- Use a computer program to find the weights of all stocks that minimize the portfolio variance for each pre-specified expected return.
- Calculate the expected returns and variances for all the minimum-variance portfolios determined in step 2 and then graph the two variables.

The outcome of risk-return combinations generated by portfolios of risky assets gives you the minimum variance for a given rate of return. Logically, any set of combinations formed by two risky assets with less than perfect correlation will lie inside the triangle XYZ and will be convex.
Investors will never want to hold a portfolio below the minimum variance point. They will always get higher returns along the positively sloped part of the minimum-variance frontier.
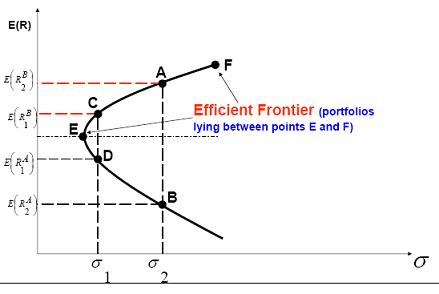
The efficient frontier is the set of mean-variance combinations from the minimum-variance frontier where, for a given risk, no other portfolio offers a higher expected return.

Any point beneath the efficient frontier is inferior to points above. Moreover, any points along the efficient frontier are, by definition, superior to all other points for that combined risk-return tradeoff.
Portfolios on the efficient frontier have different return and risk measures. As you move upward along the efficient frontier, both risk and the expected rate of return of the portfolio increase, and no one portfolio can dominate any other on the efficient frontier. An investor will target a portfolio on the efficient frontier on the basis of his attitude toward risk and his utility curves.
The concept of efficient frontier narrows down the options of the different portfolios from which the investor may choose. For example, portfolios at points A and B offer the same risk, but the one at point A offers a higher return for the same risk. No rational investor will hold the portfolio at point B and therefore we can ignore it. In this case, A dominates B. In the same way, C dominates D.
If you want to change selection, open original toplevel document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.