Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Subject 6. Bond Convexity
#basic-concepts #cfa #cfa-level-1 #fixed-income #has-images #reading-56-understanding-fixed-income-risk-and-return
Duration is a first approximation of a bond's price or a portfolio's value to rate changes. It does a good job of estimating the percentage price change for a small change in interest rates but the estimation becomes poorer the larger the change in interest rates.
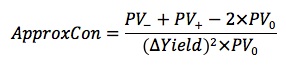
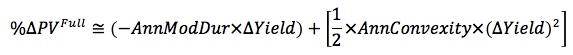
Convexity adjustment + 1.8271%
Total: - 14.8104%
The actual decrease is 14.95%, so the convexity adjustment does improve the estimate.
Duration estimate: 16.6375%
Convexity adjustment: + 1.8271%
Total: +18.4646%
Duration always gives a lower than actual price, the reason being convexity. Thus, a convexity adjustment would take into account the curvature of the price/yield relationship in order to give a more accurate estimated price.
To improve the estimate provided by duration, particularly for a large change in yield, a convexitymeasure can be used.
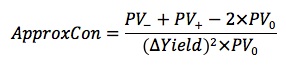
For a hypothetical 9%, 20-year bond selling to yield 6%, for a 20 basis point change in yield, P0 = 134.6722, P- = 137.5888, and P+ = 131.8439 ==> convexity measure = (131.8439 + 137.5888 - 2 x 134.6722)/(134.6722 x 0.0022) = 163.92.
Convexity indicates that as yield increases, the price of a bond declines at a declining rate. Given the convexity measure, the convexity adjustment to the duration estimate can be computed; the convexity adjustment is the amount that should be added to the duration estimate for the percentage price change.
Convexity Adjustment
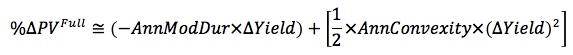
Consider a situation where you are using duration to compute the effect of a 250 basis point change in yield, where duration is 6.655 and the convexity adjustment is 1.8271. Using an estimate of modified duration, you determine that the percentage change in price of this bond resulting from a 250 basis point increase in yield should be 2.5 x -6.655 = -16.6375%. Adding the convexity adjustment, the percentage price should change by -16.6375 + 1.8271 = -14.8104%. Summarizing the price change estimates in response to the 250 basis point increase in yield, you have:
Duration estimate = -16.63750%
Convexity adjustment + 1.8271%
Total: - 14.8104%
The actual decrease is 14.95%, so the convexity adjustment does improve the estimate.
If you estimate the change resulting from a 250 basis point decrease in yield, the results can be summarized as:
Duration estimate: 16.6375%
Convexity adjustment: + 1.8271%
Total: +18.4646%
The actual percentage increase in price is 18.62%. The convexity adjustment brings the modified duration estimate closer to the actual percentage change.
If you want to change selection, open original toplevel document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.