Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Subject 8. Factors that Affect the Value of an Option
#cfa #cfa-level-1 #derivatives #has-images #los-59-k #reading-59-basics-of-derivative-pricing-and-valuation
The previous discussion tells us that the price is somewhere between zero and maximum, which is either the underlying price, the exercise price, or the present value of the exercise price - a fairly wide range of possibilities. The range will be tightened up a little on the low side by establishing a lower bound on the option price.
C0 >= Max (0, S0 - X)
P0 >= Max (0, X - S0)
If the option is in-the-money and is selling for less than its intrinsic value, it can be bought and exercised to net an immediate risk-free profit.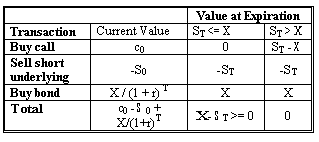
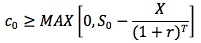
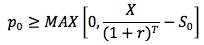
For American options, which are exercisable immediately:
C0 >= Max (0, S0 - X)
P0 >= Max (0, X - S0)
If the option is in-the-money and is selling for less than its intrinsic value, it can be bought and exercised to net an immediate risk-free profit.
However, European options cannot be exercised early; thus, there is no way for market participants to exercise an option selling for too little with respect to its intrinsic value. Investors have to determine the lower bound of a European call by constructing a portfolio consisting of a long call and risk-free bond and a short position in the underlying asset.
First the investor needs the ability to buy and sell a risk-free bond with a face value equal to the exercise price and current value equal to the present value of the exercise price. The investor buys the European call and the risk-free bond and sells short (borrows the asset and sells it) the underlying asset. At expiration the investor shall buy back the asset.
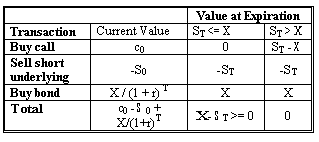
This combination produces a non-negative value at expiration, so its current value must be non-negative. For this situation to occur, the call price has to be worth at least the underlying price minus the present value of the exercise price:
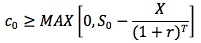
The lower bound of a European put is established by constructing a portfolio consisting of a long put, a long position in the underlying, and the issuance of a zero-coupon bond. This combination produces a non-negative value at expiration so its current value must be non-negative. For this situation to occur, the put price has to be at least as much as the present value of the exercise price minus the underlying price.
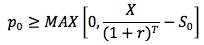
For both calls and puts, if this lower bound is negative, we invoke the rule that an option price can be no lower than zero.
Example
- All options expire in 60 days, have the same exercise price (X) of $60 and the same underlying asset.
- The current price of the underlying (S0) is $50.
- The risk-free rate (r) is 5%.
- Find the lower bounds of American and European calls and puts.
Solution
- Time to expiration (T) = 60/365 = 0.1644
- European Call (c0): MAX[0, 50 - 60/(1 + 5%)0.1644] = MAX[0, -9.52] = 0
- American Call (C0): MAX[0, 50 - 60/(1 + 5%)0.1644] = MAX[0, -9.52] = 0
- European Put (p0): MAX[0, 60/(1 + 5%)0.1644 - 50] = MAX[0, 9.52) = 9.52
- American Put (P0): MAX[0, 60 - 50) = 10
- Note that the lower bound of the American put is above the lower bound of the European put.
If you want to change selection, open original toplevel document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.