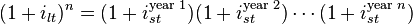Main article: expectation hypothesis
This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants' expectations of future interest rates. Using this, future rates, along with the assumption that arbitrage opportunities will be minimal in future markets, and that future rates are unbiased estimates of forthcoming spot rates, is enough information to construct a complete expected yield curve. For example, if investors have an expectation of what 1-year interest rates will be next year, the 2-year interest rate can be calculated as the compounding of this year's interest rate by next year's interest rate. More generally, rates on a long-term instrument are equal to the geometric mean of the yield on a series of short-term instruments. This theory perfectly explains the observation that yields usually move together. However, it fails to explain the persistence in the shape of the yield curve.
Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk
Yield curve - Wikipedia, the free encyclopedia
g in a credit bubble. Theory[edit] There are three main economic theories attempting to explain how yields vary with maturity. Two of the theories are extreme positions, while the third attempts to find a middle ground between the former two. <span>Market expectations (pure expectations) hypothesis[edit] Main article: expectation hypothesis This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants' expectations of future interest rates. Using this, future rates, along with the assumption that arbitrage opportunities will be minimal in future markets, and that future rates are unbiased estimates of forthcoming spot rates, is enough information to construct a complete expected yield curve. For example, if investors have an expectation of what 1-year interest rates will be next year, the 2-year interest rate can be calculated as the compounding of this year's interest rate by next year's interest rate. More generally, rates on a long-term instrument are equal to the geometric mean of the yield on a series of short-term instruments. This theory perfectly explains the observation that yields usually move together. However, it fails to explain the persistence in the shape of the yield curve. Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk Liquidity premium theory[edit] The Liquidity Premium Theory is an offshoot of the Pure Expectations Theory. The Liquidity Premium Theory asserts that long-term interest rates not only re
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |