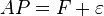Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#finance #has-images #yield-curve
available market data provides a matrix A of cash flows, each row representing a particular financial instrument and each column representing a point in time. The (i,j)-th element of the matrix represents the amount that instrument i will pay out on day j. Let the vector F represent today's prices of the instrument (so that the i-th instrument has value F(i)), then by definition of our discount factor function P we should have that F = AP (this is a matrix multiplication). Actually, noise in the financial markets means it is not possible to find a P that solves this equation exactly, and our goal becomes to find a vector P such that
where  is as small a vector as possible
is as small a vector as possible
If you want to change selection, open document below and click on "Move attachment"
Yield curve - Wikipedia, the free encyclopedia
ivate borrowing is at a premium above government borrowing, of similar maturity is a measure of risk tolerance of the lenders. For the U. S. market, a common benchmark for such a spread is given by the so-called TED spread. In either case the <span>available market data provides a matrix A of cash flows, each row representing a particular financial instrument and each column representing a point in time. The (i,j)-th element of the matrix represents the amount that instrument i will pay out on day j. Let the vector F represent today's prices of the instrument (so that the i-th instrument has value F(i)), then by definition of our discount factor function P we should have that F = AP (this is a matrix multiplication). Actually, noise in the financial markets means it is not possible to find a P that solves this equation exactly, and our goal becomes to find a vector P such that where is as small a vector as possible (where the size of a vector might be measured by taking its norm, for example). Note that even if we can solve this equation, we will only have determined P(t) for those t which have a c
Yield curve - Wikipedia, the free encyclopedia
ivate borrowing is at a premium above government borrowing, of similar maturity is a measure of risk tolerance of the lenders. For the U. S. market, a common benchmark for such a spread is given by the so-called TED spread. In either case the <span>available market data provides a matrix A of cash flows, each row representing a particular financial instrument and each column representing a point in time. The (i,j)-th element of the matrix represents the amount that instrument i will pay out on day j. Let the vector F represent today's prices of the instrument (so that the i-th instrument has value F(i)), then by definition of our discount factor function P we should have that F = AP (this is a matrix multiplication). Actually, noise in the financial markets means it is not possible to find a P that solves this equation exactly, and our goal becomes to find a vector P such that where is as small a vector as possible (where the size of a vector might be measured by taking its norm, for example). Note that even if we can solve this equation, we will only have determined P(t) for those t which have a c
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.