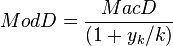Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
ModD and MacD relation
#bonds #duration #finance #has-images
well-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually):
where:
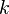is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),
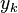is the yield to maturity for an asset, periodically compounded
If you want to change selection, open document below and click on "Move attachment"
Bond duration - Wikipedia, the free encyclopedia
uously compounded. Then expression (2) becomes: To find modified duration, when we take the derivative of the value with respect to the periodically compounded yield we find [5] Rearranging (dividing both sides by -V) gives: which is the <span>well-known relationship between modified duration and Macaulay duration: where: indexes the cash flows, is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the cash flow of the th payment from an asset, is the time in years until the th payment will be received (e.g. a two-year semi-annual would be represented by a index of 0.5, 1.0, 1.5, and 2.0), is the yield to maturity for an asset, periodically compounded is the present value of all cash payments from the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are clo
Bond duration - Wikipedia, the free encyclopedia
uously compounded. Then expression (2) becomes: To find modified duration, when we take the derivative of the value with respect to the periodically compounded yield we find [5] Rearranging (dividing both sides by -V) gives: which is the <span>well-known relationship between modified duration and Macaulay duration: where: indexes the cash flows, is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the cash flow of the th payment from an asset, is the time in years until the th payment will be received (e.g. a two-year semi-annual would be represented by a index of 0.5, 1.0, 1.5, and 2.0), is the yield to maturity for an asset, periodically compounded is the present value of all cash payments from the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are clo
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.