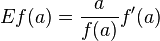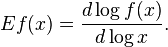In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives
meaning in words: It is thus the ratio of the relative (percentage) change in the function's output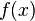 
with respect to the relative change in its input 
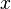, for infinitesimal changes from a point 
.
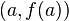In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using logarithms
meaning in words: it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument.
Elasticity of a function - Wikipedia, the free encyclopedia
er:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |