Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#bonds #duration #finance #has-images
For a small change in yield, 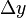 ,
,
If you want to change selection, open document below and click on "Move attachment"
Bond duration - Wikipedia, the free encyclopedia
fined above as a derivative (as the term relates to calculus) and so is based on infinitesimal changes. Modified duration is also useful as a measure of the sensitivity of a bond's market price to finite interest rate (i.e., yield) movements. <span>For a small change in yield, , Thus modified duration is approximately equal to the percentage change in price for a given finite change in yield. So a 15-year bond with a Macaulay duration of 7 years would have a Mod
Bond duration - Wikipedia, the free encyclopedia
fined above as a derivative (as the term relates to calculus) and so is based on infinitesimal changes. Modified duration is also useful as a measure of the sensitivity of a bond's market price to finite interest rate (i.e., yield) movements. <span>For a small change in yield, , Thus modified duration is approximately equal to the percentage change in price for a given finite change in yield. So a 15-year bond with a Macaulay duration of 7 years would have a Mod
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.