Ordinary annuity has a first cash flow that occurs one period from now (indexed at t = 1). In other words, the payments occur at the end of each period.
- Future value of a regular annuity
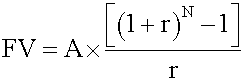
where
- A = annuity amount
- N = number of regular annuity payments
- r = interest rate per period
- Present value of a regular annuity
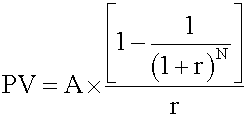
- Future value of an annuity due
This consists of two parts: the future value of one annuity payment now, and the future value of a regular annuity of (N -1) period. Calculate the two parts and add them together. Alternatively, you can use this formula:
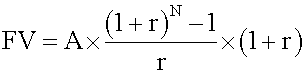
Note that, all other factors being equal, the future value of an annuity due is equal to the future value of an ordinary annuity multiplied by (1 + r).
- Present value of an annuity due
This consists of two parts: an annuity payment now and the present value of a regular annuity of (N - 1) period. Use the above formula to calculate the second part and add the two parts together. This process can also be simplified to a formula:
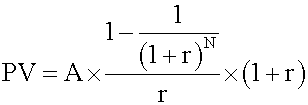
Note that, all other factors being equal, the present value of an annuity due is equal to the present value of an ordinary annuity multiplied by (1 + r).
A perpetuity is a perpetual annuity: an ordinary annuity that extends indefinitely. In other words, it is an infinite set of sequential cash flows that have the same value, with the first cash flow occurring one period from now.
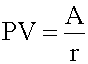
This equation is valid for a perpetuity with level payments, positive interest rate r. The first payment occurs one period from now (like a regular annuity). An example of a perpetuity is a stock paying constant dividends.
Example: Future value of a regular annuity
An analyst decides to set aside $10,000 per year in a conservative portfolio projected to earn 8% per annum. If the first payment he makes is one year from now, calculate the accumulated amount at the end of 10 years.
Method 1: Using a formula
- Identify the given variables: A = 10,000, r = 0.08, N = 10
- Identify the appropriate formula: FV = A x {[(1 + r)N - 1] / r}
- Solve for the unknown: FV = 10,000 {[(1 + 0.08)10 - 1] / 0.08} = $144,865
Texas Instruments settings:
- 2nd P/Y = 1 and key in 1 ENTER.
- SET END since this is a regular annuity. You do this by pressing 2nd BGN 2nd SET until you see END displaying. Press 2nd SET twice if necessary. After setting to END, you must always press 2nd QUIT and then continue.

Exploration: Change the problem to an annuity due (i.e., SET BGN) and compare the amounts. (The answer is $156,454.87 - a difference of $11,589.25)
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |