Money market instruments are low-risk, highly liquid debt instruments with a maturity of one year or less. There are two types of money market instruments: interest-bearing instruments (e.g., bank certificates of deposit), and pure discount instruments (e.g., U.S. Treasury bills).

Pure discount instruments such as T-bills are quoted differently than U.S. government bonds. They are quoted on a bank discount basis rather than on a price basis:

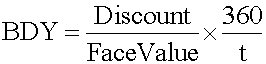
• r_BD = the annualized yield on a bank discount basis
• D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P
• t = the number of days remaining to maturity
• 360 = the bank convention of the number of days in a year.

Bank discount yield is not a meaningful measure of the return on investment because:

• It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment.
• It is annualized using a 360-day year, not a 365-day year.
• It annualizes with simple interest and ignores the effect of interest on interest (compound interest).

Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity:

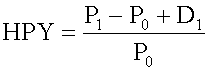
• P₀ = the initial price of the instrument
• P₁ = the price received for the instrument at its maturity
• D₁ = the cash distribution paid by the instrument at its maturity (that is, interest).

Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P₁ - P₀)/P₀.

Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield.

The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest.

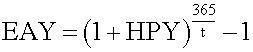
Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest.

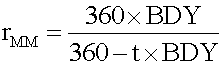
Example

An investor buys a $1,000 face-value T-bill due in 60 days at a price of $990.

• Bank discount yield: (1000 - 990)/1000 x 360/60 = 6%
• Holding period yield: (1000 - 990)/990 = 1.0101%
• Effective annual yield: (1 + 1.0101%)^365/60 - 1 = 6.3047%
• Money market yield: (360 x 6%)/(360 - 60 x 6%) = 6.0606%

If we know HPY, then:

• EAY = (1 + HPY)^365/t - 1
• r_MM = HPY x 360/t

If we know EAY, then:

• HPY = ( 1 + EAY)^t/365 - 1
• r_MM = [(1 + EAY)^t/365 - 1] x (360/t)

If we know r_MM, then:

• HPY = r_MM x (t/360)
• EAY = (1 + r_MM x t/360)^365/t - 1