Subject 6. Measures of Dispersion

Dispersion is defined as "variability around the central tendency." Investment is all about reward versus variability (risk). A central tendency is a measure of the reward of an investment and dispersion is a measure of investment risk.

There are two types of dispersions:

• Absolute dispersion is the amount of variability without comparison to any benchmark. Measures of absolute dispersion include range, mean absolute deviation, variance, and standard deviation.
• Relative dispersion is the amount of variability in comparison to a benchmark. Measures of relative dispersion include the coefficient of variance.

The range is the simplest measure of spread or dispersion. It is equal to the difference between the largest and the smallest values. The range can be a useful measure of spread because it is so easily understood. However, it is very sensitive to extreme scores because it is based on only two values. It also cannot reveal the shape of the distribution. The range should almost never be used as the only measure of spread, but it can be informative if used as a supplement to other measures of spread, such as the standard deviation or semi-interquartile range.

Example

The range of the numbers 1, 2, 4, 6,12,15,19, 26 = 26 - 1 = 25

Recall that the deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The mean absolute deviation (MAD) is the arithmetic average of the absolute deviations around the mean.

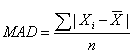
In calculating the MAD, we ignore the signs of deviations around the mean. Remember that the sum of all the deviations from the mean is equal to zero. To get around this zeroing-out problem, the mean deviation uses the absolute values of each deviation. MAD is superior to the range as a measure of dispersion because it uses all the observations in the sample. However, the absolute value is difficult to work with mathematically.

The variance is a measure of how spread out a distribution is. It is computed as the average squared deviation of each number from its mean. The formula for the variance in a population is

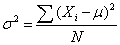
where:

• μ = the mean
• N = the number of scores

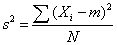When the variance is computed in a sample, the statistic(m = the mean of the sample) can be used. However, s² is a biased estimate of σ². By far the most common formula for computing variance in a sample is:

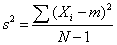
This gives an unbiased estimate of σ². Since samples are usually used to estimate parameters, s² is the most commonly used measure of variance.

The formula for the sample variance is nearly the same as that for the population variance except for the use of the sample mean, X, and the denominator. In the case of the population variance, we divide by the size of the population, N. For the sample variance, however, we divide by the sample size minus 1, or N - 1. In the math of statistics, using only N in the denominator when using a sample to represent its population will result in underestimating the population variance, especially for small sample sizes. This systematic understatement causes the sample variance to be a biased estimator of the population variance. By using (N - 1) instead of N in the denominator, we compensate for this underestimation. Thus, using N - 1, the sample variance (s²) will be an unbiased estimator of the population variance (σ²).

The major problem with using the variance is the difficulty interpreting it. Why? The variance, unlike the mean, is in terms of units squared. How does one interpret squared percentages or squared dollars? The solution to this problem is to use the standard deviation. The formula for the standard deviation is very simple: it is the square root of the variance. This is the most commonly used measure of spread. The variance indicates the adequacy of the mean as representative of the population by measuring the deviation from expectation. Basically, the variance and the standard deviation are measures of the average deviation from the mean.

An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score. In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean.

The standard deviation has proven to be an extremely useful measure of spread in part because it is mathematically tractable. Many formulas in inferential statistics use the standard deviation.

A direct comparison of two or more measures of dispersion may be difficult. For example, the difference between the dispersion for monthly returns on T-bills and the dispersion for a portfolio of small stocks is not meaningful because the means of the distributions are far apart. In order to make a meaningful comparison, we need a relative measure, to standardize the measures of absolute dispersion.

It is often useful to compare the relative variation in data sets that have different means and standard deviations, or that are measured in different units. Relative dispersion is the amount of variability present in comparison to a reference point or benchmark. The coefficient of variation (CV) is used to standardize the measure of absolute dispersion. It is defined as:

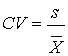
It gives a measure of risk per unit of return, and an idea of the magnitude of variation in percentage terms. It allows us direct comparison of dispersion across data sets. The lower the CV, the better; investments with low CV numbers offer less risk per unit of return. This measurement is also called relative standard deviation (RSD).

Note that because s and X-bar have the same units associated with them, the units effectively cancel each other out, leaving a unitless measure which allows for direct comparison of dispersions, regardless of the means of the data sets.

The CV is not an ideal measure of dispersion. What if the expected return is zero!? Generally, the standard deviation is the measure of choice for overall risk (and beta for individual assets).

Example

The mean monthly return on T-bills is 0.25% with a standard deviation of 0.36%. For the S&P 500, the mean is 1.09% with a standard deviation of 7.30%. Calculate the coefficient of variation for T-bills and the S&P 500 and interpret your results.

T-bills: CV = 0.36/0.25 = 1.44
S&P 500: CV = 7.30/1.09 = 6.70

Interpretation: There is less dispersion relative to the mean in the distribution of monthly T-bill returns when compared to the distribution of monthly returns for the S&P 500 (1.44 < 6.70).