Subject 7. Covariance and Correlation

Variance and standard deviation measure the dispersion of a single random variable. Often times, we want to know the relationship between two variables. For example, what is the relationship between the performance of the S&P 500 and that of U.S. long-term corporate bonds? We can use covariance and correlation to measure the degree to which two random variables are related to each other.

Given two random variables, R_i and R_j, the covariance between the two variables is:

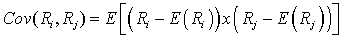
Facts about covariance:

• Covariance of returns is negative if, when the return on one asset is above its expected value, the return on the other asset is below its expected value (an average inverse relationship between returns).
• Covariance of returns is 0 if returns on the assets are unrelated.
• Covariance of returns is positive if, when the return on one asset is above its expected value, the return on the other asset is above its expected value (an average positive relationship between returns).
• The covariance of a random variable with itself (own covariance) is its own variance.

Example

Suppose that the future short-term outlook for the economy is favorable with a probability 0.6 and unfavorable with a probability of 0.4. For two stocks, F and G, returns are 0.25 and 0.2, respectively, in favorable conditions, and 0.01 and 0.02, in unfavorable conditions. Calculate cov (R_f, R_g).

We must firstly calculate the expected value of the return on each stock:
E[R_f] = 0.6 x 0.25 + 0.4 x 0.01 = 0.154
E[R_g] = 0.6 x 0.2 + 0.4 x 0.02 = 0.128

cov (R_f, R_g) = E[{R_f - E(R_f)} x {R_g - E(R_g)}] = 0.6 x [{0.25 - 0.154}x {0.2 - 0.128}] + 0.4 x [{0.01 - 0.154}x {0.02-0.128}] = 0.010368

The fact that the answer is positive indicates that the return on both stocks is above (or below) the expected value at the same time. We know that this is the case because both returns are higher in favorable conditions and lower in unfavorable conditions. Had we obtained a negative answer, logic would have told us that we had made an error somewhere.

The correlation between two random variables, R_i and R_j, is defined as:

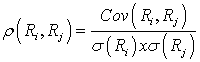
Alternative notations are corr(R_i, R_j) and ρ_ij.

Properties of correlation:

• Correlation is a number between -1 and +1.
• A correlation of 0 indicates an absence of any linear (straight-line) relationship between the variables.
• Increasingly positive correlation indicates an increasingly strong positive linear relationship (up to 1, which indicates a perfect linear relationship).
• Increasingly negative correlation indicates an increasingly strong negative linear relationship (down to -1, which indicates a perfect inverse linear relationship).

The correlation between two variables represents the degree to which these variables are related. It is important to keep in mind that correlation does not necessarily mean causation. For example, there is a high positive relationship between the number of fire-fighters sent to a fire and the amount of damage done. Does this mean that the fire fighters cause the damage? Or is it more likely that the bigger the fire, the more fire fighters are sent and the more damage is done? In this example, the variable "size of the fire" is the causal variable, correlating with both the number of fire-fighters sent and the amount of damage done.

The relationship among covariance, standard deviation, and correlation:

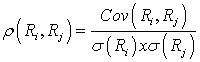
Using the figures from the previous example, we first need to calculate the two standard deviation terms:
Var(R_f) =[{R_f - E(R_f)}²] x P(R_f) = 0.6 x [{0.25-0.154}²] + 0.4 x [{0.01-0.154}²] = 0.013824. Hence, σ(R_f) = 0.117576
Var(R_g) = [{R_g - E(R_g)}²] x P(R_g) = 0.6 x [{0.2-0.128}²] + 0.4 x [{0.02-0.128}²] = 0.007776. Hence, σ(R_g) = 0.088182

Also, we know that cov(R_f,R_g) = 0.010368.

So, correlation = ρ(R_f, R_g)= cov(R_f, R_g) / σ(R_f) x σ(R_g) = 0.010368 / (0.117576 x 0.088182) = 0.99999.
This indicates an almost perfect positive linear relationship between R_f and R_g.

Calculate covariance given a joint probability function:

We can calculate covariance using the joint probability function of the random variables if that can be estimated. The joint probability function of two random variables, X and Y, denoted P(X, Y), gives the probability of joint occurrences of values X and Y. For example, P(3, 2) is the probability that X equals 3 and Y equals 2.