Subject 8. Portfolio Expected Return and Variance

The expected return on a portfolio of assets is the market-weighted average of the expected returns on the individual assets in the portfolio. The variance of a portfolio's return consists of two components: the weighted average of the variance for individual assets and the weighted covariance between pairs of individual assets.

σ²(R_p) = w₁²σ²(R₁) + w₂²σ²(R₂) + 2w₁w₂Cov(R₁, R₂)

You have a portfolio of two mutual funds, A and B, with 75% invested in A.
E(R_A) = 20%; E(R_B) = 12%.
Covariance Matrix:

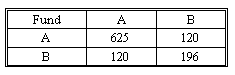
The values on the main diagonal are the variances and the other values are the covariances.

The expected return on the portfolio is:
E(R_p) = w_A E(R_A) + (1 - w_A) E(R_B) = 0.75 x 20% + 0.25 x 12% = 18%

The correlation matrix:
σ(R_A) = (625)^1/2 = 25, σ (R_B) = (196)^1/2 = 14
ρ(R_A, R_B) = Cov(R_A, R_B) / [σ(R_A) x σ(R_B)] = 120 / (25 x 14) = 0.342857, or 0.34

The variance of the portfolio is:
σ²(R_P) = w_A²σ²(R_A) + w_B²σ²(R_B) + 2w_Aw_BCov(R_A, R_B)
= (0.75)²(625) + (0.25)²(196) + 2(0.75)(0.25)(120) = 408.8125

The standard deviation is σ(R_P) = (408.8125)^1/2 = 20.22%.

It's also possible that you could be given a correlation matrix, which is simply a matrix that shows the correlation between any two assets in the portfolio. Consider the following correlation matrix for assets A, B and C.

Note that the matrix is symmetrical about its main diagonal (top left to bottom right). The entries on this diagonal are all 1, as the correlation between any variable and itself is obviously 1. Similarly, the correlation between RA and RB is 0.53, the correlation between RA and RC is 0.78, and the correlation between RB and RC is 0.6.

The steps that would now be involved would be:

• Calculate expected values and variances for the return on each asset.
• Square-root your variances in each case to get standard deviations.
• Use the standard deviations together with the correlations from the matrix above to calculate covariances using the link formula.
• Calculate the values of the portfolio weights.
• Now calculate E(Rp) and Var(Rp) using the above formula.

Essentially, the processes are the same. In each case, we need to obtain expected values, variances and covariances, in order to calculate E(Rp) and Var(Rp). How we obtain them depends on how the data are presented to us.

Familiarize yourself with the two different types of matrices, as explained in this section, and know what each term represents in each covariance formula.