Subject 10. Principles of Counting

In some cases, it's relatively easy to list and count all possible outcomes. For example, if you flip a dime in the air, there are only two possible outcomes: it will come up with either heads or tails. In other cases, there are a large number of possible outcomes. For example, imagine if you want to choose two stocks from the thousands of issues that trade on the NYSE.

If one thing can be done in n₁ ways, and a second thing, given the first, can be done in n₂ ways, and so on for k things, then the number of ways the k things can be done is n₁ x n₂ x n₃ ... x n_k.

For example, suppose a portfolio manager is making two decisions:

• Which type of instrument to invest in: stocks or bonds?
• Which country to invest in: U.S., Canada, or Germany?

The number of possible ways the manager can make these two decisions is 2 x 3 = 6.

Note that the multiplication rule is applicable if there are two or more groupings. In the preceding example, there are two groups: one for investment instruments and the other for countries. In addition, only one item can be selected from each group.

Suppose that there are n numbers in a group and n slots available. Only one member can be assigned to each slot. The number of ways to assign every number to the n slots is n factorial: n! = n x (n - 1) x (n - 2) x (n - 3) ... x 1. Note that by convention 0! = 1.

For example, five equity analysts are assigned to cover five industries. The number of ways to assign them is 5! = 5 x 4 x 3 x 2 x 1 = 120.

Unlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE.

A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):

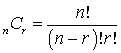
For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45.

An ordered listing is known as a permutation, and the formula that counts the number of permutations is known as the permutation formula. The number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does matter, is:

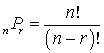
For example, if you select two of the ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. ₁₀P₂ = 10!/(10 - 2)! = 90

Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.