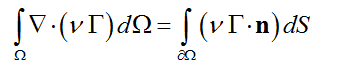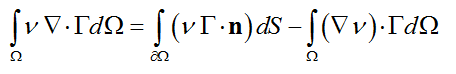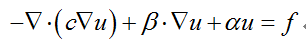Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#has-images
书写COMSOL弱形式方法  (2012-04-11 22:20:20)
(2012-04-11 22:20:20)  [imagelink]转载▼
[imagelink]转载▼
 (2012-04-11 22:20:20)
(2012-04-11 22:20:20)  [imagelink]转载▼
[imagelink]转载▼ var $tag='comsol,弱形式,偏微分方程,ped,weak,form,杂谈'; var $tag_code='4cd3575be6584db507cd9c1369e0d5ab'; var $r_quote_bligid='4a0a8b5d01012ck3'; var $worldcup='0'; var $worldcupball='0'; 标签: comsol弱形式偏微分方程pedweakform杂谈 | 分类: Comsol |
因为这方面的资料不是很多,加上属于COMSOL的高级应用,COMSOL中PDE的弱形式被神化了。实际上,跳出来看这个问题,在COMSOL中书写弱形式是非常简单的事情。
就目前我的认知水平,仅仅是应用Gauss散度定理做分部积分,再做变量替换这么简单。
下面对这个问题简单展开讨论下,个人心得,如有推导错误,请指正。
推导基础:
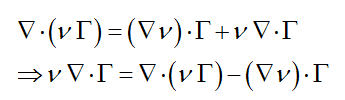 [imagelink]
[imagelink]
做积分有:
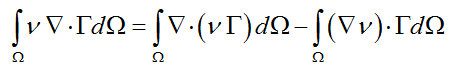 [imagelink]
[imagelink]
由Gauss公式/散度定理:
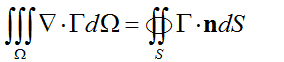 [imagelink]
[imagelink]
得到:
因此:
以对流 - 扩散 PDE 方程为例
边界条件为 Neumann 边界: 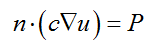 [imagelink]
[imagelink]
推导弱形式,在 PDE 方程中乘一个试函数
v 并进行积分:
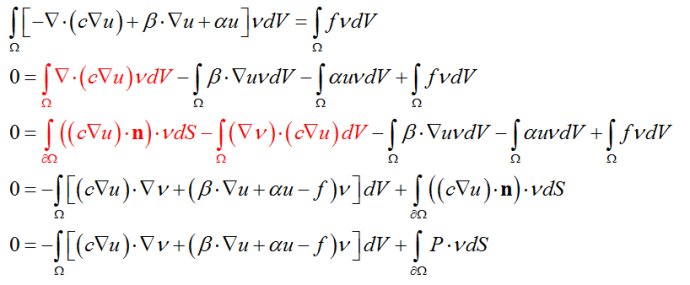 [imagelink]
[imagelink]
COMSOL中,方程的0值习惯放在方程的左边。
COMSOL的实现:将梯度写成分量形式,v写成test(u)
Weak Expressions中输入:
-c*ux*test(ux) -c*uy*test(uy)
-c*uz*test(uz)-(bx*ux+by*uy+bz*uz+a*u-f)*test(u)
边界上设定为 P*test(u)
瞬态泊松型PDE方程:
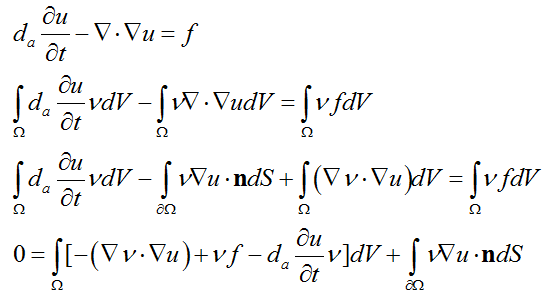 [imagelink]
[imagelink]
边界条件 u=0
COMSOL的实现:
Weak Expressions中输入:
-test(ux)*ux-test(uy)*uy+test(u)*f-da*test(u)*ut
边界上,设置约束 u
If you want to change selection, open document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.