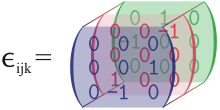
 [imagelink] Das Levi-Civita-Symbol im Dreidimensionalen repräsentiert einen besonders einfachen dreistufigen Tensor.
[imagelink] Das Levi-Civita-Symbol im Dreidimensionalen repräsentiert einen besonders einfachen dreistufigen Tensor.
Ausgehend von einem endlichdimensionalen Vektorraum bezeichnet man Skalare als Tensoren vom Typ \((0,0)\), Vektoren als Tensoren vom Typ \((1,0)\) und Kovektoren als Tensoren vom Typ \((0,1)\). Tensoren höherer Stufe definiert man als multilineare Abbildungen mit Tensoren geringerer Stufe als Argumente und Abbildungswerte. So kann etwa ein Tensor vom Typ \((1,1)\) als lineare Abbildung zwischen Vektorräumen oder als bilineare Abbildung mit einem Vektor und einem Kovektor als Argumente aufgefasst werden.
Beispielsweise ist der mechanische Spannungstensor in der Physik ein Tensor zweiter Stufe – eine Zahl (Stärke der Spannung) oder ein Vektor (eine Hauptspannungsrichtung) reichen nicht immer zur Beschreibung des Spannungszustandes eines Körpers aus. Als Tensor vom Typ \((0,2)\) aufgefasst ist er eine lineare Abbildung, die einem Flächenelement (als Vektor) die darauf wirkende Kraft (als Kovektor) zuordnet, oder eine bilineare Abbildung, die einem Flächenelement und einem Verschiebungsvektor die Arbeit zuordnet, die bei der Verschiebung des Flächenstücks unter dem Einfluss der wirkenden Spannung verrichtet wird.
Bezüglich einer fest gewählten Vektorraumbasis erhält man die folgenden Darstellungen der verschiedenen Typen von Tensoren:
- Ein Skalar durch eine einzelne Zahl.
- Ein Vektor durch einen Spaltenvektor.
- Ein Kovektor durch einen Zeilenvektor.
- Ein Tensor zweiter Stufe durch eine Matrix.
Die Anwendung des Spannungstensors auf ein Flächenelement ist dann z. B. durch das Produkt einer Matrix mit einem Spaltenvektor gegeben. Die Koordinaten von Tensoren höherer Stufe können entsprechend in ein höherdimensionales Schema angeordnet werden. So können diese Komponenten eines Tensors anders als die eines Spaltenvektors oder einer Matrix mehr als ein oder zwei Indizes haben. Ein Beispiel für einen Tensor dritter Stufe, der drei Vektoren des \(\mathbb R^3\) als Argumente hat, ist die Determinante einer 3×3-Matrix als Funktion der Spalten dieser Matrix. Bezüglich einer Orthonormalbasis wird er durch das Levi-Civita-Symbol \(\varepsilon_{ijk}\) repräsentiert.
Ko- und Kontravarianz von VektorenSummary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |