Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#has-images
In a recent program gallery post we introduced the Blum-Blum-Shub pseudorandom generator. A pseudorandom generator is simply an algorithm that takes as input a short random string of length 
and produces as output a longer string, say, of length 
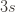. This output string should not be random, but rather “indistinguishable” from random in a sense we’ll make clear next time. The underlying function for this generator is the “modular squaring” function 
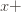, for some cleverly chosen 
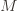. The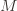 
is chosen in such a way that makes this mapping a permutation. So this function is more than just a pseudorandom generator, it’s a one-way permutation.
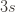and produces as output a longer string, say, of length . This output string should not be random, but rather “indistinguishable” from random in a sense we’ll make clear next time. The underlying function for this generator is the “modular squaring” function 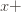, for some cleverly chosen 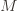. The 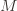is chosen in such a way that makes this mapping a permutation. So this function is more than just a pseudorandom generator, it’s a one-way permutation.If you want to change selection, open document below and click on "Move attachment"
Zero Knowledge Proofs for NP – Math ∩ Programming
s blog’s Github page. In the follow up to this post, we’ll dive into more nitty gritty details about the proof that this works, and study different kinds of zero-knowledge. One-way permutations <span>In a recent program gallery post we introduced the Blum-Blum-Shub pseudorandom generator. A pseudorandom generator is simply an algorithm that takes as input a short random string of length and produces as output a longer string, say, of length . This output string should not be random, but rather “indistinguishable” from random in a sense we’ll make clear next time. The underlying function for this generator is the “modular squaring” function , for some cleverly chosen . The is chosen in such a way that makes this mapping a permutation. So this function is more than just a pseudorandom generator, it’s a one-way permutation. If you have a primality-checking algorithm on hand (we do), then preparing the Blum-Blum-Shub algorithm is only about 15 lines of code. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2
Zero Knowledge Proofs for NP – Math ∩ Programming
s blog’s Github page. In the follow up to this post, we’ll dive into more nitty gritty details about the proof that this works, and study different kinds of zero-knowledge. One-way permutations <span>In a recent program gallery post we introduced the Blum-Blum-Shub pseudorandom generator. A pseudorandom generator is simply an algorithm that takes as input a short random string of length and produces as output a longer string, say, of length . This output string should not be random, but rather “indistinguishable” from random in a sense we’ll make clear next time. The underlying function for this generator is the “modular squaring” function , for some cleverly chosen . The is chosen in such a way that makes this mapping a permutation. So this function is more than just a pseudorandom generator, it’s a one-way permutation. If you have a primality-checking algorithm on hand (we do), then preparing the Blum-Blum-Shub algorithm is only about 15 lines of code. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.