Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Tags
#chapter-1 #has-images #jaynes_probability_theory
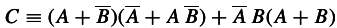
Question
This is just an example of a function. C = f(A, B)
How large is the class of new propositions thus generated?
How large is the class of new propositions thus generated?
Answer
two propositions, although they may appear entirely different when written out in the manner, are not different propositions from the standpoint of logic if they have the same truth value.
For A and B there 4 different inputs. TT, TF, etc. Size of the function: 2 -> 4, therefore there are 4^2 functions. A fixed number.
This easily generalizes to greater dimensions.
For A and B there 4 different inputs. TT, TF, etc. Size of the function: 2 -> 4, therefore there are 4^2 functions. A fixed number.
This easily generalizes to greater dimensions.
Tags
#chapter-1 #has-images #jaynes_probability_theory
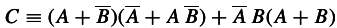
Question
This is just an example of a function. C = f(A, B)
How large is the class of new propositions thus generated?
How large is the class of new propositions thus generated?
Answer
?
Tags
#chapter-1 #has-images #jaynes_probability_theory
Question
This is just an example of a function. C = f(A, B)
How large is the class of new propositions thus generated?
How large is the class of new propositions thus generated?
Answer
two propositions, although they may appear entirely different when written out in the manner, are not different propositions from the standpoint of logic if they have the same truth value.
For A and B there 4 different inputs. TT, TF, etc. Size of the function: 2 -> 4, therefore there are 4^2 functions. A fixed number.
This easily generalizes to greater dimensions.
For A and B there 4 different inputs. TT, TF, etc. Size of the function: 2 -> 4, therefore there are 4^2 functions. A fixed number.
This easily generalizes to greater dimensions.
If you want to change selection, open document below and click on "Move attachment"
Summary
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Details
No repetitionsDiscussion
Do you want to join discussion? Click here to log in or create user.