Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Tags
#Auswertung #Interpretation #has-images
Question
Auswertung: Konfidenzintervalle
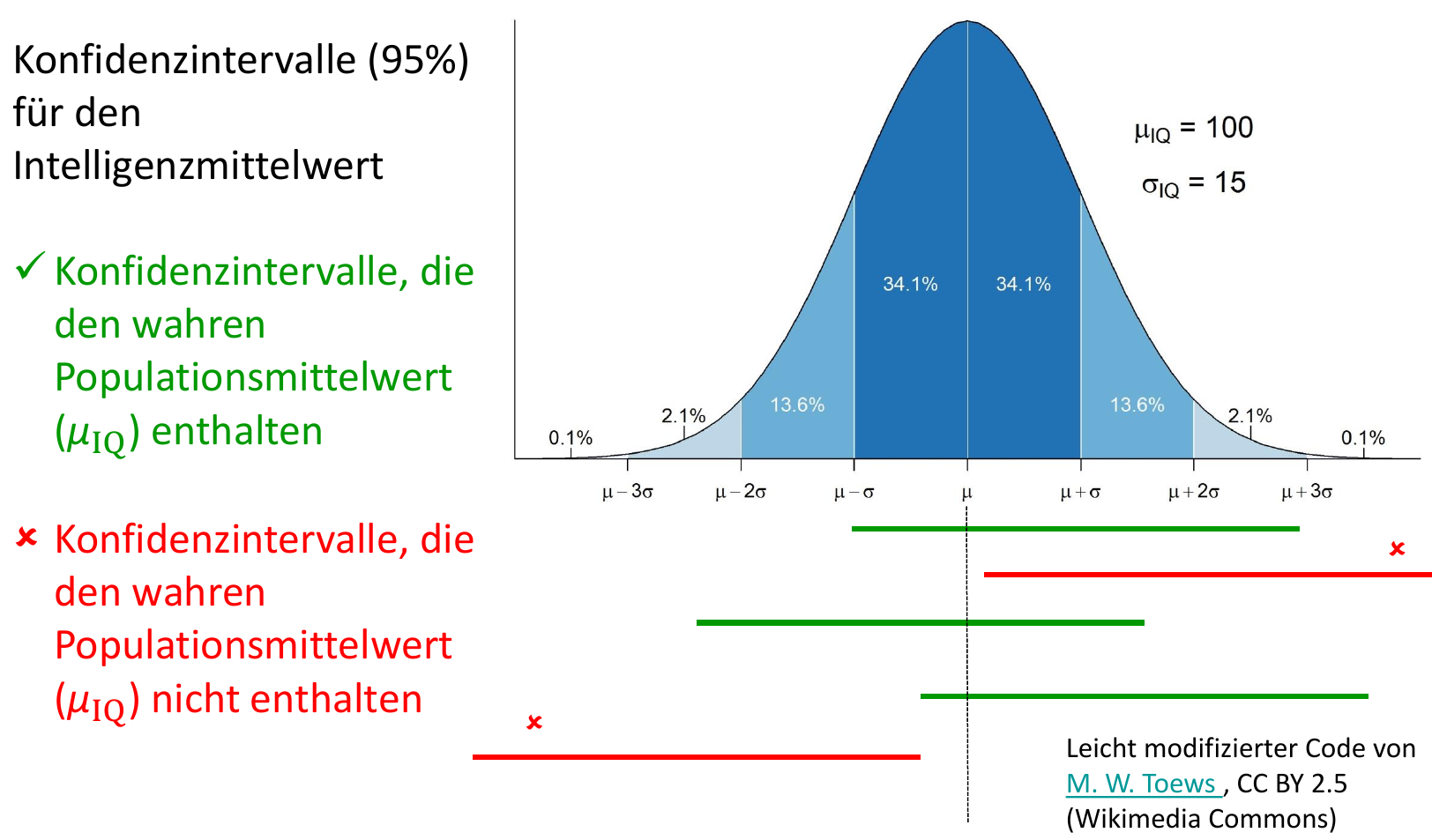
Answer
- Bestimmung statist . Signifikanz für unterschiedliche Parameter möglich
- Z.B. Mittelwert , Mittelwertdifferenz, Varianz, Effektstärken
- Z.B. Mittelwert (95% CI) = M 1.96 * SE; M = 5 [0.03; 9.97] Statist. signifikant, weil 0 nicht imcKonfidenzintervall liegt
- Z.B. Mittelwert , Mittelwertdifferenz, Varianz, Effektstärken
- Vermeintliches Unsicherheitsmaß
- Breite Intervalle als Zeichen dafür, dass der wahre Wert deutlich kleiner/größer als der berechnete Wert sein kann
- Nicht unbedingt… (vgl. Morey et al., 2016)
- Breite Intervalle als Zeichen dafür, dass der wahre Wert deutlich kleiner/größer als der berechnete Wert sein kann
- Konfidenzintervalle werden selbst von Experten (Lehrbücher etc.) falsch interpretiert
- Korrekte Interpretation: Bsp. 95% CI = Hätte man die Untersuchung unendlich häufig wiederholt, dann würde der wahre Wert in 95% der Fälle in den Konfidenzintervallen liegen
- Die Pluralform ist entscheidend: In jeder Untersuchung könnte man nämlich ein völlig anderes Konfidenzintervall bekommen
- Es gibt nur zwei Möglichkeiten: entweder befindet sich der wahre Wert im Konfidenzintervall ( p = 1) oder nicht p = 0). Die Wahrscheinlichkeit kann also nicht 95%, 99% etc. betragen
- Leider wissen wir nicht, ob der wahre Wert in einem konkreten Intervall liegt. Wenn man Pech hat, dann liegen sogar völlig unplausible Werte im Konfidenzintervall
- Die Nützlichkeit der Konfidenzintervalle sehr umstritten
- Alternative: Bayessche Statistik, z.B. 95% Credibility interval --> In welchem Bereich liegen die plausibelsten Werte?
- Leider wissen wir nicht, ob der wahre Wert in einem konkreten Intervall liegt. Wenn man Pech hat, dann liegen sogar völlig unplausible Werte im Konfidenzintervall
Tags
#Auswertung #Interpretation #has-images
Question
Auswertung: Konfidenzintervalle
Answer
?
Tags
#Auswertung #Interpretation #has-images
Question
Auswertung: Konfidenzintervalle

Answer
- Bestimmung statist . Signifikanz für unterschiedliche Parameter möglich
- Z.B. Mittelwert , Mittelwertdifferenz, Varianz, Effektstärken
- Z.B. Mittelwert (95% CI) = M 1.96 * SE; M = 5 [0.03; 9.97] Statist. signifikant, weil 0 nicht imcKonfidenzintervall liegt
- Z.B. Mittelwert , Mittelwertdifferenz, Varianz, Effektstärken
- Vermeintliches Unsicherheitsmaß
- Breite Intervalle als Zeichen dafür, dass der wahre Wert deutlich kleiner/größer als der berechnete Wert sein kann
- Nicht unbedingt… (vgl. Morey et al., 2016)
- Breite Intervalle als Zeichen dafür, dass der wahre Wert deutlich kleiner/größer als der berechnete Wert sein kann
- Konfidenzintervalle werden selbst von Experten (Lehrbücher etc.) falsch interpretiert
- Korrekte Interpretation: Bsp. 95% CI = Hätte man die Untersuchung unendlich häufig wiederholt, dann würde der wahre Wert in 95% der Fälle in den Konfidenzintervallen liegen
- Die Pluralform ist entscheidend: In jeder Untersuchung könnte man nämlich ein völlig anderes Konfidenzintervall bekommen
- Es gibt nur zwei Möglichkeiten: entweder befindet sich der wahre Wert im Konfidenzintervall ( p = 1) oder nicht p = 0). Die Wahrscheinlichkeit kann also nicht 95%, 99% etc. betragen
- Leider wissen wir nicht, ob der wahre Wert in einem konkreten Intervall liegt. Wenn man Pech hat, dann liegen sogar völlig unplausible Werte im Konfidenzintervall
- Die Nützlichkeit der Konfidenzintervalle sehr umstritten
- Alternative: Bayessche Statistik, z.B. 95% Credibility interval --> In welchem Bereich liegen die plausibelsten Werte?
- Leider wissen wir nicht, ob der wahre Wert in einem konkreten Intervall liegt. Wenn man Pech hat, dann liegen sogar völlig unplausible Werte im Konfidenzintervall
If you want to change selection, open document below and click on "Move attachment"
pdf
cannot see any pdfs
Summary
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Details
No repetitionsDiscussion
Do you want to join discussion? Click here to log in or create user.