Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#causality #has-images #statistics
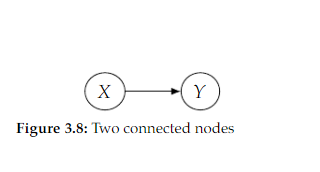

For example, if the DAG were simply two connected nodes 𝑋 and 𝑌 as in Figure 3.8, the local Markov assumption would tell us that we can factorize 𝑃(𝑥, 𝑦) as 𝑃(𝑥)𝑃(𝑦|𝑥) , but it would also allow us to factorize 𝑃(𝑥, 𝑦) as 𝑃(𝑥)𝑃(𝑦) , meaning it allows distributions where 𝑋 and 𝑌 are independent. In contrast, the minimality assumption does not allow this additional independence. Minimality would tell us to factorize 𝑃(𝑥, 𝑦) as 𝑃(𝑥)𝑃(𝑦|𝑥) , and it would tell us that no additional independencies (𝑋 ⊥⊥ 𝑌) exist in 𝑃 that are minimal with respect to Figure 3.8.
If you want to change selection, open document below and click on "Move attachment"
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.