BuboFlash - helps with learning

Edited, memorised or added to reading queue

Do you want BuboFlash to help you learning these things? Click here to log in or create user.

Annotation 149623697

#bonds #finance #yield-to-maturity

for zero coupon bonds, the yield to maturity and the rate of return are equivalent since there are no coupon payments to reinvest.
it is dubious. YTM is not about reinvesting coupons

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Yield to Maturity
ng period return, as the two often differ. Yield to maturity is generally given in terms of Annual Percentage Rate (APR), and it is an estimation of future return, as the rate at which coupon payments can be reinvested at is unknown. However, for zero coupon bonds, the yield to maturity and the rate of return are equivalent since there are no coupon payments to reinvest. Another way of putting it is that the yield to maturity is the rate of return that makes the present value (PV) of the cash flow generated by the bond equal to the price. Yield to maturi

Annotation 149623941

#finance #yield-curve

at the short end of the curve, where there are few cashflows, the first few elements of P (rate function) may be found by bootstrapping from one to the next.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Yield curve - Wikipedia, the free encyclopedia
orward interest rates, zero coupon bond prices, or zero coupon bond yieldsLocal regression using kernelsLinear programming In the money market practitioners might use different techniques to solve for different areas of the curve. For example at the short end of the curve, where there are few cashflows, the first few elements of P may be found by bootstrapping from one to the next. At the long end, a regression technique with a cost function that values smoothness might be used. How the yield curve affects bond prices[edit] There is a time dimension to the analysis

Annotation 149623974

indexing elements in matrix

#has-images #linear-algebra #mathematics #matrices

Each element of a matrix is often denoted by a variable with two subscripts. For instance, a_2,1 represents the element at the second row and first column of a matrix A.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Matrix (mathematics) - Wikipedia, the free encyclopedia
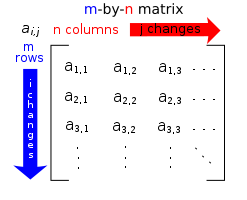
Matrix (mathematics) From Wikipedia, the free encyclopedia Jump to: navigation, search "Matrix theory" redirects here. For the physics topic, see Matrix string theory. Each element of a matrix is often denoted by a variable with two subscripts. For instance, a2,1 represents the element at the second row and first column of a matrix A. In mathematics, a matrix (plural matrices) is a rectangular array[1] of numbers, symbols, or expressions, arranged in rows and columns.[2][3] The individual items in a matrix are called

Annotation 149624179

yield to maturity - reinvesting coupons

#bonds #finance #yield-to-maturity

All the coupons are reinvested at an interest rate equal to the yield-to-maturity - it is a common mistaken assumption, but not true. Each part of today's price earns interest before being paid out either as a coupon or as a principal.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Yield to maturity - Wikipedia, the free encyclopedia
ds6 See also7 References8 External links Main assumptions[edit] The main underlying assumptions used concerning the traditional yield measures are: The bond will be held to maturity.All coupon and principal payments will be made on schedule.All the coupons are reinvested at an interest rate equal to the yield-to-maturity.[3]The yield is usually quoted without making any allowance for tax paid by the investor on the return, and is then known as "gross redemption yield". It also does not make an

Flashcard 149624929

Tags

#bonds #duration #finance

Question

Does Macaulay duration use future values of cashflows or present values of cashflows for weighting by time?

Answer

present value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 149624949

#bonds #duration #finance

Portfolio has to have duration (rather than maturity) equal to the required period, but it needs constant adjusting, because duration is calculated from yield to maturity so when yield changes, so does duration. Also, it is not accurate because immunisation is only to parallel shifts in rates.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 149624993

Tags

#bonds #finance

Question

When a bond sells at a discount, what is the relation between YTM, current yield and coupon yield?

Answer

YTM > current yield > coupon yield

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
The concept of current yield is closely related to other bond concepts, including yield to maturity, and coupon yield. The relationship between yield to maturity and the coupon rate is as follows: When a bond sells at a discount, YTM > current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield

Original toplevel document

Bond valuation - Wikipedia, the free encyclopedia
s simply the coupon payment as a percentage of the face value . Coupon yield is also called nominal yield. Current yield[edit] The current yield is simply the coupon payment as a percentage of the (current) bond price . Relationship[edit] The concept of current yield is closely related to other bond concepts, including yield to maturity, and coupon yield. The relationship between yield to maturity and the coupon rate is as follows: When a bond sells at a discount, YTM > current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield Price sensitivity[edit] Main articles: Bond duration and Bond convexity The sensitivity of a bond's market price to interest rate (i.e. yield) movements is measured by its duration, and,

Flashcard 149625004

Tags

#bonds #finance

Question

When a bond sells at a premium, what's the relation between YTM, coupon yield and current yield?

Answer

coupon yield > current yield > YTM

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
is closely related to other bond concepts, including yield to maturity, and coupon yield. The relationship between yield to maturity and the coupon rate is as follows: When a bond sells at a discount, YTM > current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield<body><html>

Original toplevel document

Flashcard 149625022

Tags

#bonds #finance

Question

When a bond sells at par, what's the relation between YTM, current yield and coupon yield?

Answer

YTM = current yield = coupon yield

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
and coupon yield. The relationship between yield to maturity and the coupon rate is as follows: When a bond sells at a discount, YTM > current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield<body><html>

Original toplevel document

Annotation 149625039

#calculus #economics #mathematics

Constant slope does not imply constant elasticity. To see this, consider the linear demand function Q=a-bP, which has constanst slope equal -b. But the elasticity implied by this demand function is E=(dQ/dP)(P/Q)=-b(P/Q). Since the ratio P/Q gets smaller and smaller as Q increases, demand is more leastic at high prices and less elastic at low prices.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Elasticity vs. Slope?
Best Answer helper answered 5 years ago Constant slope does not imply constant elasticity. To see this, consider the linear demand function Q=a-bP, which has constanst slope equal -b. But the elasticity implied by this demand function is E=(dQ/dP)(P/Q)=-b(P/Q). Since the ratio P/Q gets smaller and smaller as Q increases, demand is more leastic at high prices and less elastic at low prices. This makes intuitive sense, since it is reasonable that quantity demanded is more sensitive at high prices than it is at low prices. A demand function of the form Q=b/P is called a constant elasticity demand function. To see this, note that E=(dQ/dP)(P/Q)=(-b/P^2)(P/Q)=(-b/P^2)(P/... a constant. More generally, if

Flashcard 149625084

Question

responsible

Answer

edit answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Wikipedia, the free encyclopedia
lopedia that anyone can edit. 4,549,964 articles in English ArtsBiographyGeography HistoryMathematicsScience SocietyTechnologyAll portals From today's featured article No. 34 Squadron is a Royal Australian Air Force (RAAF) squadron, responsible for the transport of VIPs, including members of the Australian government, the Governor-General, and visiting dignitaries. The squadron has a secondary role providing emergency transport

Edited, memorised or added to reading queue

on 07-Jul-2014 (Mon)

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document