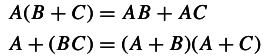Answer
"A implies B" really does not mean that there is a chain of arguments so you can derive B from what's inside the statement A. "A implies B" indeed only means "whenever A, then B". You can say "the fact that the number 3 is odd implies that the number 100 is bigger than the number 50". "Implies" here really doesn't mean that you can derive size relations of numbers from the oddness of other numbers by looking at the concepts of "size" and "oddness". These statements haven't anything special to do with each other, they just happen to be both true.
And every true statement "follows from" / "is implied by" every other true statement in the sense of formal logic.
every statement (be it true or false) "is implied by" / "follows from" any false statement.