Edited, memorised or added to reading queue
on 10-Jun-2020 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 5510566645004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThrough our educational platform Kwik Learning, we have students in 195 countries and have generated tens of millions of podcast downloads. Our community has expressed a growing concern about their overreliance on technology and they come to us to upgrade their brains to find relief from these “four horsemen” of our age: digital deluge, digital distraction, digital dementia, and digital deduction. It’s important to note that overload, distraction, forgetfulness, and default thinking have been around for ages. While technology doesn’t cause these conditions, it has great potential to amplify them. The benefits of the digital age are plentiful, but let’s take a look at how the advances in technology that help you, can possibly also hinder you.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5510570839308
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
田村虎蔵 - Wikipedia
田村虎蔵 - Wikipedia 田村虎蔵 出典: フリー百科事典『ウィキペディア(Wikipedia)』 ナビゲーションに移動 検索に移動 [imagelink] [emptylink] 田村虎蔵(1910年頃) 田村 虎蔵(たむら とらぞう、1873年 5月24日 - 1943年 11月7日 )は、日本の音楽教育家、作曲家。鳥取県 岩美郡 馬場村(現・岩美町 馬場)生まれ、蒲生小学校 卒業、 鳥取高等小学校 、鳥取県尋常師範学校 。東京音楽学校 卒。 東京音楽学校、東京高等師範学校 助教授。言文一致唱歌 を提唱し、納所弁次郎 らと「幼年唱歌 」(1900年)「尋常小学唱歌 」などを編集。1922年西洋に渡り音楽教育事情を研究、帰国後は、東京市 音楽担当視学 となる。弟子に堀内敬三 がいる。
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
田村虎蔵 - Wikipedia
田村虎蔵先生記念刊行会編 目黒書店 1933年 『名作唱歌選集』故田村虎蔵先生記念会編 音楽之友社 1950年 伝記[編集 ] 丸山忠璋 『言文一致唱歌の創始者田村虎蔵の生涯』音楽之友社 1998年 史蹟[編集 ] 田村虎蔵先生之生地 鳥取県 岩美郡 岩美町 馬場 碑と像が建てられている。 田村虎蔵旧居跡 東京都 新宿区 筑土八幡町 4-24 区指定史蹟。由緒の書かれた案内板がある。 <span>田村虎蔵先生をたたえる碑 東京都新宿区筑土八幡町2-1 筑土八幡神社 入口。金太郎の一節と由緒の書かれた碑が建てられている。 関連項目[編集 ] 鉄道唱歌 電車唱歌 帝国音楽学校 島崎赤太郎 わらべ館 八波則吉 朝鮮藝術賞 みんなの童謡 唱歌 (教科) 花咲か爺 日本音楽文化協会 平忠度 広瀬武夫 外部リンク[編集 ] コトバンク わらべ館 典拠管理 WorldCat Identities ISNI : 0000 0000 8235 7732 LCCN : nr2003005715 Musi
Flashcard 5525554728204
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525555776780
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525568097548
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe reader is encouraged to pay special attention to the distinctions between the different concepts introduced here. These concepts include the notions of a body, a configuration of the body, a reference configuration of the body, the region occupied by the body in some configuration, a particle (or material point), the location of a particle in some configuration, a deformation, a motion, Eulerian and Lagrangian descriptions of a physical quantity, Eulerian and Lagrangian spatial derivatives, and Eulerian and Lagrangian time derivatives (including the material time derivative).
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5525571505420
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
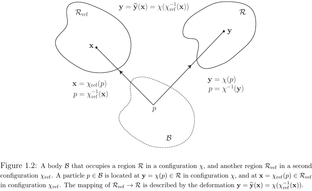
Open itWe shall use the term “body” to be a mathematical abstraction of an “object that occurs in nature”. A body \(\mathcal B\) is composed of a set of particles \(p\) (or material points). In a given configuration of the body, each particle is located at some definite point \(\mathbf{y}\) in three-dimensional space. The set of all the points in space, corresponding to the locations of all the particles, is the region \(\mathcal R\) occupied by the body in that configuration. A particular body, composed of a particular set of particles, can adopt different configurations under the action of different stimuli (forces, heating etc.) and therefore occupy different regions of space under different conditions. Note the distinction between the body, a configuration of the body, and the region the body occupies in that configuration; we make these distinctions rigorous in what follows. Similarly note the distinction between a particle and the position in space it occupies in some configuration. In order to appreciate the difference between a configuration and the region occupied in that configuration, consider the following example: suppose that a body, in a certain configuration, occupies a circular cylindrical region of space. If the object is “twisted” about its axis (as in torsion), it continues to occupy this same (circular cylindrical) region of space. Thus the region occupied by the body has not changed even though we would say that the body is in a different “configuration”.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5525573864716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itMore formally, in continuum mechanics a body \(\mathcal B\) is a collection of elements which can be put into one-to-one correspondence with some region \(\mathcal R\) of Euclidean point space. An element \(p \in \mathcal B\) is called a particle (or material point). Thus, given a body \(\mathcal B\), there is necessarily a mapping \(\chi\) that takes particles \(p \in \mathcal B\) into their geometric locations \(y \in \mathcal R\) in three-dimensional Euclidean space: \(y = \chi(p) \quad \textrm{where} \quad p \in \mathcal B, \mathbf{y} \in \mathcal R.\) The mapping \(\chi\) is called a configuration of the body \(\mathcal B\); \(\mathbf y\) is the position occupied by the particle \(p\) in the configuration \(\chi\); and \(\mathcal R\) is the region occupied by the body in the configuration \(\chi\). Often, we write \(\mathcal R = \chi \left( \mathcal B \right)\).
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5525576748300
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525582253324
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 5525590117644
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itel{\textrm{def}}{=} \chi \left( \chi_\textrm{ref}^{-1} \left( \mathbf x\right) \right), \qquad \mathbf x \in \mathcal R_\textrm{ref}, \mathbf y \in \mathcal R;\) \(\hat{\mathbf y}\) is called a <span>deformation of the body from the reference confinguration \( \chi_\textrm{ref}\). <span>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5525591690508
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525597195532
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525602700556
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525606632716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525610827020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525614234892
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 5525620526348
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |