Edited, memorised or added to reading queue
on 28-Aug-2020 (Fri)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 5731199618316
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 5731271183628
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSir Benjamin Brodie, however, regarded the enlarged prostate as an almost invariable accompaniment of advanced age, elegantly stating that ‘when the hair becomes grey and scanty, when specks of earthy matter begin to be deposited in the tunics of
Original toplevel document (pdf)
cannot see any pdfsFlashcard 5731274591500
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThat old men suffer with their prostates is a cliché as old as time. According to Hippocrates: ‘Diseases about the kidneys and bladder are cured with difficulty in old men’. 1 In the book of Ecclesiastes, in the Bible, old age is discussed, while writin
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 5731282193676
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itres, but no effect on urinary flow rate or PVR (55–59). Currently, daily tadalafil is the only PDE5-I that is approved by the FDA for treatment of BPH. Although these medications are expensive, <span>patients with concomitant erectile dysfunction may derive the most benefit from PDE5-I treatment for their LUTS related to BPH <span>
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Stirling's approximation - Wikipedia
Stirling's formula 7 Versions suitable for calculators 8 Estimating central effect in the binomial distribution 9 History 10 See also 11 Notes 12 References 13 External links Derivation[edit ] <span>Roughly speaking, the simplest version of Stirling's formula can be quickly obtained by approximating the sum ln n ! = ∑ j = 1 n ln j {\displaystyle \ln n!=\sum _{j=1}^{n}\ln j} with an integral : ∑ j = 1 n ln j ≈ ∫ 1 n ln x d x = n ln n − n + 1. {\displaystyle \sum _{j=1}^{n}\ln j\approx \int _{1}^{n}\ln x\,{\rm {d}}x=n\ln n-n+1.} The full formula, together with precise estimates of its error, can be derived as follows. Instead of approximating n!, one considers its natural logarithm , as this is a slowly varying
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
Wikipedia Join the WPWP Campaign to help improve Wikipedia articles with photos and win a prize Slowly varying function From Wikipedia, the free encyclopedia Jump to navigation Jump to search I<span>n real analysis, a branch of mathematics, a slowly varying function is a function of a real variable whose behaviour at infinity is in some sense similar to the behaviour of a function converging at infinity. Similarly, a regularly varying function is a function of a real variable whose behaviour at infinity is similar to the behaviour of a power law function (like a polynomial) near infinity. These classes of functions were both introduced by Jovan Karamata,[1][2] and have found several important applications, for example in probability theory. Contents 1 Basic definitions 2
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
roperties 2.1 Uniformity of the limiting behaviour 2.2 Karamata's characterization theorem 2.3 Karamata representation theorem 3 Examples 4 See also 5 Notes 6 References Basic definitions[edit] <span>Definition 1. A measurable function L : (0,+∞) → (0,+∞) is called slowly varying (at infinity) if for all a > 0, lim x → ∞ L ( a x ) L ( x ) = 1. {\displaystyle \lim _{x\to \infty }{\frac {L(ax)}{L(x)}}=1.} Definition 2. A function L : (0,+∞) → (0,+∞) for which the limit g ( a ) = lim x → ∞ L ( a x ) L ( x ) {\displaystyle g(a)=\lim _{x\to \infty }{\frac {L(ax)}{L(x)}}} is finite but nonze
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
measurable function L : (0,+∞) → (0,+∞) is called slowly varying (at infinity) if for all a > 0, lim x → ∞ L ( a x ) L ( x ) = 1. {\displaystyle \lim _{x\to \infty }{\frac {L(ax)}{L(x)}}=1.} <span>Definition 2. A function L : (0,+∞) → (0,+∞) for which the limit g ( a ) = lim x → ∞ L ( a x ) L ( x ) {\displaystyle g(a)=\lim _{x\to \infty }{\frac {L(ax)}{L(x)}}} is finite but nonzero for every a > 0, is called a regularly varying function. These definitions are due to Jovan Karamata.[1][2] Note. In the regularly varying case, the sum of two
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
measurable function L : (0,+∞) → (0,+∞) is called slowly varying (at infinity) if for all a > 0, lim x → ∞ L ( a x ) L ( x ) = 1. {\displaystyle \lim _{x\to \infty }{\frac {L(ax)}{L(x)}}=1.} <span>Definition 2. A function L : (0,+∞) → (0,+∞) for which the limit g ( a ) = lim x → ∞ L ( a x ) L ( x ) {\displaystyle g(a)=\lim _{x\to \infty }{\frac {L(ax)}{L(x)}}} is finite but nonzero for every a > 0, is called a regularly varying function. These definitions are due to Jovan Karamata.[1][2] Note. In the regularly varying case, the sum of two slowly varying functions is again slowly varying function. Basic properties[edit]
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
displaystyle g(a)=\lim _{x\to \infty }{\frac {L(ax)}{L(x)}}} is finite but nonzero for every a > 0, is called a regularly varying function. These definitions are due to Jovan Karamata.[1][2] <span>Note. In the regularly varying case, the sum of two slowly varying functions is again slowly varying function. Basic properties[edit] Regularly varying functions have some important properties:[1] a partial list of them is reported below. More extensive analyses of the properties characterizing
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Uniform convergence - Wikipedia
f N + 2 , … {\displaystyle f_{N},f_{N+1},f_{N+2},\ldots } differ from f {\displaystyle f} by no more than ϵ {\displaystyle \epsilon } at every point x {\displaystyle x} in E {\displaystyle E} . <span>Described in an informal way, if f n {\displaystyle f_{n}} converges to f {\displaystyle f} uniformly, then the rate at which f n ( x ) {\displaystyle f_{n}(x)} approaches f ( x ) {\displaystyle f(x)} is "uniform" throughout its domain in the following sense: in order to determine how large n {\displaystyle n} needs to be to guarantee that f n ( x ) {\displaystyle f_{n}(x)} falls within a certain distance ϵ {\displaystyle \epsilon } of f ( x ) {\displaystyle f(x)} , we do not need to know the value of x ∈ E {\displaystyle x\in E} in question — there is a single value of N = N ( ϵ ) {\displaystyle N=N(\epsilon )} independent of x {\displaystyle x} , such that choosing n {\displaystyle n} to be larger than N {\displaystyle N} will suffice. The difference between uniform convergence and pointwise convergence was not fully appreciated early in the history of calculus, leading to instances of faulty reasoning. The concept,
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Uniform convergence - Wikipedia
Uniform convergence - Wikipedia Uniform convergence From Wikipedia, the free encyclopedia Jump to navigation Jump to search In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions ( f n ) {\displaystyle (f_{n})} converges uniformly to a limiting function f {\displaystyle f} on a set E {\displaystyle E} if, given any arbitrarily small positive number ϵ {\displaystyle \epsilon } , a number N {\displaystyle N} can be found such that each of the functions f N , f N + 1 , f N + 2 , … {\displaystyle f_{N},f_{N+1},f_{N+2},\ldots } differ from f {\displaystyle f} by no more than ϵ {\displaystyle \epsilon } at every point x {\displaystyle x} in E {\displaystyle E} . Described in an informal way, if f n {\displaystyle f_{n}} converges to f {\displaystyle f} uniformly, then the rate at which f n ( x ) {\displaystyle f_{n}(x)} approaches f ( x ) {\dis
Flashcard 5731738062092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Power law - Wikipedia
her uses, see Power. An example power-law graph that demonstrates ranking of popularity. To the right is the long tail, and to the left are the few that dominate (also known as the 80–20 rule). <span>In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four.[1] Contents 1 Empirical examples 2 Properties 2.1 Scale invariance 2.2 Lack of well-defined average value 2.3 Universality 3 Power-law functions 3.1 Examples 3.1.1 Astronomy 3.1.2 Crimin
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Power law - Wikipedia
ds for many complex media. Allometric scaling laws for relationships between biological variables are among the best known power-law functions in nature. Properties[edit] Scale invariance[edit] <span>One attribute of power laws is their scale invariance. Given a relation f ( x ) = a x − k {\displaystyle f(x)=ax^{-k}} , scaling the argument x {\displaystyle x} by a constant factor c {\displaystyle c} causes only a proportionate scaling of the function itself. That is, f ( c x ) = a ( c x ) − k = c − k f ( x ) ∝ f ( x ) , {\displaystyle f(cx)=a(cx)^{-k}=c^{-k}f(x)\propto f(x),\!} where ∝ {\displaystyle \propto } denotes direct proportionality. That is, scaling by a constant c {\displaystyle c} simply multiplies the original power-law relation by the constant c − k {\displaystyle c^{-k}} . Thus, it follows that all power laws with a particular scaling exponent are equivalent up to constant factors, since each is simply a scaled version of the others. This behavior is what produces the linear relationship when logarithms are taken of both f ( x ) {\displaystyle f(x)} and x {\displaystyle x} , and the straight-line on the log–log plot is often called the signature of a power law. With real data, such straightness is a necessary, but not sufficient, condition for the data following a power-law relation. In fact, there are many ways to generate finite amounts of d
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
EXPERIMENT 2: Working with logarithmic scales
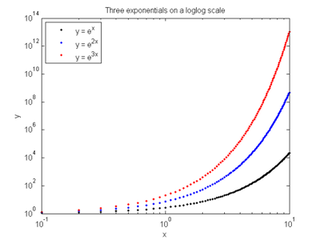
logx(x, y1, '.k', x, y2, '.b', x, y3, '.r'); title ('Three exponentials on a semilog x scale') xlabel('x'); ylabel('y'); legend({'y = e^x', 'y = e^{2x}', 'y = e^{3x}'}, 'Location', 'Northwest') <span>plot the exponentials on a log-log scale figure loglog(x, y1, '.k', x, y2, '.b', x, y3, '.r'); title ('Three exponentials on a loglog scale') xlabel('x'); ylabel('y'); legend({'y = e^x', 'y = e^{2x}', 'y = e^{3x}'}, 'Location', 'Northwest') Experiment 2c: Behavior of logarithms when plotted using different scales Create data for 3 exponential functions for points in the interval [0.1, 10] x = 0.1:0.1:10; y1 = log(x); % Eva
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
EXPERIMENT 2: Working with logarithmic scales
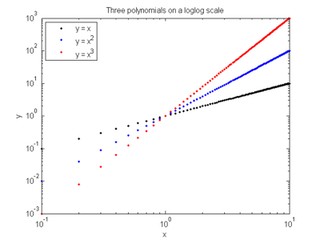
gure semilogx(x, y1, '.k', x, y2, '.b', x, y3, '.r'); title ('Three polynomials on a semilog x scale') xlabel('x'); ylabel('y'); legend({'y = x', 'y = x^2', 'y = x^3'}, 'Location', 'Northwest') <span>plot the polynomials on a log-log scale figure loglog(x, y1, '.k', x, y2, '.b', x, y3, '.r'); title ('Three polynomials on a loglog scale') xlabel('x'); ylabel('y'); legend({'y = x', 'y = x^2', 'y = x^3'}, 'Location', 'Northwest') Experiment 2b: Behavior of exponentials when plotted using different scales Create data for 3 exponential functions for points in the interval [0.1, 10] x = 0.1:0.1:10; y1 = exp(x); % E
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Power law - Wikipedia
-normal distribution).[citation needed] Thus, accurately fitting and validating power-law models is an active area of research in statistics; see below. Lack of well-defined average value[edit] <span>A power-law x − k {\displaystyle x^{-k}} has a well-defined mean over x ∈ [ 1 , ∞ ) {\displaystyle x\in [1,\infty )} only if k > 2 {\displaystyle k>2} , and it has a finite variance only if k > 3 {\displaystyle k>3} ; most identified power laws in nature have exponents such that the mean is well-defined but the variance is not, implying they are capable of black swan behavior.[2] This can be seen in the following thought experiment:[10] imagine a room with your friends and estimate the average monthly income in the room. Now imagine the world's richest perso
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Black swan theory - Wikipedia
wan theory - Wikipedia Black swan theory From Wikipedia, the free encyclopedia Jump to navigation Jump to search Theory of response to surprise events A black swan (Cygnus atratus) in Australia <span>The black swan theory or theory of black swan events is a metaphor that describes an event that comes as a surprise, has a major effect, and is often inappropriately rationalised after the fact with the benefit of hindsight. The term is based on an ancient saying that presumed black swans did not exist – a saying that became reinterpreted to teach a different lesson after the first European encounter with t
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Pointwise convergence - Wikipedia
\lim _{n\rightarrow \infty }f_{n}(x)=f(x)} for every x in the domain. The function f {\displaystyle f} is said to be the pointwise limit function of f n {\displaystyle f_{n}} . Properties[edit] <span>This concept is often contrasted with uniform convergence. To say that lim n → ∞ f n = f uniformly {\displaystyle \lim _{n\rightarrow \infty }f_{n}=f\ {\mbox{uniformly}}} means that lim n → ∞ sup { | f n ( x ) − f ( x ) | : x ∈ A } = 0 , {\displaystyle \lim _{n\rightarrow \infty }\,\sup\{\,\left|f_{n}(x)-f(x)\right|:x\in A\,\}=0,} where A {\displaystyle A} is the common domain of f {\displaystyle f} and f n {\displaystyle f_{n}} . That is a stronger statement than the assertion of pointwise convergence: every uniformly convergent sequence is pointwise convergent, to the same limiting function, but some pointwise convergent sequences are not uniformly convergent. For example, if f n : [ 0 , 1 ) → [ 0 , 1 ) {\displaystyle f_{n}:[0,1)\rightarrow [0,1)} is a sequence of functions defined by f n ( x ) = x n {\displaystyle f_{n}(x)=x^{n}} , then lim n → ∞ f n ( x ) = 0 {\displaystyle \lim _{n\rightarrow \infty }f_{n}(x)=0} pointwise on the interval [0,1), but not uniformly. The pointwise limit of a sequence of continuous functions may be a discontinuous function, but only if the convergence is not uniform. For example, f ( x ) = lim n → ∞ cos ( π x ) 2 n
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Pointwise convergence - Wikipedia
n[edit] Suppose ( f n ) {\displaystyle (f_{n})} is a sequence of functions sharing the same domain and codomain. The codomain is most commonly the reals, but in general can be any metric space. <span>The sequence ( f n ) {\displaystyle (f_{n})} converges pointwise to the function f {\displaystyle f} , often written as lim n → ∞ f n = f pointwise , {\displaystyle \lim _{n\rightarrow \infty }f_{n}=f\ {\mbox{pointwise}},} if and only if lim n → ∞ f n ( x ) = f ( x ) {\displaystyle \lim _{n\rightarrow \infty }f_{n}(x)=f(x)} for every x in the domain. The function f {\displaystyle f} is said to be the pointwise limit function of f n {\displaystyle f_{n}} . Properties[edit] This concept is often contrasted with uniform convergence. To say that lim n → ∞ f n = f uniformly {\displaystyle \lim _{n\rightarrow \infty }f_{n}=f\ {\mbox{uniformly}
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Slowly varying function - Wikipedia
unction. These definitions are due to Jovan Karamata.[1][2] Note. In the regularly varying case, the sum of two slowly varying functions is again slowly varying function. Basic properties[edit] <span>Regularly varying functions have some important properties:[1] a partial list of them is reported below. More extensive analyses of the properties characterizing regular variation are presented in the monograph by Bingham, Goldie & Teugels (1987). Uniformity of the limiting behaviour[edit] Theorem 1. The limit in definitions 1 and 2 is uniform if a is restricted to a compact interval. Karamata's characterization theorem[edit] Theorem 2. Every regularly varying function f : (0,+∞) → (0,+∞) is of the form f ( x ) = x β L ( x ) {\displaystyle f(x)=x^{\beta }L(x)} where
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
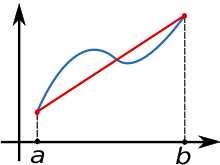
Trapezoidal rule - Wikipedia
ule (differential equations). For the explicit trapezoidal rule for solving initial value problems, see Heun's method. The function f(x) (in blue) is approximated by a linear function (in red). <span>In mathematics, and more specifically in numerical analysis, the trapezoidal rule (also known as the trapezoid rule or trapezium rule) is a technique for approximating the definite integral. ∫ a b f ( x ) d x {\displaystyle \int _{a}^{b}f(x)\,dx} . The trapezoidal rule works by approximating the region under the graph of the function f ( x ) {\displaystyle f(x)} as a trapezoid and calculating its area. It follows that ∫ a b f ( x ) d x ≈ ( b − a ) ⋅ f ( a ) + f ( b ) 2 {\displaystyle \int _{a}^{b}f(x)\,dx\approx (b-a)\cdot {\tfrac {f(a)+f(b)}{2}}} . The trapezoidal rule may be viewed as the result obtained by averaging the left and right Riemann sums, and is sometimes defined this way. The integral can be even better approximated b
Flashcard 5731771616524
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open it\({\displaystyle \int _{a}^{b}f(x)\,dx}\). The trapezoidal rule works by approximating the region under the graph of the function \(f(x)\) as a trapezoid and calculating its area. It follows th<span>at \({\displaystyle \int _{a}^{b}f(x)\,dx\approx (b-a)\cdot {\tfrac {f(a)+f(b)}{2}}}\). <span>
Original toplevel document
Trapezoidal rule - Wikipediaule (differential equations). For the explicit trapezoidal rule for solving initial value problems, see Heun's method. The function f(x) (in blue) is approximated by a linear function (in red). <span>In mathematics, and more specifically in numerical analysis, the trapezoidal rule (also known as the trapezoid rule or trapezium rule) is a technique for approximating the definite integral. ∫ a b f ( x ) d x {\displaystyle \int _{a}^{b}f(x)\,dx} . The trapezoidal rule works by approximating the region under the graph of the function f ( x ) {\displaystyle f(x)} as a trapezoid and calculating its area. It follows that ∫ a b f ( x ) d x ≈ ( b − a ) ⋅ f ( a ) + f ( b ) 2 {\displaystyle \int _{a}^{b}f(x)\,dx\approx (b-a)\cdot {\tfrac {f(a)+f(b)}{2}}} . The trapezoidal rule may be viewed as the result obtained by averaging the left and right Riemann sums, and is sometimes defined this way. The integral can be even better approximated b
Flashcard 5731776335116
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Inversion: The Power of Avoiding Stupidity
about them forwards and backward. Inversion often forces you to uncover hidden beliefs about the problem you are trying to solve. “Indeed,” says Munger, “many problems can’t be solved forward.” <span>Let’s take a look at some examples. Say you want to improve innovation in your organization. Thinking forward, you’d think about all of the things you could do to foster innovation. If you look at the problem by inversion, however, you’d think about all the things you could do that would discourage innovation. Ideally, you’d avoid those things. Sounds simple right? I bet your organization does some of those ‘stupid’ things today. Another example, rather than think about what makes a good life, you can think about what prescriptions would ensure misery. Avoiding stupidity is easier than seeking brilliance. While
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Inversion: The Power of Avoiding Stupidity
ty Inversion and The Power of Avoiding Stupidity Reading Time: 2 minutes Charlie Munger, the business partner of Warren Buffett and Vice Chairman of Berkshire Hathaway, is famous for his quote “<span>All I want to know is where I’m going to die, so I’ll never go there.” That thinking was inspired by the German mathematician Carl Gustav Jacob Jacobi, famous for some work on elliptic functions that I’ll never understand. Jacobi often solved difficult p
Flashcard 5731788655884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAll I want to know is where I’m going to die, so I’ll never go there
Original toplevel document
Inversion: The Power of Avoiding Stupidityty Inversion and The Power of Avoiding Stupidity Reading Time: 2 minutes Charlie Munger, the business partner of Warren Buffett and Vice Chairman of Berkshire Hathaway, is famous for his quote “<span>All I want to know is where I’m going to die, so I’ll never go there.” That thinking was inspired by the German mathematician Carl Gustav Jacob Jacobi, famous for some work on elliptic functions that I’ll never understand. Jacobi often solved difficult p