on 30-Sep-2022 (Fri)

Mayer studied to become a medical doctor (his studies included one physics course) and in 1840, at age 25, he signed on as a ship’s doctor on a ship bound for the tropics. Shortly after reaching the Dutch East Indies, some of the sailors became ill and Mayer’s treatment included blood letting. He was amazed to find that the venous blood was a bright red, almost the same as arterial blood. Back in Germany, the venous blood was much darker, and there was a reason: the chemist Lavoisier had explained that the body’s use of food, at least in part, amounted to burning it in a controlled way to supply warmth. The darker venous blood in effect contained the ashes, to be delivered to the lungs and expelled as carbon dioxide. Mayer concluded that less burning of food was needed to keep warm in the tropics, hence the less dark blood.

Now, Lavoisier had claimed that the amount of heat generated by burning, or oxygenation, of a certain amount of carbon did not depend on the sequence of chemical reactions involved, so the heat generated by blood chemistry oxygenation would be the same as that from uncontrolled old-fashioned burning in air. This quantitative formulation led Mayer to think about how he would measure the heat generated in the body, to equate it to the food burned. But this soon led to a problem. Anyone can generate extra heat, just by rubbing the hands together, or, for example, by turning a rusty, unoiled wheel: the axle will get hot. Does this ‘outside’ heat also count as generated by the food? Presumably yes, the food powers the body, and the body generates the heat, even if indirectly. Mayer was convinced from his childhood experience with the water wheel that nothing came from nothing: that outside heat could not just appear from nowhere, it had to have a cause.

But he saw that if the indirectly generated heat must also be included, there is a problem. His analysis ran something like this (I’ve changed the illustration slightly, but the idea’s the same): suppose two people are each steadily turning large wheels at the same rate, and the wheels are equally hard to turn. One of them is our rusty unoiled wheel from the last paragraph, and all that person’s efforts are going into generating heat. But the other wheel has a smooth, oiled axle and generates a negligible amount of heat. It is equally hard to turn, though, because it is raising a large bucket of water from a deep well. How do we balance the ‘food = heat’ budget in this second case?

Mayer was forced to the conclusion that for the ‘food = heat’ equation to make sense, there had to be another equivalence: a certain amount of mechanical work, measured for example by raising a known weight through a given distance, had to count the same as a certain amount of heat, measured by raising the temperature of a fixed amount of water, say, a certain number of degrees. In modern terms, a joule has to be equivalent to a fixed number of calories.

The first step on the road to a thermometer was taken by one Philo of Byzantium , an engineer, in the second century BC. He took a hollow lead sphere connected with a tight seal to one end of a pipe, the other end of the pipe being under water in another vessel.

To quote Philo: “…if you expose the sphere to the sun, part of the air enclosed in the tube will pass out when the sphere becomes hot. This will be evident because the air will descend from the tube into the water, agitating it and producing a succession of bubbles.

Now if the sphere is put back in the shade, that is, where the sun’s rays do not reach it, the water will rise and pass through the tube …”

“No matter how many times you repeat the operation, the same thing will happen.

In fact, if you heat the sphere with fire, or even if you pour hot water over it, the result will be the same.”

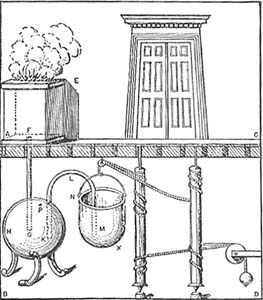
Some Classic Dramatic Uses of Temperature-Dependent Effects

This expansion of air on heating became widely known in classical times, and was used in various dramatic devices. For example, Hero of Alexandria describes a small temple where a fire on the altar causes the doors to open.

The altar is a large airtight box, with a pipe leading from it to another enclosed container filled with water. When the fire is set on top of the altar, the air in the box heats up and expands into a second container which is filled with water. This water is forced out through an overflow pipe into a bucket hung on a rope attached to the door hinges in such a way that as the bucket fills with water, it drops, turns the hinges, and opens the doors. The pipe into this bucket reaches almost to the bottom, so that when the altar fire goes out, the water is sucked back and the doors close again. (Presumably, once the fire is burning, the god behind the doors is ready to do business and the doors open…)

He first heated the bulb with his hands then immediately put it into water. He recorded that the water rose in the bulb the height of “one palm”. Later, either Galileo or his colleague Santorio Santorio put a paper scale next to the tube to read off changes in the water level. This definitely made it a thermometer, but who thought of it first isn’t clear (they argued about it). And, in fact, this thermometer had problems.

Question : what problems? If you occasionally top up the water, why shouldn’t this thermometer be good for recording daily changes in temperature?

Answer : because it’s also a barometer! But—Galileo didn’t know about the atmospheric pressure.

Torricelli, one of Galileo’s pupils, was the first to realize, shortly after Galileo died, that the real driving force in suction was external atmospheric pressure, a satisfying mechanical explanation in contrast to the philosophical “nature abhors a vacuum”. In the 1640’s, Pascal pointed out that the variability of atmospheric pressure rendered the air thermometer untrustworthy.

Liquid-in-glass thermometers were used from the 1630’s, and they were of course insensitive to barometric pressure. Meteorological records were kept from this time, but there was no real uniformity of temperature measurement until Fahrenheit, almost a hundred years later.

Newton tried to estimate the higher temperatures indirectly. He heated up a piece of iron in a fire, then let it cool in a steady breeze. He found that, at least at the lower temperatures where he could cross check with his thermometer, the temperature dropped in a geometric progression, that is, if it took five minutes to drop from 80 ° above air temperature to 40 ° above air temperature, it took another five minutes to drop to 20 ° above air, another five to drop to 10 ° above, and so on. He then assumed this same pattern of temperature drop was true at the high temperatures beyond the reach of his thermometer, and so estimated the temperature of the fire and of iron glowing red hot. This wasn’t very accurate—he (under)estimated the temperature of the fire to be about 600 ° C.

Project scoping for ML is incredibly challenging. Even for the most seasoned ML veterans, conjecturing how long a project will take, which approach is going to be most successful, and the amount of resources required is a futile and frustrating exercise. The risk associated with making erroneous claims is fairly high, but structuring proper scoping and solution research can help minimize the chances of being wildly off on estimation.

Most companies have a mix of the types of people in this hyperbolic scenario. Some are academics whose sole goal is to further the advancement of knowledge and research into algorithms, paving the way for future discoveries from within the industry. Others are “applications of ML” engineers who just want to use ML as a tool to solve a business problem. It’s important to embrace and balance both aspects of these philosophies toward ML work, strike a compromise during the research and scoping phase of a project, and know that the middle ground here is the best path to trod upon to ensure that a project actually makes it to production.

Testing approaches is a Goldilocks activity; if you don’t test enough options, you’re probably not finding the best solution, while testing too many things wastes precious time. Find the middle ground.

In the experimentation phase, the largest causes of project failure are either the experimentation taking too long (testing too many things or spending too long fine- tuning an approach) or an underdeveloped prototype that is so abysmally bad that the business decides to move on to something else.

These inexperienced DS team members, performing only the most cursory of research, adapt a basic demo from a blog post. While their basic testing shows promise, they fail to thoroughly research the implementation details required for employing the model on their data. By retraining the pretrained model on only a few hundred images of two of the many thousands of products from their corpus of images, their misleading results hide the problem with their approach

No one thinks that code quality matters until it’s 4 a.m. on a Saturday, you’re 18 hours into debugging a failure, and you still haven’t fixed the bug

Having a poor development practice for ML projects can manifest itself in a multitude of ways that can completely kill a project. Though usually not as directly visible as some of the other leading causes, having a fragile and poorly designed code base and poor development practices can make a project harder to work on, easier to break in production, and far harder to improve as time goes on

With a fully modularized code base registered in Git, each of them can check out a feature branch from the master, make small edits to the modules that are part of their features, write new tests (if needed), run their tests, and submit a pull request. Once their work is complete—because of the configuration-based code and the capability of the methods in each module class to act upon the data for their project through lever- aging the job configuration—each feature branch will not impact the other and should just work as designed. Julie and Joe can cut a release branch of both of their changes in a single build, run a full integration test, and safely merge to the master, confident that their work is correct. They can, in effect, work efficiently together on the same code base, greatly minimizing the chance of errors and reducing the amount of time spent debugging code.