Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#has-images #quantitative-methods-basic-concepts #statistics
Geometric Mean
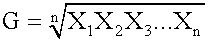
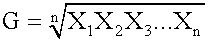
The geometric mean has three important properties:
- It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative.
- If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value.
- It is always less than the arithmetic mean if values in the data set are not equal.
It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean.
If you want to change selection, open document below and click on "Move attachment"
Subject 4. Measures of Center Tendency
owing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
Subject 4. Measures of Center Tendency
owing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.