Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#has-images
Logarithm and exponential [ edit ]
Let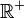 
be the multiplicative group of positive real numbers, and let 
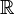be the additive group of real numbers.
The logarithm function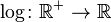 
satisfies 
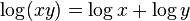for all 
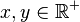, so it is a group homomorphism. The exponential function 
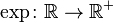satisfies 
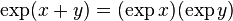for all 
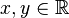, so it too is a homomorphism.
The identities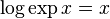 
and 
show that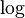 
and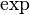 
are inverses of each other. Since 
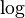is a homomorphism that has an inverse that is also a homomorphism, 
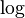is an isomorphism of groups.
Because 
is an isomorphism, it translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale.
If you want to change selection, open document below and click on "Move attachment"
Isomorphism - Wikipedia, the free encyclopedia
and exponential 1.2 Integers modulo 6 1.3 Relation-preserving isomorphism 2 Isomorphism vs. bijective morphism 3 Applications 4 Relation with equality 5 See also 6 Notes 7 References 8 Further reading 9 External links Examples[edit] <span>Logarithm and exponential[edit] Let be the multiplicative group of positive real numbers, and let be the additive group of real numbers. The logarithm function satisfies for all , so it is a group homomorphism. The exponential function satisfies for all , so it too is a homomorphism. The identities and show that and are inverses of each other. Since is a homomorphism that has an inverse that is also a homomorphism, is an isomorphism of groups. Because is an isomorphism, it translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale. Integers modulo 6[edit] Consider the group , the integers from 0 to 5 with addition modulo 6. Also consider the group , the ordered pairs where the x coordinates can be 0 or 1, and the
Isomorphism - Wikipedia, the free encyclopedia
and exponential 1.2 Integers modulo 6 1.3 Relation-preserving isomorphism 2 Isomorphism vs. bijective morphism 3 Applications 4 Relation with equality 5 See also 6 Notes 7 References 8 Further reading 9 External links Examples[edit] <span>Logarithm and exponential[edit] Let be the multiplicative group of positive real numbers, and let be the additive group of real numbers. The logarithm function satisfies for all , so it is a group homomorphism. The exponential function satisfies for all , so it too is a homomorphism. The identities and show that and are inverses of each other. Since is a homomorphism that has an inverse that is also a homomorphism, is an isomorphism of groups. Because is an isomorphism, it translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale. Integers modulo 6[edit] Consider the group , the integers from 0 to 5 with addition modulo 6. Also consider the group , the ordered pairs where the x coordinates can be 0 or 1, and the
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.