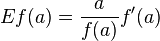Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
#calculus #elasticity #has-images #mathematics
In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives
meaning in words: It is thus the ratio of the relative (percentage) change in the function's output \(f(a)\) with respect to the relative change in its input \(a\), for infinitesimal changes from a point 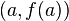 .
.
If you want to change selection, open original toplevel document below and click on "Move attachment"
In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using l
er:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
Parent (intermediate) annotation
Open itIn mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using l
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
Summary
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Details
Discussion
Do you want to join discussion? Click here to log in or create user.