Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Tags
#has-images #reading-9-probability-concepts
Question
The combination formula, or the binomial formula):
Answer
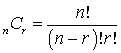
Tags
#has-images #reading-9-probability-concepts
Question
The combination formula, or the binomial formula):
Answer
?
Tags
#has-images #reading-9-probability-concepts
Question
The combination formula, or the binomial formula):
Answer
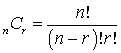
If you want to change selection, open original toplevel document below and click on "Move attachment"
A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):
nlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
Parent (intermediate) annotation
Open itA combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):
Original toplevel document
Subject 10. Principles of Countingnlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
Summary
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Details
No repetitionsDiscussion
Do you want to join discussion? Click here to log in or create user.