Do you want BuboFlash to help you learning these things? Or do you want to add or correct something? Click here to log in or create user.
Tags
#bonds #duration #finance #has-images
Question
well-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually)
[...]
where:
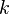is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),
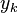is the yield to maturity for an asset, periodically compounded
Answer
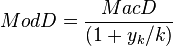
Tags
#bonds #duration #finance #has-images
Question
well-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually)
[...]
where:
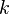- is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),
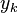- is the yield to maturity for an asset, periodically compounded
Answer
?
Tags
#bonds #duration #finance #has-images
Question
well-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually)
[...]
where:
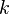- is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),
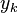- is the yield to maturity for an asset, periodically compounded
Answer
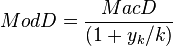
If you want to change selection, open original toplevel document below and click on "Move attachment"
well-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually): where: is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the yield to maturity for
uously compounded. Then expression (2) becomes: To find modified duration, when we take the derivative of the value with respect to the periodically compounded yield we find [5] Rearranging (dividing both sides by -V) gives: which is the <span>well-known relationship between modified duration and Macaulay duration: where: indexes the cash flows, is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the cash flow of the th payment from an asset, is the time in years until the th payment will be received (e.g. a two-year semi-annual would be represented by a index of 0.5, 1.0, 1.5, and 2.0), is the yield to maturity for an asset, periodically compounded is the present value of all cash payments from the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are clo
Parent (intermediate) annotation
Open itwell-known relationship between modified duration and Macaulay duration if yield is periodically compounded (not continually): where: is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the yield to maturity for
Original toplevel document
Bond duration - Wikipedia, the free encyclopediauously compounded. Then expression (2) becomes: To find modified duration, when we take the derivative of the value with respect to the periodically compounded yield we find [5] Rearranging (dividing both sides by -V) gives: which is the <span>well-known relationship between modified duration and Macaulay duration: where: indexes the cash flows, is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the cash flow of the th payment from an asset, is the time in years until the th payment will be received (e.g. a two-year semi-annual would be represented by a index of 0.5, 1.0, 1.5, and 2.0), is the yield to maturity for an asset, periodically compounded is the present value of all cash payments from the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are clo
Summary
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Details
No repetitionsDiscussion
Do you want to join discussion? Click here to log in or create user.