Edited, memorised or added to reading queue
on 17-Jul-2014 (Thu)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
ty become its new market rate. Because a bond is always anchored by its final maturity, the price at some point must change direction and fall to par value at redemption. A bond's market value at different times in its life can be calculated. <span>When the yield curve is steep, the bond is predicted to have a large capital gain in the first years before falling in price later. When the yield curve is flat, the capital gain is predicted to be much less, and there is little variability in the bond's total returns over time. Rising (or falling) interest rates rar
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
nsitivity of a bond's market price to interest rate (i.e. yield) movements is measured by its duration, and, additionally, by its convexity. Duration is a linear measure of how the price of a bond changes in response to interest rate changes. <span>It is approximately equal to the percentage change in price for a given change in yield, and may be thought of as the elasticity of the bond's price with respect to discount rates. For example, for small interest rate changes, the duration is the approximate percentage by which the value of the bond will fall for a 1% per annum increase in market interest rate. S
Flashcard 149624206
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itmarket price of a 17-year bond with a duration of 7 would fall about 7% if the market interest rate increased by 1% per annum.
Original toplevel document
Bond valuation - Wikipedia, the free encyclopediaof the bond's price with respect to discount rates. For example, for small interest rate changes, the duration is the approximate percentage by which the value of the bond will fall for a 1% per annum increase in market interest rate. So the <span>market price of a 17-year bond with a duration of 7 would fall about 7% if the market interest rate (or more precisely the corresponding force of interest) increased by 1% per annum. Convexity is a measure of the "curvature" of price changes. It is needed because the price is not a linear function of the discount rate, but rather a convex function of the di
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
percentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out that <span>when the yield is expressed continuously compounded, Macaulay duration and modified duration are equal. First, consider the case of continuously compounded yields. If we take the derivative of price or present value, expression (2), with respect to the continuously compounded yield we see
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Greeks (finance) - Wikipedia, the free encyclopedia
or4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
Flashcard 149625608
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn contrast to Macaulay duration, modified duration (sometimes abbreviated MD) is a price sensitivity measure, defined as the percentage derivative of price with respect to yield.
Original toplevel document
Bond duration - Wikipedia, the free encyclopediaof the yield , not varying by term to payment. With the use of computers, both forms may be calculated but expression (3), assuming a constant yield, is more widely used because of the application to modified duration. Modified duration[edit] <span>In contrast to Macaulay duration, modified duration (sometimes abbreviated MD) is a price sensitivity measure, defined as the percentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out th
Flashcard 149625619
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itwhen the yield is continuously compounded, Macaulay duration and modified duration are equal.
Original toplevel document
Bond duration - Wikipedia, the free encyclopediapercentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out that <span>when the yield is expressed continuously compounded, Macaulay duration and modified duration are equal. First, consider the case of continuously compounded yields. If we take the derivative of price or present value, expression (2), with respect to the continuously compounded yield we see
Flashcard 149625626
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itwhen the yield is continuously compounded, Macaulay duration and modified duration are equal.
Original toplevel document
Bond duration - Wikipedia, the free encyclopediapercentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out that <span>when the yield is expressed continuously compounded, Macaulay duration and modified duration are equal. First, consider the case of continuously compounded yields. If we take the derivative of price or present value, expression (2), with respect to the continuously compounded yield we see
Flashcard 149625715
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625726
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625741
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625752
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625763
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625774
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625789
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625800
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625811
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625822
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625833
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625854
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625870
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625881
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149625984
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 149626000
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
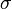 )
)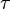 )
)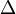
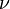
 )
) 
 )
)