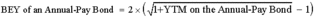Edited, memorised or added to reading queue
on 29-Mar-2016 (Tue)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
|
Bond Equivalent Yield
#has-images #quantitative-methods-basic-concepts
Periodic bond yields for both straight and zero-coupon bonds are conventionally computed based on semi-annual periods, as U.S. bonds typically make two coupon payments per year. For example, a zero-coupon bond with a maturity of five years will mature in 10 6-month periods. The periodic yield for that bond, r, is indicated by the equation Price = Maturity value x (1 + r)-10. This yield is an internal rate of return with semi-annual compounding. How do we annualize it?The convention is to double it and call the result the bond's yield to maturity. This method ignores the effect of compounding semi-annual YTM, and the YTM calculated in this way is called a bond-equivalent yield (BEY). However, yields of a semi-annual-pay and an annual-pay bond cannot be compared directly without conversion. This conversion can be done in one of the two ways:
Example
Solution 1
Solution 2
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
Subject 2. Measurement Scales
#analyst-notes #quantitative-methods-basic-concepts #statistics
Measurement is the assignment of numbers to objects or events in a systematic fashion. To choose the appropriate statistical methods for summarizing and analyzing data, we need to distinguish between different measurement scales or levels of measurement.
Note that as you move down t... |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
Subject 3. Frequency Distribution
#has-images #quantitative-methods-basic-concepts #statistics
Very often, the data available is vast, leading to a situation where dealing with individual numbers becomes laborious and messy. In such circumstances, it is neater and more convenient to summarize results into what is known as a frequency table. The data in the display is called a frequency distribution.
An interval, also called a class, is a set of values within which an observation falls.
A frequency distribution is a tabular display of data categorized into a small number of non-overlapping intervals. Note that:
It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percentage of scores in each interval are displayed. This helps in the analysis of large amount of statistical data, and works with all types of measurement scales.
The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution.
Data can be divided into two types: discrete and continuous.
There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distribution. It is constructed as follows:
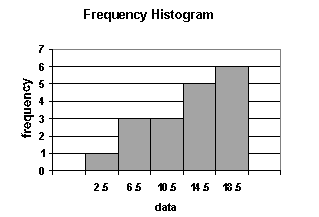 |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
|
A book on Mythology must draw from widely different sources.
|
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |