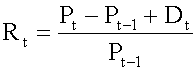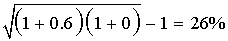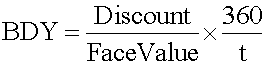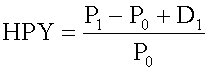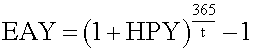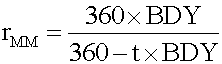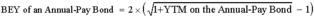Edited, memorised or added to reading queue
on 15-Jul-2017 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1428167200012
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itWe first analyze demand. The quantity consumers are willing to buy clearly depends on a number of different factors called variables. Perhaps the most important of those variables is the item’s own price.
Original toplevel document
3.1. The Demand Function and the Demand CurveWe first analyze demand. The quantity consumers are willing to buy clearly depends on a number of different factors called variables. Perhaps the most important of those variables is the item’s own price. In general, economists believe that as the price of a good rises, buyers will choose to buy less of it, and as its price falls, they buy more. This is such a ubiquitous observation that
Flashcard 1432870325516
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itVisual=spatial, e.g. patterns and designs, painting, drawing, active imagination, sculpture, colour schemes.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1443051212044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itReading 24 in study session 7 explores the roles of financial reporting standard-setting bodies and regulatory authorities. The International Accounting Standards Board’s conceptual framework and the movement towards global convergence of financial reporting standards are also described.
Original toplevel document
An Introductionnd accounting accruals. The presentation of financial information to the public by a company must conform to applicable financial reporting standards based on factors such as the jurisdiction in which the information is released. <span>The final reading in this study session explores the roles of financial reporting standard-setting bodies and regulatory authorities. The International Accounting Standards Board’s conceptual framework and the movement towards global convergence of financial reporting standards are also described. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1634597997836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1634599832844
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1634610318604
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Teoria della relatività - Wikipedia
l'enciclopedia libera. Vai a: navigazione, ricerca [imagelink] Disambiguazione – "Relatività" rimanda qui. Se stai cercando il principio di relatività, vedi Principio di relatività. <span>In fisica con teoria della relatività si intendono in generale le trasformazioni matematiche che devono essere applicate alle descrizioni dei fenomeni fisici nel passaggio tra due sistemi di riferimento in moto relativo tra loro, secondo il principio di relatività. L'espressione è usata anche nel linguaggio comune per riferirsi alle teorie della relatività ristretta o della relatività generale di Einstein, in quanto esempi più noti del principio
l'enciclopedia libera. Vai a: navigazione, ricerca [imagelink] Disambiguazione – "Relatività" rimanda qui. Se stai cercando il principio di relatività, vedi Principio di relatività. <span>In fisica con teoria della relatività si intendono in generale le trasformazioni matematiche che devono essere applicate alle descrizioni dei fenomeni fisici nel passaggio tra due sistemi di riferimento in moto relativo tra loro, secondo il principio di relatività. L'espressione è usata anche nel linguaggio comune per riferirsi alle teorie della relatività ristretta o della relatività generale di Einstein, in quanto esempi più noti del principio
Flashcard 1634613202188
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Teoria della relatività - Wikipedia
l'enciclopedia libera. Vai a: navigazione, ricerca [imagelink] Disambiguazione – "Relatività" rimanda qui. Se stai cercando il principio di relatività, vedi Principio di relatività. <span>In fisica con teoria della relatività si intendono in generale le trasformazioni matematiche che devono essere applicate alle descrizioni dei fenomeni fisici nel passaggio tra due sistemi di riferimento in moto relativo tra loro, secondo il principio di relatività. L'espressione è usata anche nel linguaggio comune per riferirsi alle teorie della relatività ristretta o della relatività generale di Einstein, in quanto esempi più noti del principio
l'enciclopedia libera. Vai a: navigazione, ricerca [imagelink] Disambiguazione – "Relatività" rimanda qui. Se stai cercando il principio di relatività, vedi Principio di relatività. <span>In fisica con teoria della relatività si intendono in generale le trasformazioni matematiche che devono essere applicate alle descrizioni dei fenomeni fisici nel passaggio tra due sistemi di riferimento in moto relativo tra loro, secondo il principio di relatività. L'espressione è usata anche nel linguaggio comune per riferirsi alle teorie della relatività ristretta o della relatività generale di Einstein, in quanto esempi più noti del principio
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1634645445900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
#13; Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield. <span>The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Open it
The money-weighted rate of return has a serious drawback. Generally, clients determine when money is given to the investment manager and those decisions may significantly influence the money-weighted rate of return . A general principle of evaluation, however, is that a person or entity should be judged only on the basis of their own actions, or actions under their control. An evaluation tool should