Edited, memorised or added to reading queue
on 17-Jun-2018 (Sun)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
metric (SI) units 7016308570000000000♠3.0857×10 16 m ~31 petametres imperial & US units 7016308575618560000♠1.9174×10 13 mi astronomical units 7016308568047999355♠2.06265×10 5 au 7016308567400801506♠3.26156 ly <span>The parsec (symbol: pc) is a unit of length used to measure large distances to astronomical objects outside the Solar System. A parsec is defined as the distance at which one astronomical unit subtends an angle of one arcsecond, [1] which corresponds to 7005648000000000000♠648000/π astronomical units. One pa
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
0♠1.9174×10 13 mi astronomical units 7016308568047999355♠2.06265×10 5 au 7016308567400801506♠3.26156 ly The parsec (symbol: pc) is a unit of length used to measure large distances to astronomical objects outside the Solar System. <span>A parsec is defined as the distance at which one astronomical unit subtends an angle of one arcsecond, [1] which corresponds to 7005648000000000000♠648000/π astronomical units. One parsec is equal to about 3.26 light-years (30 trillion km or 19 trillion miles) in length. The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
arge distances to astronomical objects outside the Solar System. A parsec is defined as the distance at which one astronomical unit subtends an angle of one arcsecond, [1] which corresponds to 7005648000000000000♠648000/π astronomical units. <span>One parsec is equal to about 3.26 light-years (30 trillion km or 19 trillion miles) in length. The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun. [2] Most of the stars visible to the unaided eye in the night sky are within 500 parsecs of the
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
tance at which one astronomical unit subtends an angle of one arcsecond, [1] which corresponds to 7005648000000000000♠648000/π astronomical units. One parsec is equal to about 3.26 light-years (30 trillion km or 19 trillion miles) in length. <span>The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun. [2] Most of the stars visible to the unaided eye in the night sky are within 500 parsecs of the Sun. [citation needed] The parsec unit was probably first suggested in 1913 by the British
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
s to 7005648000000000000♠648000/π astronomical units. One parsec is equal to about 3.26 light-years (30 trillion km or 19 trillion miles) in length. The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun. [2] <span>Most of the stars visible to the unaided eye in the night sky are within 500 parsecs of the Sun. [citation needed] The parsec unit was probably first suggested in 1913 by the British astronomer Herbert Hall Turner. [3] Named as a portmanteau of the parallax of one arcsecond, it was defined so as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
) from the Sun. [2] Most of the stars visible to the unaided eye in the night sky are within 500 parsecs of the Sun. [citation needed] The parsec unit was probably first suggested in 1913 by the British astronomer Herbert Hall Turner. [3] <span>Named as a portmanteau of the parallax of one arcsecond, it was defined so as to make calculations of astronomical distances quick and easy for astronomers from only their raw observational data. Partly for this reason, it is the unit prefer
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
ided eye in the night sky are within 500 parsecs of the Sun. [citation needed] The parsec unit was probably first suggested in 1913 by the British astronomer Herbert Hall Turner. [3] Named as a portmanteau of the parallax of one arcsecond, <span>it was defined so as to make calculations of astronomical distances quick and easy for astronomers from only their raw observational data. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are u
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
r distances were undertaken by German astronomer Friedrich Wilhelm Bessel in 1838, who used this approach to calculate the 3.5-parsec distance of 61 Cygni. [7] [imagelink] [emptylink] stellar parallax motion from annual parallax <span>The parallax of a star is defined as half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. Equivalently, it is the subtended angle, from that star's perspective, of the semimajor axis of the Earth's orbit. The star, the Sun and the Earth form the corners of an imaginary right
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
ni. [7] [imagelink] [emptylink] stellar parallax motion from annual parallax The parallax of a star is defined as half of the angular distance that a star appears to move relative to the celestial sphere as Earth orbits the Sun. <span>Equivalently, it is the subtended angle, from that star's perspective, of the semimajor axis of the Earth's orbit. The star, the Sun and the Earth form the corners of an imaginary right triangle in space: the right angle is the corner at the Sun, and the corner at the star is the parallax angle. The length of the opposite side to the parallax angle is the distance from the Earth to the Sun (defined as one astronomical unit (au), and the length of the adjacent side gives the distance from the sun to the star. Therefore, given a measurement of the parallax angle, along with the rules of trigonometry, the distance from the Sun to the star can be found. A parsec is defined as the length of the side adjacent to the vertex occupied by a star whose parallax angle is one arcsecond. The use of the parsec as a unit of distance follows naturally from Bessel's method, because the distance in parsecs can be computed simply as the reciprocal of the parallax angle in a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
he star can be found. A parsec is defined as the length of the side adjacent to the vertex occupied by a star whose parallax angle is one arcsecond. The use of the parsec as a unit of distance follows naturally from Bessel's method, because <span>the distance in parsecs can be computed simply as the reciprocal of the parallax angle in arcseconds (i.e. if the parallax angle is 1 arcsecond, the object is 1 pc from the Sun; if the parallax angle is 0.5 arcseconds, the object is 2 pc away; etc.). No trigonometric functions are required in this relationship because the very small angles involved mean that the approximate solution of the skinny triangle can be applied. Though it
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
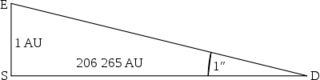
Parsec - Wikipedia
ssed his concern for the need of a name for that unit of distance. He proposed the name astron, but mentioned that Carl Charlier had suggested siriometer and Herbert Hall Turner had proposed parsec. [3] It was Turner's proposal that stuck. <span>Calculating the value of a parsec[edit] [imagelink] In the diagram above (not to scale), S represents the Sun, and E the Earth at one point in its orbit. Thus the distance ES is one astronomical unit (au). The angle SDE is one arcsecond (1/3600 of a degree) so by definition D is a point in space at a distance of one parsec from the Sun. Through trigonometry, the distance SD is calculated as follows: S D = E S tan 1 ″ {\displaystyle \mathrm {SD} ={\frac {\mathrm {ES} }{\tan 1''}}} S D ≈ E S 1 ″ = 1 au 1 60 × 60 × π 180 = 648 000 π au ≈ 206 264.81 au . {\displaystyle \mathrm {SD} \approx {\frac {\mathrm {ES} }{1''}}={\frac {1\,{\mbox{au}}}{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,{\mbox{au}}\approx 206\,264.81{\mbox{ au}}.} Because the astronomical unit is defined to be 7011149597870700000♠149597870700 m, [8] the following can be calculated: Therefore, 1 parsec ≈ 7005206264806247096♠206264.8062470
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
{\displaystyle \mathrm {SD} \approx {\frac {\mathrm {ES} }{1''}}={\frac {1\,{\mbox{au}}}{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,{\mbox{au}}\approx 206\,264.81{\mbox{ au}}.} Because <span>the astronomical unit is defined to be 7011149597870700000♠149597870700 m, [8] the following can be calculated: Therefore, 1 parsec ≈ 7005206264806247096♠206264.806247096 astronomical units ≈ 7016308567758100000♠3.085677581×10 16 metres ≈ 7001191735115770000♠1
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parsec - Wikipedia
n be calculated: Therefore, 1 parsec ≈ 7005206264806247096♠206264.806247096 astronomical units ≈ 7016308567758100000♠3.085677581×10 16 metres ≈ 7001191735115770000♠19.173511577 trillion miles ≈ 7000326156377700000♠3.261563777 light-years <span>A corollary states that a parsec is also the distance from which a disc one astronomical unit in diameter must be viewed for it to have an angular diameter of one arcsecond (by placing the observer at D and a diameter of the disc on ES). The length of the parsec used in IAU 2015 Resolution B2 [9] (exactly 7005648000000000000♠648000/π astronomical units) corresponds exactly to that derived using the small-angle calcul