Edited, memorised or added to reading queue
on 25-May-2016 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1345820691724
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Isomorphism - Wikipedia, the free encyclopedia
s article is about mathematics. For other uses, see Isomorphism (disambiguation). The group of fifth roots of unity under multiplication is isomorphic to the group of rotations of the regular pentagon under composition. <span>In mathematics, an isomorphism (from the Ancient Greek: ἴσος isos "equal", and μορφή morphe "form" or "shape") is a homomorphism or morphism (i.e. a mathematical mapping) that admits an inverse. [note 1] Two mathematical objects are isomorphic if an isomorphism exists between them. An automorphism is an isomorphism whose source and target coincide. The interest of isomorphisms lies in the fact that two isomorphic objects cannot be distinguished by using only the properties used to define morphisms; thus isomorphic objects may be considered the same as long as one considers only these properties and their consequences. For most algebraic structures, including groups and rings, a homomorphism is an isomorphism if and only if it is bijective. In topology, where the morphisms are continuous functions, isomorphisms are also called homeomorphisms or bicontinuous functions. In mathematical analysis, where the morphisms are differentiable functions, isomorphisms are also called diffeomorphisms. A canonical isomorphism is a canonical map that is an isomorphism. Two objects are said to be canonically isomorphic if there is a canonical isomorphism between them. For example, the canonical map from a finite-dimensional vector space V to its second dual space is a canonical isomorphism; on the other hand, V is isomorphic to its dual space but not canonically in general. Isomorphisms are formalized using category theory. A morphism f : X → Y in a category is an isomorphism if it admits a two-sided inverse, meaning that there is another morphism g : Y → X in that category such that gf = 1 X and fg = 1 Y , where 1 X and 1 Y are the identity morphisms of X and Y, respectively. [1] Contents 1 Examples 1.1 Logarithm and exponential 1.2 Integers modulo 6 1.3 Relation-preserving isomorphism 2 Isomorphism vs. bijective morphism 3 Applications 4 Relation with equ
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Isomorphism - Wikipedia, the free encyclopedia
and exponential 1.2 Integers modulo 6 1.3 Relation-preserving isomorphism 2 Isomorphism vs. bijective morphism 3 Applications 4 Relation with equality 5 See also 6 Notes 7 References 8 Further reading 9 External links Examples[edit] <span>Logarithm and exponential[edit] Let be the multiplicative group of positive real numbers, and let be the additive group of real numbers. The logarithm function satisfies for all , so it is a group homomorphism. The exponential function satisfies for all , so it too is a homomorphism. The identities and show that and are inverses of each other. Since is a homomorphism that has an inverse that is also a homomorphism, is an isomorphism of groups. Because is an isomorphism, it translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale. Integers modulo 6[edit] Consider the group , the integers from 0 to 5 with addition modulo 6. Also consider the group , the ordered pairs where the x coordinates can be 0 or 1, and the
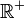 be the multiplicative group of
be the multiplicative group of 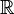 be the additive group of real numbers.
be the additive group of real numbers.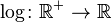 satisfies
satisfies 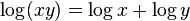 for all
for all 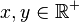 , so it is a
, so it is a 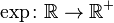 satisfies
satisfies 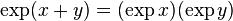 for all
for all 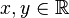 , so it too is a homomorphism.
, so it too is a homomorphism.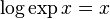 and
and 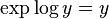 show that
show that  and
and  are
are 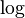 is a homomorphism that has an inverse that is also a homomorphism,
is a homomorphism that has an inverse that is also a homomorphism, 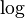 is an isomorphism of groups.
is an isomorphism of groups.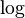 is an isomorp
is an isomorp