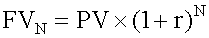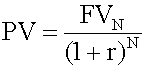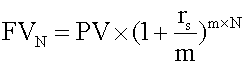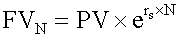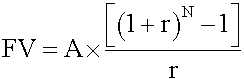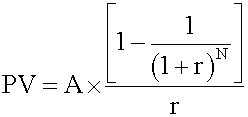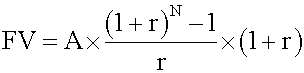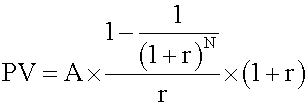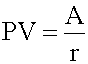Edited, memorised or added to reading queue
on 10-Jul-2017 (Mon)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1623578250508
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1624091004172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe present value of a perpetuity is A/r, where A is the periodic payment to be received forever.
Original toplevel document
Open itmay be handled in a similar fashion as single payments if we use annuity factors instead of single-payment factors. The present value, PV, is the future value, FV, times the present value factor, (1 + r) − N . <span>The present value of a perpetuity is A/r, where A is the periodic payment to be received forever. It is possible to calculate an unknown variable, given the other relevant variables in time value of money problems. The cash flow additivity principle c
Flashcard 1624656448780
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1624658283788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1624660380940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1625071684876
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
When you make a single investment today, its future value, received N years from now, is as follows: FV = future value at time n PV = present value r = interest rate per period N = number of years A key assumption of the future valu
Flashcard 1625074044172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
make a single investment today, its future value, received N years from now, is as follows: FV = future value at time n PV = present value r = interest rate per period N = number of years <span>A key assumption of the future value formula is that interim interest earned is reinvested at the given interest rate (r). This is known as compounding. In order to receive a single future cash flow N years from now, you must make an investment today in the following amount:
Flashcard 1625076403468
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
e n PV = present value r = interest rate per period N = number of years A key assumption of the future value formula is that interim interest earned is reinvested at the given interest rate (r). This is known as compounding. <span>In order to receive a single future cash flow N years from now, you must make an investment today in the following amount: Notice that the future cash flow is discounted back to the present. Therefore, the interest rate is called the discount rate. You sh
Flashcard 1625078762764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
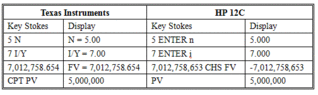
ulator keys to press are: If you are given the FV and need to solve for PV, the calculator keys to press are: When compounding periods are not annual <span>Some investments pay interest more than once a year. When you calculate these amounts, make sure that periodic interest rates correspond to the number of compounding periods in the year. For example, if time periods are quoted in quarters, quarterly interest rates should be used. When compounding periods are other than annual 
Flashcard 1625081122060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
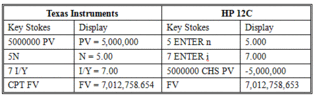
. When you calculate these amounts, make sure that periodic interest rates correspond to the number of compounding periods in the year. For example, if time periods are quoted in quarters, quarterly interest rates should be used. <span>When compounding periods are other than annual r s = the quoted annual interest rate m = the number of compounding periods per year N = the number of years. Example 2 An analyst invests $5 million in a 5-year certificate of deposit (CD) at a local financial institution. The CD promises to pay 7% per year, compounded semi-a
Flashcard 1625083481356
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
. When you calculate these amounts, make sure that periodic interest rates correspond to the number of compounding periods in the year. For example, if time periods are quoted in quarters, quarterly interest rates should be used. <span>When compounding periods are other than annual r s = the quoted annual interest rate m = the number of compounding periods per year N = the number of years. Example 2 An analyst invests $5 million in a 5-year certificate of deposit (CD) at a local financial institution. The CD promises to pay 7% per year, compounded semi-a
Flashcard 1625087413516
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
subject 3. The Future Value and Present Value of a Single Cash Flow
t? The calculator keys to press are: Note that the answer is greater than when the compounding was annual. This is because interest is earned twice a year instead of only once. <span>If the number of compounding periods becomes infinite, interest is compounding continuously. Accordingly, the future value N years from now is computed as follows: <span><body><html>
Flashcard 1625097374988
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1625099209996
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1625101045004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1625113627916
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
Annuity is a finite set of sequential cash flows, all with the same value. Ordinary annuity has a first cash flow that occurs one period from now (indexed at t = 1). In other words, the payments occur at the end of each period. Future value
Flashcard 1625115987212
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
ity is a finite set of sequential cash flows, all with the same value. Ordinary annuity has a first cash flow that occurs one period from now (indexed at t = 1). In other words, the payments occur at the end of each period. <span>Future value of a regular annuity where A = annuity amount N = number of regular annuity payments r = interest rate per period Present valu
Flashcard 1625118346508
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
he end of each period. Future value of a regular annuity where A = annuity amount N = number of regular annuity payments r = interest rate per period <span>Present value of a regular annuity Annuity due has a first cash flow that is paid immediately (indexed at t = 0). In other words, the payments occur at the beginning of
Flashcard 1625120705804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
sent value of a regular annuity Annuity due has a first cash flow that is paid immediately (indexed at t = 0). In other words, the payments occur at the beginning of each period. <span>Future value of an annuity due This consists of two parts: the future value of one annuity payment now, and the future value of a regular annuity of (N -1) period. Calculate the two parts and add them together. Alternatively, you can use this formula: Note that, all other factors being equal, the future value of an annuity due is equal to the future value of an ordinary annuity multiplied by
Flashcard 1625123065100
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
sent value of a regular annuity Annuity due has a first cash flow that is paid immediately (indexed at t = 0). In other words, the payments occur at the beginning of each period. <span>Future value of an annuity due This consists of two parts: the future value of one annuity payment now, and the future value of a regular annuity of (N -1) period. Calculate the two parts and add them together. Alternatively, you can use this formula: Note that, all other factors being equal, the future value of an annuity due is equal to the future value of an ordinary annuity multiplied by
Flashcard 1625124900108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
future value of one annuity payment now, and the future value of a regular annuity of (N -1) period. Calculate the two parts and add them together. Alternatively, you can use this formula: Note that, <span>all other factors being equal, the future value of an annuity due is equal to the future value of an ordinary annuity multiplied by (1 + r). Present value of an annuity due This consists of two parts: an annuity payment now and the present value of a regular annuity of (N - 1) period. Use the a
Flashcard 1625127259404
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
u can use this formula: Note that, all other factors being equal, the future value of an annuity due is equal to the future value of an ordinary annuity multiplied by (1 + r). <span>Present value of an annuity due This consists of two parts: an annuity payment now and the present value of a regular annuity of (N - 1) period. Use the above formula to calculate the second part and add the two parts together. This process can also be simplified to a formula: Note that, all other factors being equal, the present value of an annuity due is equal to the present value of an ordinary annuity multiplied
Flashcard 1625129618700
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. The Future Value and Present Value of a Series of Equal Cash Flows (Ordinary Annuities, Annuity Dues, and Perpetuities)
e present value of a regular annuity of (N - 1) period. Use the above formula to calculate the second part and add the two parts together. This process can also be simplified to a formula: Note that, <span>all other factors being equal, the present value of an annuity due is equal to the present value of an ordinary annuity multiplied by (1 + r). Hint: Remember these formulas - you can use them to solve annuity-related questions directly, or to double-check the answers given by your calculator. A perpe