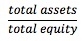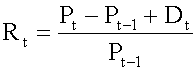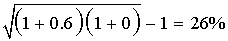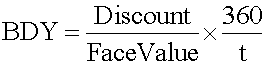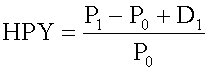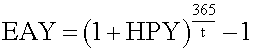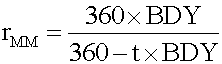Edited, memorised or added to reading queue
on 12-Jul-2017 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1434939952396
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Substitution effect and income effect
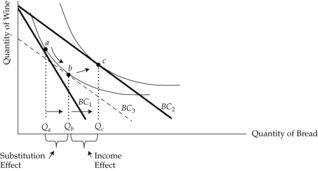
reduction. If the income reduction is just sufficient to leave him no better or morse than before the price change, we have removed the real income effect of the decrease in price. What’s left of his response must be due to the <span>substitution effect . So, we say that the substitution effect is shown by the move from point a to point b. If his income reduction were then restored, the resulting movement from point b to point
Flashcard 1451360390412
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
firm must cover variable cost before fixed cost. In the short run, if total revenue cannot cover total variable cost, the firm shuts down production to minimize loss, which would equal the amount of fixed cost. If total <span>variable cost exceeds total revenue in the long run, the firm will exit the market as a business entity to avoid the loss associated with fixed cost at zero production. By terminating busi
firm must cover variable cost before fixed cost. In the short run, if total revenue cannot cover total variable cost, the firm shuts down production to minimize loss, which would equal the amount of fixed cost. If total <span>variable cost exceeds total revenue in the long run, the firm will exit the market as a business entity to avoid the loss associated with fixed cost at zero production. By terminating busi
Flashcard 1622018231564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1623805005068
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1626081463564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 5. Uses and Analysis of the Balance Sheet
ing debt such as accounts payables, accrued expenses, and deferred taxes. This ratio is especially useful in analyzing a company with substantial financing from short-term borrowing. Total Debt Ratio = <span>Financial Leverage Ratio = Financial statement analysis aims to investigate a company's financial condition and operating performance. Using financial ratios helps to examine relationships among indi
ing debt such as accounts payables, accrued expenses, and deferred taxes. This ratio is especially useful in analyzing a company with substantial financing from short-term borrowing. Total Debt Ratio = <span>Financial Leverage Ratio = Financial statement analysis aims to investigate a company's financial condition and operating performance. Using financial ratios helps to examine relationships among indi
Flashcard 1626085395724
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1626110823692
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1626630917388
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 1. NPV and IRR
A company should choose those capital investment processes that maximize shareholder wealth. The net present value (NPV) of an investment is the present value of its cash inflows minus the present value of its cash outflows. The internal rate of return (IRR) is the discou
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 1. NPV and IRR
The internal rate of return (IRR) is the discount rate that makes net present value equal to 0. According to the NPV rule, a company should accept projects where the NPV is positive and reject those in which the NPV is negative. <span>A positive NPV suggests that cash inflows outweigh cash outflows on a present value basis. That is, the positive cash flows are sufficient to repay the initial investment along with the capital costs (opportunity cost) associated with the project. If the company must choose b
Flashcard 1626634849548
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 1. NPV and IRR
ater than the discount rate used (WACC) and reject those in which the IRR is less than the discount rate. An IRR greater than the WACC suggests that the project will more than repay the capital costs (opportunity costs) incurred. <span>There are three problems associated with IRR as a decision rule. Reinvestment The IRR is intended to provide a single number that represents the rate of return generated by a capital investment. As such, it is an easy number
Flashcard 1626637208844
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 1. NPV and IRR
le. Reinvestment The IRR is intended to provide a single number that represents the rate of return generated by a capital investment. As such, it is an easy number to interpret and understand. However, calculation of <span>the IRR assumes that all project cash flows can be reinvested to earn a rate of return exactly equal to the IRR itself. In other words, a project with an IRR of 6% assumes that all cash flows can be reinvested to earn exactly 6%. If the cash flows are invested at a rate lower than 6%, the realized return
Flashcard 1626639568140
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 1. NPV and IRR
y a capital investment. As such, it is an easy number to interpret and understand. However, calculation of the IRR assumes that all project cash flows can be reinvested to earn a rate of return exactly equal to the IRR itself. In other words, <span>a project with an IRR of 6% assumes that all cash flows can be reinvested to earn exactly 6%. If the cash flows are invested at a rate lower than 6%, the realized return will be less than the IRR. If the cash flows are invested at a rate higher than 6%, the realized return will
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 1. NPV and IRR
y a capital investment. As such, it is an easy number to interpret and understand. However, calculation of the IRR assumes that all project cash flows can be reinvested to earn a rate of return exactly equal to the IRR itself. In other words, <span>a project with an IRR of 6% assumes that all cash flows can be reinvested to earn exactly 6%. If the cash flows are invested at a rate lower than 6%, the realized return will be less than the IRR. If the cash flows are invested at a rate higher than 6%, the realized return will be greater than the IRR. Scale In most cases, NPV and IRR rules provide the same recommendation as to whether to accept or reject a given capital investment project. However, when
Flashcard 1626644286732
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 1. NPV and IRR
usive projects of greatly differing scale: one that requires a relatively small investment and returns relatively small cash flows, and another that requires a much larger investment and returns much larger cash flows. <span>Timing The other situation in which IRR is likely to contradict NPV is when there are two mutually-exclusive projects whose cash flows are timed very differently: one that receives its
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1626650053900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
When analyzing rates of return, our starting point is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula:
Flashcard 1626652413196
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
When analyzing rates of return, our starting point is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula:
Flashcard 1626654772492
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
When analyzing rates of return, our starting point is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula: P t = price per share at the end of time period t P (t-1) = price per share at the
Flashcard 1626657131788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
When analyzing rates of return, our starting point is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula: P t = price per share at the end of time period t P (t-1) = price per share at the end of time period t-1, the time period immediately
Flashcard 1626659491084
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
t is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula: <span>P t = price per share at the end of time period t P (t-1) = price per share at the end of time period t-1, the time period immediately preceding time period t P t - P t-1 = price appreciation of the investment D t = cash distributions received during time period t: for common stock, cash distribution is the dividend; for bonds, cash distribution is the coupon payment. It has two important characteristics: It has an element of time attached to it: monthly, quarterly or annual returns. HPR can be computed for any time period. It has n
Flashcard 1626663423244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
e end of time period t P (t-1) = price per share at the end of time period t-1, the time period immediately preceding time period t P t - P t-1 = price appreciation of the investment D t = cash distributions received during time period t: <span>for common stock, cash distribution is the dividend; for bonds, cash distribution is the coupon payment. It has two important characteristics: It has an element of time attached to it: monthly, quarterly or annual returns. HPR can be computed for any time period. It has n
Flashcard 1626666044684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
eceding time period t P t - P t-1 = price appreciation of the investment D t = cash distributions received during time period t: for common stock, cash distribution is the dividend; for bonds, cash distribution is the coupon payment. <span>It has two important characteristics: It has an element of time attached to it: monthly, quarterly or annual returns. HPR can be computed for any time period. It has no currency unit attached to it; the result holds regardless of the currency in which prices are denominated. Example A stock is currently worth $60. If you purchased the stock exactly one year ago for $50 and received a $2 dividend over the course of the year, what is your ho
Flashcard 1626668403980
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
period t is the capital gain (or loss) plus distributions divided by the beginning-of-period price (dividend yield). Note that for common stocks the distribution is the dividend; for bonds, the distribution is the coupon payment. <span>The holding period return for any asset can be calculated for any time period (day, week, month, or year) simply by changing the interpretation of the time interval. Return can be expressed in decimals (0.05), fractions (5/100), or as a percent (5%). These are all equivalent. &
Flashcard 1626670763276
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Holding Period Return
d). Note that for common stocks the distribution is the dividend; for bonds, the distribution is the coupon payment. The holding period return for any asset can be calculated for any time period (day, week, month, or year) simply <span>by changing the interpretation of the time interval. Return can be expressed in decimals (0.05), fractions (5/100), or as a percent (5%). These are all equivalent. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1631884021004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
The dollar-weighted rate of return is essentially the internal rate of return (IRR) on a portfolio. This approach considers the timing and amountof cash flows. It is affected by the timing of cash flows. If funds are added to a portfolio when the portfolio is performing well (poorly),
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
The dollar-weighted rate of return is essentially the internal rate of return (IRR) on a portfolio. This approach considers the timing and amountof cash flows. It is affected by the timing of cash flows. If funds are added to a portfolio when the portfolio is performing well (poorly), the dollar-weighted rate of return will be inflated (depressed). The time-weighted rate of return measures the compound growth rate of $1 initial investment over the measurement period. Time-weightedmeans that returns are averaged over t
Flashcard 1631928585484
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
rs the timing and amountof cash flows. It is affected by the timing of cash flows. If funds are added to a portfolio when the portfolio is performing well (poorly), the dollar-weighted rate of return will be inflated (depressed). <span>The time-weighted rate of return measures the compound growth rate of $1 initial investment over the measurement period. Time-weightedmeans that returns are averaged over time. This approach is not affected by the timing of cash flows; therefore, it is the preferred method of performance measurement. 
Flashcard 1631942741260
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
the portfolio is performing well (poorly), the dollar-weighted rate of return will be inflated (depressed). The time-weighted rate of return measures the compound growth rate of $1 initial investment over the measurement period. <span>Time-weightedmeans that returns are averaged over time. This approach is not affected by the timing of cash flows; therefore, it is the preferred method of performance measurement. Example Jayson bought a share of I
Flashcard 1631958732044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
eighted rate of return will be inflated (depressed). The time-weighted rate of return measures the compound growth rate of $1 initial investment over the measurement period. Time-weightedmeans that returns are averaged over time. <span>This approach is not affected by the timing of cash flows; therefore, it is the preferred method of performance measurement. Example Jayson bought a share of IBM stock for $100 on December 31, 2000. On December 31, 2001, he bought another share for $150. On December 31, 2002, he sold
Flashcard 1632002510092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
sub-period: HPR = (Dividends + Ending Price)/Beginning Price - 1. For the first year, HPR 1 : (150 + 10)/100 - 1 = 0.60. For the second year, HPR 2 : (280 + 20)/300 - 1 = 0. Calculate the time-weighted rate of return: <span>If the measurement period < 1 year, compound holding period returns to get an annualized rate of return for the year. If the measurement period > 1 year, take the geometric mean of the annual returns. <span><body><html>
Flashcard 1632046812428
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
For the second year, HPR 2 : (280 + 20)/300 - 1 = 0. Calculate the time-weighted rate of return: If the measurement period < 1 year, compound holding period returns to get an annualized rate of return for the year. <span>If the measurement period > 1 year, take the geometric mean of the annual returns. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1632708201740
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
Money market instruments are low-risk, highly liquid debt instruments with a maturity of one year or less. There are two types of money market instruments: interest-bearing instruments (e.g., bank certificates of deposit), and pure discount instruments (e.g., U.S. Treasury bills). Pure discount instruments such as T-bills are quoted differently than U.S. government bonds. They are quoted on a bank discount basis rather than on a price basis: &#
Flashcard 1632768494860
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
earing instruments (e.g., bank certificates of deposit), and pure discount instruments (e.g., U.S. Treasury bills). Pure discount instruments such as T-bills are quoted differently than U.S. government bonds. They are quoted on a <span>bank discount basis rather than on a price basis: r BD = the annualized yield on a bank discount basis D = the dollar discount, which is equal to the difference between the face v
Flashcard 1632800214284
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
bills). Pure discount instruments such as T-bills are quoted differently than U.S. government bonds. They are quoted on a bank discount basis rather than on a price basis: <span>r BD = the annualized yield on a bank discount basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on inves
Flashcard 1632835865868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
unt basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. <span>Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 =
Flashcard 1632864439564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
unt basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. <span>Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 =
Flashcard 1632883051788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
unt basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. <span>Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 =
Flashcard 1632905858316
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
tead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). <span>Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 = the initial price of the instrument P 1 = the price received for the instrument at its maturity D 1 = the cash distributio
Flashcard 1632930237708
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
gnores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: <span>P 0 = the initial price of the instrument P 1 = the price received for the instrument at its maturity D 1 = the cash distribution paid by the instrument at its maturity (that is, interest). Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, n
Flashcard 1633124486412
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
instrument at its maturity D 1 = the cash distribution paid by the instrument at its maturity (that is, interest). Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . <span>Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. &#
Flashcard 1633167740172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
ument at its maturity (that is, interest). Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, not face value. <span>It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest.
Flashcard 1633194216716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
#13; Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield. <span>The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of
Flashcard 1633214401804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
#13; Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield. <span>The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest.
Flashcard 1633232489740
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
se price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. <span>Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest. Example An investor buys a $1,000 face-value T-bill due
Flashcard 1633252412684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
se price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. <span>Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest. Example An investor buys a $1,000 face-value T-bill due in 60 days at a price of $990. Bank discount yield: (1000 - 990
Flashcard 1633271549196
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
se price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. <span>Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest. Example An investor buys a $1,000 face-value T-bill due in 60 days at a price of $990. Bank discount yield: (1000 - 990
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Zero-Coupon Bond
What is a 'Zero-Coupon Bond' <span>A zero-coupon bond, also known as an "accrual bond," is a debt security that doesn't pay interest (a coupon) but is traded at a deep discount, rendering profit at maturity when the bond is redeemed for its full face value. Some zero-coupon bonds are issued as such, while others are bonds that have been stripped of their coupons by a financial institution and then repackaged as zero-coupon bonds. Because t