Edited, memorised or added to reading queue
on 18-Aug-2018 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 149625149
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: <span>It is thus the ratio of the relative (percentage) change in the function's output \(f(a)\) with respect to the relative change in its input \(a\), for infinitesimal changes from a point . <span><body><html>
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Difference Of Squares | Brilliant Math & Science Wiki
ction contains examples and problems to boost understanding in the usage of the difference of squares identity: \(a^2-b^2=(a+b)(a-b)\). Here are the examples to learn the usage of the identity. <span>Rewrite \(5^2-2^2\) as a product. We have \[5^2-2^2 = (5-2) \times (5+2) = 3\times 7. \ _\square\] Calculate \(299\times 301\). You can brute force the answer to this problem by using a calculator, but we have a sweeter way. We can apply the difference of two squares identity. At fir
Flashcard 3199204461836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 3199210753292
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn Whipple’s disease, 87% are males, usually white and middle- aged. It presents with arthritis and arthralgia, progressing over years to weight loss and diarrhoea with abdominal pain, systemic symptoms of fever and weight loss. Peripheral lymphadenopat
Original toplevel document (pdf)
cannot see any pdfsFlashcard 3199212326156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn Whipple’s disease, 87% are males, usually white and middle- aged. It presents with arthritis and arthralgia, progressing over years to weight loss and diarrhoea with abdominal pain, systemic symptoms of fever and weight loss. Peripheral lymphadenopathy and involvement of the heart, lung, join
Original toplevel document (pdf)
cannot see any pdfsFlashcard 3199213899020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itarthritis and arthralgia, progressing over years to weight loss and diarrhoea with abdominal pain, systemic symptoms of fever and weight loss. Peripheral lymphadenopathy and involvement of the <span>heart, lung, joints and brain occur, simulating many neurological conditions <span>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 3199217044748
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 3199219404044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 3199224909068
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itin 10% of cases of IBD causing colitis a definitive diagnosis of either UC or CD is not possible and the diagnosis is termed colitis of undetermined type and etiology (CUTE).
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 3199228841228
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itJewish people are more prone to inflammatory bowel disease than any other ethnic group.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 3199230414092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 3199235132684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itCrohn's Disease and Ulcerative colitis are complex polygenic diseases and having a positive family history is the largest independent risk factor.
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Solving Identity Equations | Brilliant Math & Science Wiki
ave an account? Log in here. Quiz Solving Identity Equations Relevant For... Algebra > Polynomial Arithmetic Ram Mohith , Beakal Tiliksew , Mahindra Jain , and 1 other Jimin Khim contributed <span>An identity equation is an equation that is always true for any value substituted into the variable. \(_\square\) For example, \(2(x+1)=2x+2\) is an identity equation. One way of checking is by simplifying the equation. \[\begin{align} 2(x+1)&=2x+2\\ 2x+2&=2x+2\\ 2&=2. \end{align}\] \(2
Flashcard 3199243783436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Difference Of Squares | Brilliant Math & Science Wiki
ue View solutions What is Note: Try it without using a calculator. Correct! The answer is 1. 74% of people got this right. Continue View solutions Don't use a calculator! Further Extension Edit <span>Since the two factors are different by , the factors will always have the same parity. That is, if is even then must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: Problem Solving Edit The examples and problems in this sections are a bit hard
ue View solutions What is Note: Try it without using a calculator. Correct! The answer is 1. 74% of people got this right. Continue View solutions Don't use a calculator! Further Extension Edit <span>Since the two factors are different by , the factors will always have the same parity. That is, if is even then must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: Problem Solving Edit The examples and problems in this sections are a bit hard
Flashcard 3199247453452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Effective learning: Twenty rules of formulating knowledge | SuperMemo.com
not just learn once but you will repeat the material optimally (as in SuperMemo). The 20 rules of formulating knowledge in learning Do not learn if you do not understand Trying to learn things y<span>ou do not understand may seem like an utmost nonsense. Still, an amazing proportion of students commit the offence of learning without comprehension. Very often they have no other choice! The quality of many textbooks or lecture scripts is deplorable while examination deadlines are unmovable. If you are not a speaker of German, it is still possible to learn
not just learn once but you will repeat the material optimally (as in SuperMemo). The 20 rules of formulating knowledge in learning Do not learn if you do not understand Trying to learn things y<span>ou do not understand may seem like an utmost nonsense. Still, an amazing proportion of students commit the offence of learning without comprehension. Very often they have no other choice! The quality of many textbooks or lecture scripts is deplorable while examination deadlines are unmovable. If you are not a speaker of German, it is still possible to learn
Flashcard 3199249812748
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Effective learning: Twenty rules of formulating knowledge | SuperMemo.com
nce of learning without comprehension. Very often they have no other choice! The quality of many textbooks or lecture scripts is deplorable while examination deadlines are unmovable. If you are <span>not a speaker of German, it is still possible to learn a history textbook in German. The book can be crammed word for word. However, the time needed for such "blind learning" is astronomical. Even more important: The value of such knowledge is negligible. If you cram a German book on history, you will still know nothing of history. The German history
nce of learning without comprehension. Very often they have no other choice! The quality of many textbooks or lecture scripts is deplorable while examination deadlines are unmovable. If you are <span>not a speaker of German, it is still possible to learn a history textbook in German. The book can be crammed word for word. However, the time needed for such "blind learning" is astronomical. Even more important: The value of such knowledge is negligible. If you cram a German book on history, you will still know nothing of history. The German history
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Effective learning: Twenty rules of formulating knowledge | SuperMemo.com
learning" is astronomical. Even more important: The value of such knowledge is negligible. If you cram a German book on history, you will still know nothing of history. The German history book <span>example is an extreme. However, the materials you learn may often seem well structured and you may tend to blame yourself for lack of comprehension. Soon you may pollute your learning process with a great deal of useless material that treacherously makes you believe "it will be useful some day". Learn before you memorize Before you proceed with memorizing individual facts and rules, you need to build an overall picture of the learned knowledge. Only when individual pieces fit t
Flashcard 3199695457548
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itexample is an extreme. However, the materials you learn may often seem well structured and you may tend to blame yourself for lack of comprehension. Soon you may pollute your learning process with a great deal of useless material that treacherously makes you believe "it will be useful some day".
Original toplevel document
Effective learning: Twenty rules of formulating knowledge | SuperMemo.comlearning" is astronomical. Even more important: The value of such knowledge is negligible. If you cram a German book on history, you will still know nothing of history. The German history book <span>example is an extreme. However, the materials you learn may often seem well structured and you may tend to blame yourself for lack of comprehension. Soon you may pollute your learning process with a great deal of useless material that treacherously makes you believe "it will be useful some day". Learn before you memorize Before you proceed with memorizing individual facts and rules, you need to build an overall picture of the learned knowledge. Only when individual pieces fit t
Flashcard 3199899929868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
4 Steps to Reading a Textbook Quickly and Effectively
e lame. If you know Bruce Willis is dead, don’t watch the 6th Sense. But textbooks are rarely building to a suspenseful twist at the end. I promise. I’ve read a lot. They don’t come with surpris<span>e endings. “And then, Abraham Lincoln dodged the bullet!” Yep, that’s never going to be in a textbook. Want to try this strategy? Try reading your textbook chapter in this order: Go to the questions at th
e lame. If you know Bruce Willis is dead, don’t watch the 6th Sense. But textbooks are rarely building to a suspenseful twist at the end. I promise. I’ve read a lot. They don’t come with surpris<span>e endings. “And then, Abraham Lincoln dodged the bullet!” Yep, that’s never going to be in a textbook. Want to try this strategy? Try reading your textbook chapter in this order: Go to the questions at th
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 3203067940108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRewrite 52−22 as a product. We have 52−22=(5−2)×(5+2)=3×7. □
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikiction contains examples and problems to boost understanding in the usage of the difference of squares identity: \(a^2-b^2=(a+b)(a-b)\). Here are the examples to learn the usage of the identity. <span>Rewrite \(5^2-2^2\) as a product. We have \[5^2-2^2 = (5-2) \times (5+2) = 3\times 7. \ _\square\] Calculate \(299\times 301\). You can brute force the answer to this problem by using a calculator, but we have a sweeter way. We can apply the difference of two squares identity. At fir
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Difference Of Squares | Brilliant Math & Science Wiki
lor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209515896076
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by 2b , the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209517468940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by \(2b\), the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209519303948
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by \(2b\), the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 square
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209521138956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by \(2b\), the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the differ
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209522187532
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by \(2b\), the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares.
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
Flashcard 3209524022540
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRewrite 52−22 as a product. We have 52−22=(5−2)×(5+2)=3×7.
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikiction contains examples and problems to boost understanding in the usage of the difference of squares identity: \(a^2-b^2=(a+b)(a-b)\). Here are the examples to learn the usage of the identity. <span>Rewrite \(5^2-2^2\) as a product. We have \[5^2-2^2 = (5-2) \times (5+2) = 3\times 7. \ _\square\] Calculate \(299\times 301\). You can brute force the answer to this problem by using a calculator, but we have a sweeter way. We can apply the difference of two squares identity. At fir
Flashcard 3209525071116
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSince the two factors are different by \(2b\), the factors will always have the same parity. That is, if a−b is even then a+b must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not
Original toplevel document
Difference Of Squares | Brilliant Math & Science Wikilor{blue}{2014} \times \color{blue}{2014}\color{blue}{2014} - \color{blue}{2014}\color{red}{2013} \times \color{blue}{2014}\color{fuchsia}{2015} = ? \] Don't use a calculator! Further Extension <span>Since the two factors are different by \(2b\), the factors will always have the same parity. That is, if \(a-b\) is even then \(a+b\) must also be even, so the product is divisible by four. Or neither are divisible by 2, so the product is odd. This implies that numbers which are multiple of 2 but not 4 cannot be expressed as the difference of 2 squares. The product of two differences of two squares is itself a difference of two squares in two different ways: \[\begin{array} { l l l } \left(a^2-b^2\right)\left(c^2-d^2\right) &= (ac)
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
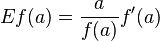
 .
.