Edited, memorised or added to reading queue
on 09-Jul-2014 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity of a function - Wikipedia, the free encyclopedia
er:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itIn mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using l
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itivatives meaning in words: It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using logarithms meaning in words: it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. <span><body><html>
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
Flashcard 149625138
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itad><head>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: It is thus the ratio of the relative (percentage) change in the function's output \(f(a)\) with respect to the relative change in its input \(a\), for infinitesimal chan
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
Flashcard 149625149
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] using functions and their derivatives meaning in words: <span>It is thus the ratio of the relative (percentage) change in the function's output \(f(a)\) with respect to the relative change in its input \(a\), for infinitesimal changes from a point . <span><body><html>
Original toplevel document
Elasticity of a function - Wikipedia, the free encyclopediaer:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
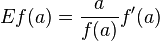
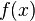 with respect to the relative change in its input
with respect to the relative change in its input 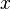 , for infinitesimal changes from a point
, for infinitesimal changes from a point 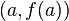 .
. 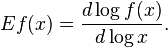
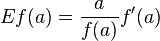
 .
.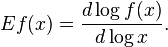
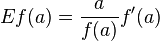
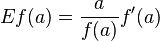
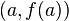 .
.