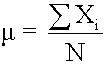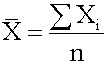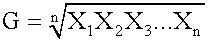Edited, memorised or added to reading queue
on 18-Jul-2017 (Tue)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1447328615692
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThere are four internal senses: The imagination , The sensuous memory , The common or central or synthesizing sense , and instinct .
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1635360050444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itrisk for contrast-induced nephropathy (CIN), and administration of intravenous isotonic saline (1-1.5 mL/kg/h) 3 to 12 hours before the procedure and continued for 6 to 24 hours afterward has been shown to decrease the incidence of CIN in high-risk patients.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1635361623308
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itrisk for contrast-induced nephropathy (CIN), and administration of intravenous isotonic saline (1-1.5 mL/kg/h) 3 to 12 hours before the procedure and continued for 6 to 24 hours afterward has been shown to decrease the incidence of CIN in high-risk patients.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1635363196172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itrisk for contrast-induced nephropathy (CIN), and administration of intravenous isotonic saline (1-1.5 mL/kg/h) 3 to 12 hours before the procedure and continued for 6 to 24 hours afterward has been shown to decrease the incidence of CIN in high-risk patients.
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1635366341900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRisk factors include age older than 75 years, diabetes mellitus, chronic kidney disease, conditions of decreased renal perfusion, and concurrent use of nephrotoxic drugs.
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1635370274060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itdiscontinuing omeprazole, repeat kidney function testing in 5 to 7 days is the most appropriate management for this patient with acute interstitial nephritis (AIN).
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1635373419788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itDrug-induced AIN is characterized by a slowly increasing serum creatinine 7 to 10 days after exposure; however, it can occur within 1 day of exposure if the patient has been exposed previously. Drug-induced AIN can also occur months after exposure, often with NSAI
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1635374992652
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itDrug-induced AIN is characterized by a slowly increasing serum creatinine 7 to 10 days after exposure; however, it can occur within 1 day of exposure if the patient has been exposed previously. Drug-induced AIN can also occur months after exposure, often with NSAIDs and proton pump inhibitors (PPIs)
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1635376565516
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ity>Drug-induced AIN is characterized by a slowly increasing serum creatinine 7 to 10 days after exposure; however, it can occur within 1 day of exposure if the patient has been exposed previously. Drug-induced AIN can also occur months after exposure, often with NSAIDs and proton pump inhibitors (PPIs)<body><html>
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1635379711244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAIN may be asymptomatic or present with mild, nonspecific symptoms; only 10% to 30% have the classic triad of fever, rash, and eosinophilia.
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1635398061324
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Measurement Scales
st level of measurement. It consists of assigning items to groups or categories. No quantitative information is conveyed and no ordering (ranking) of the items is implied. Nominal scales are qualitative rather than quantitative. <span>Religious preference, race, and sex are all examples of nominal scales. Another example is portfolio managers categorized as value or growth style will have a scale of 1 for value and 2 for growth. Frequency distributions are usually used to analyze data me
Flashcard 1636237184268
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
ency distribution. An interval, also called a class, is a set of values within which an observation falls. Each interval has a lower limit and an upper limit. Intervals must be all-inclusive and non-overlapping. <span>A frequency distribution is a tabular display of data categorized into a small number of non-overlapping intervals. Note that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This mean
Flashcard 1636239543564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
with individual numbers becomes laborious and messy. In such circumstances, it is neater and more convenient to summarize results into what is known as a frequency table. The data in the display is called a frequency distribution. <span>An interval, also called a class, is a set of values within which an observation falls. Each interval has a lower limit and an upper limit. Intervals must be all-inclusive and non-overlapping. A frequency distribution is a tabular display of data categor
Flashcard 1636241116428
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
with individual numbers becomes laborious and messy. In such circumstances, it is neater and more convenient to summarize results into what is known as a frequency table. The data in the display is called a frequency distribution. <span>An interval, also called a class, is a set of values within which an observation falls. Each interval has a lower limit and an upper limit. Intervals must be all-inclusive and non-overlapping. A frequency distribution is a tabular display of data categor
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
ency distribution. An interval, also called a class, is a set of values within which an observation falls. Each interval has a lower limit and an upper limit. Intervals must be all-inclusive and non-overlapping. <span>A frequency distribution is a tabular display of data categorized into a small number of non-overlapping intervals. Note that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too ma
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. <span>It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. <span>A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percentage of scores in each interval are displayed. This helps in the analysis of large amount of statistical data, and works with all types of measurement scales. Absolute frequency is the actual number of observations in a given interval. Relative frequency is the result of dividing the absolute frequency of e
Flashcard 1636249505036
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
of scores in each interval. The actual number of scores and the percentage of scores in each interval are displayed. This helps in the analysis of large amount of statistical data, and works with all types of measurement scales. <span>Absolute frequency is the actual number of observations in a given interval. Relative frequency is the result of dividing the absolute frequency of each return interval by the total number of observations. Cumulative absol
Flashcard 1636251864332
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
al are displayed. This helps in the analysis of large amount of statistical data, and works with all types of measurement scales. Absolute frequency is the actual number of observations in a given interval. <span>Relative frequency is the result of dividing the absolute frequency of each return interval by the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the l
Flashcard 1636254223628
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
olute frequency is the actual number of observations in a given interval. Relative frequency is the result of dividing the absolute frequency of each return interval by the total number of observations. <span>Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
by the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. <span>The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as
Flashcard 1636258155788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
t be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. <span>Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares compris
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
mber of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. <span>Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 3. Frequency Distributions
ed into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. <span>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distributi
Flashcard 1636263660812
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
values (i.e., all values can be included in the data set). Examples would include the height of a person and the time to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. <span>There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distribution. It is constructed as follows: The class frequencies are shown on the vertical (y) axis (by
Flashcard 1636296166668
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Different Yield Measures of a U.S. Treasury Bill
unt basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. <span>Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 =
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1636462628108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
mber of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. <span>Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. Continuous: The values in the data set can be measu
Flashcard 1636464987404
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
ed into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as the number of children in a family or the number of shares comprising an index. <span>Continuous: The values in the data set can be measured. There are normally lots of decimal places involved and (theoretically, at least) there are no gaps between permissible values (i.e., all values can be included in the data set). Example
Flashcard 1636467346700
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
me to complete an assignment. These values can be measured using sufficiently accurate tools to numerous decimal places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. <span>A histogram is a bar chart that displays a frequency distribution. It is constructed as follows: The class frequencies are shown on the vertical (y) axis (by the heights of bars drawn next to each other). The classes (intervals) are shown
Flashcard 1636469705996
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
al places. There are two methods that graphically represent continuous data: histograms and frequency polygons. 1. A histogram is a bar chart that displays a frequency distribution. It is constructed as follows: <span>The class frequencies are shown on the vertical (y) axis (by the heights of bars drawn next to each other). The classes (intervals) are shown on the horizontal (x) axis. There is no space between the bars. From a histogram, we can see quickly where most of the observa
Flashcard 1636472065292
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
polygons. 1. A histogram is a bar chart that displays a frequency distribution. It is constructed as follows: The class frequencies are shown on the vertical (y) axis (by the heights of bars drawn next to each other). <span>The classes (intervals) are shown on the horizontal (x) axis. There is no space between the bars. From a histogram, we can see quickly where most of the observations lie. The shapes of histograms will vary, depending on th
Flashcard 1636474424588
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
ays a frequency distribution. It is constructed as follows: The class frequencies are shown on the vertical (y) axis (by the heights of bars drawn next to each other). The classes (intervals) are shown on the horizontal (x) axis. <span>There is no space between the bars. From a histogram, we can see quickly where most of the observations lie. The shapes of histograms will vary, depending on the choice of the size of the interva
Flashcard 1636476783884
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
#13; The class frequencies are shown on the vertical (y) axis (by the heights of bars drawn next to each other). The classes (intervals) are shown on the horizontal (x) axis. There is no space between the bars. <span>From a histogram, we can see quickly where most of the observations lie. The shapes of histograms will vary, depending on the choice of the size of the intervals. 2. The frequency polygon is another means of graphically displaying data. It is si
Flashcard 1636479143180
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
the heights of bars drawn next to each other). The classes (intervals) are shown on the horizontal (x) axis. There is no space between the bars. From a histogram, we can see quickly where most of the observations lie. <span>The shapes of histograms will vary, depending on the choice of the size of the intervals. 2. The frequency polygon is another means of graphically displaying data. It is similar to a histogram but the bars are replaced by a line joined together. It is constructe
Flashcard 1636481502476
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
s. There is no space between the bars. From a histogram, we can see quickly where most of the observations lie. The shapes of histograms will vary, depending on the choice of the size of the intervals. 2. <span>The frequency polygon is another means of graphically displaying data. It is similar to a histogram but the bars are replaced by a line joined together. It is constructed in the following manner: Absolute frequency for each interval is plotted
Flashcard 1636484648204
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
f graphically displaying data. It is similar to a histogram but the bars are replaced by a line joined together. It is constructed in the following manner: Absolute frequency for each interval is plotted on the vertical (y) axis. <span>The midpoint of each class (interval) is shown on the horizontal (x) axis. Neighboring points are connected with a straight line. Unlike a histogram, a frequency polygon adds a degree of continuity to the presentation of the distribution. It
Flashcard 1636487007500
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
e following manner: Absolute frequency for each interval is plotted on the vertical (y) axis. The midpoint of each class (interval) is shown on the horizontal (x) axis. Neighboring points are connected with a straight line. <span>Unlike a histogram, a frequency polygon adds a degree of continuity to the presentation of the distribution. It is helpful, when drawing a frequency polygon, first to draw a histogram in pencil, then to plot the points and join the lines, and finally to rub out the histogram. In th
Flashcard 1636489366796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
first to draw a histogram in pencil, then to plot the points and join the lines, and finally to rub out the histogram. In this way, the histogram can be used as an initial guide to drawing the polygon. <span>The relative frequency for a class is calculated by dividing the number of observations in a class by the total number of observations and converting this figure to a percentage (multiplying the fraction by 100). Simply, relative frequency is the percentage of total observations falling within each interval. It is another way of analyzing data; it tells us, for each class, what proportion (or pe
Flashcard 1636491726092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
; The relative frequency for a class is calculated by dividing the number of observations in a class by the total number of observations and converting this figure to a percentage (multiplying the fraction by 100). <span>Simply, relative frequency is the percentage of total observations falling within each interval. It is another way of analyzing data; it tells us, for each class, what proportion (or percentage) of data falls in that class. Let's look at an example. The fo
Flashcard 1636494085388
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Frequency Distributions
st one is -27%. Let's use 6 non-overlapping intervals, each with a width of 10%. The first interval starts at -27% and the last one ends at 33%. Therefore, the entire range of the HPRs is covered. Hint: <span>If, in an examination, your relative frequency column does not sum to 1 (or 100%), you know that you have made a mistake. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1636515319052
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
Measures of central tendency specify where data are centered. They attempt to use a typical value to represent all the observations in the data set. Population Mean The population mean is the average for a finite populatio
Flashcard 1636517678348
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
head><head> Measures of central tendency specify where data are centered. They attempt to use a typical value to represent all the observations in the data set. Population Mean The population mean is the average for a finite population. It is unique; a given population has only one mean. where: N = the number of observations in the entire population X i = the ith observation ΣX i = add up X i , where i is from 0 to
Flashcard 1636520037644
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
represent all the observations in the data set. Population Mean The population mean is the average for a finite population. It is unique; a given population has only one mean. <span>where: N = the number of observations in the entire population X i = the ith observation ΣX i = add up X i , where i is from 0 to N Sample Mean The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean.
Flashcard 1636522396940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
que; a given population has only one mean. where: N = the number of observations in the entire population X i = the ith observation ΣX i = add up X i , where i is from 0 to N <span>Sample Mean The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample Arithmetic Mean The arithmetic mean is what is commonly called the a
Flashcard 1636524756236
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
stic and is used to estimate the population mean. where n = the number of observations in the sample Arithmetic Mean The arithmetic mean is what is commonly called the average. <span>The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the
Flashcard 1636527115532
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
here n = the number of observations in the sample Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. <span>If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency.
Flashcard 1636529474828
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
thmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. <span>If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The
Flashcard 1636531834124
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
an. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. <span>This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is us
Flashcard 1636534193420
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
ulation, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. <span>When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods
Flashcard 1636536552716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
e assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. <span>All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is t
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
r of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. <span>All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each valu
Flashcard 1636540484876
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
(return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. <span>A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distanc
Flashcard 1636542844172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
d ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. <span>The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: Th
Flashcard 1636545203468
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
thmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. <span>Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determi
Flashcard 1636547562764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
etic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. <span>The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important
Flashcard 1636549922060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
etic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. <span>The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater th
Flashcard 1636552281356
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
13; The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In othe
Flashcard 1636554902796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
s: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean <span>The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by perio
Flashcard 1636557262092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
f the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. <span>It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispe
Flashcard 1636559621388
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. <span>When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean.
Flashcard 1636561980684
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
; It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. <span>The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed v
Flashcard 1636564602124
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
r measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. <span>This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight
Flashcard 1636566961420
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean <span>The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to each value. Notice that the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The
Flashcard 1636569320716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
alues as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to each value. Notice that <span>the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The assets are weighted on their market values relative to the market value of the portfolio. When we take a weighted average of forward-looking data, the weighted mean is called expect
Flashcard 1636571942156
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
assigns equal weight to each value. Notice that the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The assets are weighted on their market values relative to the market value of the portfolio. <span>When we take a weighted average of forward-looking data, the weighted mean is called expected value. Example A year ago, a certain share had a price of $6. Six months ago, the same share had a price of $6.20. The share is now trading at $7.50. Because the most
Flashcard 1636574301452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
ice inflates the weighted mean relative to the un-weighted mean. Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. <span>The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation.
Flashcard 1636576660748
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. <span>To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observation
Flashcard 1636579020044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and <span>find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single mid