Edited, memorised or added to reading queue
on 05-May-2018 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 2287313227020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open it1.2 Le plan Définition 2 : Un plan P peut être défini par trois points A, B, C non alignés. Il est alors noté (ABC). Un plan peut être aussi défini par deux droites sécantes ou strictement parallèles.
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 2287319518476
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
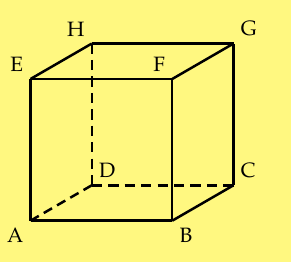
Open it1.3.1 Relations entre deux droites Propriété 1 : Deux droites, dans l’espace, peuvent être : • coplanaires, si ces deux droites appartiennent à un même plan [(AF) et (BE)] ; • secantes, si ces deux droites se coupent en un point [(AB) et (AD)] ; • parallèles, si ces deux droites sont coplanaires et n’ont aucun point commun ou si ces deux droites sont confondues [(AB) et (HG)] ; • non coplanaires [(AB) et (DG)]. A B C D E F G H Conclusion : Deux droites peuvent être parallèles, sécantes ou non coplanaires.
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 2328764747020
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
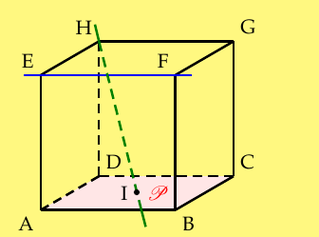
Open it1.3.2 Relations entre une droite et un plan Propriété 2 : Une droite et un plan peuvent être : • parallèles : si la droite et le plan n’ont aucun point commun ou si la droite est contenue dans le plan [(EF) et P ] ; • sécantes : si la droite et le plan ont un seul point commun [(HI) et P]
Original toplevel document (pdf)
cannot see any pdfsFlashcard 2328766844172
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open it1.3.2 Relations entre une droite et un plan Propriété 2 : Une droite et un plan peuvent être : • parallèles : si la droite et le plan n’ont aucun point commun ou si la droite est contenue dans le plan [(EF) et P ] ; • sécantes : si la droite et le plan ont un seul point commun [(HI) et P]
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 2332379974924
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
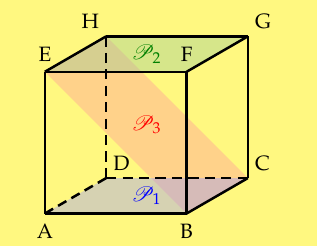
Open it1.3.3 Relation entre deux plans Propriété 3 : Deux plans peuvent être : • parallèles : si les deux plans n’ont au- cun points commun ou si les deux plans sont confondus (P 1 ∩P 2 = ∅) • sécants : si les deux plans ont une droite en commun. (P 1 ∩ P 3 = (BC))
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 2337519308044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
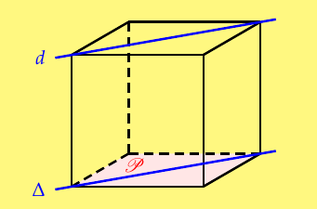
Open it1.4.1 Parallélisme d’une droite et d’un plan Théorème 1 : Si une droite d est parallèle à une droite ∆ contenue dans un plan P, alors d est parallèle à P. d // ∆ ∆ ⊂ P ) ⇒ d // P
Original toplevel document (pdf)
cannot see any pdfs| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |










 ...
...