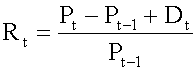BuboFlash - helps with learning

Edited, memorised or added to reading queue

Do you want BuboFlash to help you learning these things? Click here to log in or create user.

Flashcard 1430814854412

Tags

#cfa #cfa-level-1 #economics #microeconomics #reading-14-demand-and-supply-analysis-consumer-demand #section-3-utility-theory #study-session-4

Question

We assume that when comparing any three distinct bundles, A, B, and C, if A is preferred to B, and simultaneously B is preferred to C, then it must be true that A is preferred to C. This assumption is referred to as the assumption of [...] , and it is assumed to hold for indifference as well as for strict preference.

Answer

transitive preferences

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
an>We assume that when comparing any three distinct bundles, A, B, and C, if A is preferred to B, and simultaneously B is preferred to C, then it must be true that A is preferred to C. This assumption is referred to as the assumption of transitive preferences , and it is assumed to hold for indifference as well as for strict preference.<body><html>

Original toplevel document

3. UTILITY THEORY: MODELING PREFERENCES AND TASTES
that about his two children. In effect, the father neither prefers one to the other nor is, in any meaningful sense, indifferent between the two. The assumption of complete preferences cannot accommodate such a response. Second, we assume that when comparing any three distinct bundles, A, B, and C, if A is preferred to B, and simultaneously B is preferred to C, then it must be true that A is preferred to C. This assumption is referred to as the assumption of transitive preferences , and it is assumed to hold for indifference as well as for strict preference. This is a somewhat stronger assumption because it is essentially an assumption of rationality. We would say that if a consumer prefers a skiing holiday to a diving holiday and a diving

Flashcard 1435741064460

Tags

#2-1-3-economic-rent #2-1-types-of-profit-measures #cfa-level-1 #economics #has-images #microeconomics #reading-15-demand-and-supply-analysis-the-firm #section-2-objectives-of-the-firm #study-session-4

Question

The amount of this economic rent is calculated as _[...].

Answer

(P₂ – P₁) × Q₁

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

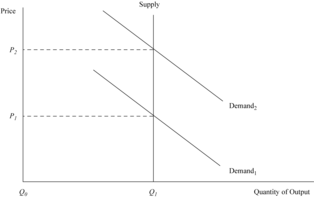
Economic rent
to the business that supplies the item. When demand increases from Demand 1 to Demand 2 , price rises to P 2 , where at this higher price level economic rent is created. The amount of this economic rent is calculated as (P 2 – P 1 ) × Q 1 . The firm has not done anything internally to merit this special reward: It benefits from an increase in demand in conjunction with a supply curve that does not fully adjust with an in

Flashcard 1442637548812

Tags

#cfa-level-1 #microeconomics #monopoly #reading-16-the-firm-and-market-structures #section-2-analysis-of-mkt-structures #study-session-4

Question

In most cases, the monopoly power provider is allowed to earn a normal return on its investment and prices are set by [...] to allow that return.

Answer

the regulatory authority

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
The most common example of a regulated monopoly is the local electrical power provider. In most cases, the monopoly power provider is allowed to earn a normal return on its investment and prices are set by the regulatory authority to allow that return.

Original toplevel document

2. ANALYSIS OF MARKET STRUCTURES
one of the carriers changes its pricing package, others will likely retaliate. Understanding the market structure of oligopoly markets can help in identifying a logical pattern of strategic price changes for the competing firms. Finally, the least competitive market structure is monopoly . In pure monopoly markets, there are no other good substitutes for the given product or service. There is a single seller, which, if allowed to operate without constraint, exercises considerable power over pricing and output decisions. In most market-based economies around the globe, pure monopolies are regulated by a governmental authority. The most common example of a regulated monopoly is the local electrical power provider. In most cases, the monopoly power provider is allowed to earn a normal return on its investment and prices are set by the regulatory authority to allow that return. 2.2. Factors That Determine Market Structure Five factors determine market structure: The number and relative size of firms

Flashcard 1449953725708

Tags

#cfa-level-1 #fra-introduction #reading-22-financial-statement-analysis-intro #study-session-7

Question

In evaluating financial reports, analysts typically have a specific economic decision in mind.

Examples of these decisions include the following:

Evaluating a subsidiary or operating division of [...]
Deciding whether to make a [...] or other private equity investment.

Answer

a parent company.

venture capital

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
merger or acquisition candidate. Evaluating a subsidiary or operating division of a parent company. Deciding whether to make a venture capital or other private equity investment. Determining the creditworthiness of a company in order to decide whether to extend a loan to the company and if so, what terms to offer. <body><html>

Original toplevel document

2. SCOPE OF FINANCIAL STATEMENT ANALYSIS
ing, and financing decisions but do not necessarily rely on analysis of related financial statements. They have access to additional financial information that can be reported in whatever format is most useful to their decision.) In evaluating financial reports, analysts typically have a specific economic decision in mind. Examples of these decisions include the following: Evaluating an equity investment for inclusion in a portfolio. Evaluating a merger or acquisition candidate. Evaluating a subsidiary or operating division of a parent company. Deciding whether to make a venture capital or other private equity investment. Determining the creditworthiness of a company in order to decide whether to extend a loan to the company and if so, what terms to offer. Extending credit to a customer. Examining compliance with debt covenants or other contractual arrangements. Assigning a debt rating to a company or bond issue. Valuing a security for making an investment recommendation to others. Forecasting future net income and cash flow. These decisions demonstrate certain themes in financial analysis. In general, analysts seek to examine the past and current performance and financial position of a

Flashcard 1533057568012

Tags

#cfa #cfa-level-1 #economics #reading-15-demand-and-supply-analysis-the-firm #section-3-analysis-of-revenue-costs-and-profit

Question

If a firm can cover its variable costs but not all of the total costs, the firm should attempt to operate by [...] to buy time to return operations back to profitability.

Answer

negotiating special arrangements with creditors

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Shutdown Analysis
For the most recent financial reporting period, a business domiciled in Ecuador (which recognizes the US dollar as an official currency) has revenue of $2 million and total costs of $2.5 million, which are or can be broken down into total fixed cost of $1 million and total variable cost of $1.5 million. The net loss on the firm’s income statement is reported as $500,000 (ignoring tax implications). In prior periods, the firm had reported profits on its operations. What decision should the firm make regarding operations over the short term? What decision should the firm make regarding operations over the long term? Assume the same business scenario except that revenue is now $1.3 million, wh

Flashcard 1621029686540

Tags

#cashflow-statement

Question

CFO does not include cash outlays for [...]

Answer

replacing old equipment

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Cash Flow Statement Analysis
s point of view, cash flows from operation activities have two major drawbacks: CFO does not include charges for the use of long-lived assets. Recall that depreciation is added back to net income in arriving at CFO. CFO does not include cash outlays for replacing old equipment. Free Cash Flow (FCF) is intended to measure the cash available to a company for discretionary uses after making all required cash outlays. It accoun

Flashcard 1621047512332

Tags

#cashflow-statement

Question

FCFF = NI + NCC + Int (1 - Tax rate) - FCInv - WCInv

NI= [...]

NCC= [...]

Answer

NI: Net income available to common shareholders.
NCC: Net non-cash charges.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Cash Flow Statement Analysis
; Free cash flow = CFO - capital expenditure Free Cash Flow to the Firm (FCFF): Cash available to shareholders and bondholders after taxes, capital investment, and WC investment. FCFF = NI + NCC + Int (1 - Tax rate) - FCInv - WCInv NI: Net income available to common shareholders. It is the company's earnings after interest, taxes and preferred dividends. NCC: Net non-cash

Flashcard 1621240712460

Question

The indirect method adjusts net income for all non-cash items and the net changes in [...].

Answer

the operating working capital accounts

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 2. Preparing the Cash Flow Statement
; It adjusts each item in the income statement to its cash equivalent. It shows operating cash receipts and payments. More cash flow information can be obtained and it is more easily understood by the average reader. The indirect method reconciles net income to net cash flow from operating activities by adjusting net income for all non-cash items and the net changes in the operating working capital accounts. It shows why net income and operating cash flows differ. It is used by most companies. The direct and indirect methods are alternative formats for reporti

Flashcard 1622016396556

Tags

#tvm

Question

One can always find the future value of a series of unequal cash flows by [...]

Answer

compounding the cash flows one at a time.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1626659491084

Tags

#has-images #reading-7-discounted-cashflows-applications

Question

P_t = [...]
P_(t-1) = price per share at the end of time period t-1, the time period immediately preceding time period t
P_t - P_t-1 = [...]
D_t = [...]

Answer

price per share at the end of time period t

price appreciation of the investment

cash distributions received during time period t

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 2. Holding Period Return
t is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula: P t = price per share at the end of time period t P (t-1) = price per share at the end of time period t-1, the time period immediately preceding time period t P t - P t-1 = price appreciation of the investment D t = cash distributions received during time period t: for common stock, cash distribution is the dividend; for bonds, cash distribution is the coupon payment. It has two important characteristics: It has an element of time attached to it: monthly, quarterly or annual returns. HPR can be computed for any time period. It has n

Flashcard 1635395702028

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] scales are qualitative rather than quantitative.

Answer

Nominal scales

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 2. Measurement Scales
3; Nominal Scale Nominal measurement represents the weakest level of measurement. It consists of assigning items to groups or categories. No quantitative information is conveyed and no ordering (ranking) of the items is implied. Nominal scales are qualitative rather than quantitative. Religious preference, race, and sex are all examples of nominal scales. Another example is portfolio managers categorized as value or growth style will have a scale of 1 f

Flashcard 1636536552716

Tags

#reading-8-statistical-concepts-and-market-returns

Question

All [...] and [...] (measurement scales) data sets have an arithmetic mean.

Answer

interval

ratio

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Measures of Center Tendency
e assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is t

Flashcard 1636549922060

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The arithmetic mean has the following disadvantages:

The mean cannot be determined for [...]

Answer

an open-ended data set (i.e., n is unknown).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Measures of Center Tendency
etic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater th

Flashcard 1636824386828

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In a frequency distribution if too many intervals are used, [...]

Answer

we may not summarize enough.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
In a frequency distribution It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough.

Original toplevel document

Subject 3. Frequency Distributions
that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent

Flashcard 1636826221836

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The following steps are required when organizing data into a frequency distribution.

Identify [...].
Setup classes (groups into which data is divided).
Add up the number of observations and assign each observation to its class.
Count the number of observations in each class.

Answer

the highest and lowest values of the observations

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign

Original toplevel document

Subject 3. Frequency Distributions
by the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as

Flashcard 1636832251148

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The following steps are required when organizing data into a frequency distribution.

Identify the highest and lowest values of the observations
Setup classes (groups into which data is divided).
Add up the number of observations and assign each observation to its class.
[...]

Answer

Count the number of observations in each class.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Original toplevel document

Flashcard 1636861611276

Tags

#reading-9-probability-concepts

Question

[...] is a quantity whose future outcomes are uncertain.

Answer

random variable

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636867902732

Tags

#reading-9-probability-concepts

Question

To save words, it is common to use [...] to represent a defined event.

Answer

a capital letter in italics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636871834892

Tags

#reading-9-probability-concepts

Question

The two defining properties of a probability are as follows:

The probability of any event E is [...]
The sum of the probabilities of any set of mutually exclusive and exhaustive events equals 1.

Answer

a number between 0 and 1: 0 ≤ P(E) ≤ 1.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636873669900

Tags

#reading-9-probability-concepts

Question

The two defining properties of a probability are as follows:

The probability of any event E is a number between 0 and 1: 0 ≤ P(E) ≤ 1.
The [...]

Answer

sum of the probabilities of any set of mutually exclusive and exhaustive events equals 1.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636875504908

Tags

#reading-9-probability-concepts

Question

Covering or containing all possible outcomes.

Answer

Exhaustive

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636877339916

Tags

#reading-9-probability-concepts

Question

P followed by parentheses stands for [...]

Answer

the probability of (the event in parentheses)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637079452940

Tags

#reading-9-probability-concepts

Question

In investments, we often estimate the probability of an event as a [...]

Answer

relative frequency of occurrence based on historical data.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637146299660

Tags

#reading-9-probability-concepts

Question

Relationships must be stable through time for [...] to be accurate.

Answer

Empirical probabilities

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637149969676

Tags

#reading-9-probability-concepts

Question

Can we calculate a reliable empirical probability for a very rare event?

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637151804684

Tags

#reading-9-probability-concepts

Question

A probability drawing on personal judgment is called a [...]

Answer

Subjective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637155736844

Tags

#reading-9-probability-concepts

Question

There are cases in which we have no empirical probability to use at all, then we would be making a [...]

Answer

Subjective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637208427788

Tags

#reading-9-probability-concepts

Question

The probability in answer to the straightforward question “What is the probability of this event A?” is an [...]

Answer

unconditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637262429452

Tags

#reading-9-probability-concepts

Question

To state an exact definition of conditional probability, we first need to introduce the concept of [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637264264460

Tags

#reading-9-probability-concepts

Question

“What is the probability of both A and B happening?” The answer to this question is a [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637267934476

Tags

#reading-9-probability-concepts

Question

the joint probability of A and B is the [...] .

Answer

sum of the probabilities of the outcomes they have in common

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637556555020

Tags

#reading-9-probability-concepts

Question

Given odds for E of “a to b,” the implied probability of E is [...]

Answer

a/(a + b).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Odds
ated in terms of odds as follows: Probability Stated as Odds. Given a probability P(E), Odds for E = P(E)/[1 − P(E)]. The odds for E are the probability of E divided by 1 minus the probability of E. Given odds for E of “a to b,” the implied probability of E is a/(a + b). In the example, the statement that the odds for the company’s EPS for FY2014 beating $0.69 are 1 to 7 means that the speaker believes the probability of th

Flashcard 1637558914316

Tags

#reading-9-probability-concepts

Question

Given odds against E of “a to b,” the implied probability of [...]

Answer

E is b/(a + b).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Odds
y’s EPS for FY2014 beating $0.69 are 1 to 7 means that the speaker believes the probability of the event is 1/(1 + 7) = 1/8 = 0.125. Odds against E = [1 − P(E)]/P(E), the reciprocal of odds for E. Given odds against E of “a to b,” the implied probability of E is b/(a + b). The statement that the odds against the company’s EPS for FY2014 beating $0.69 are 15 to 1 is consistent with a belief that the probability of the event is

Flashcard 1641023147276

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Cual es el acrónimo para la construccion de una frequecy table?

Answer

SCIWAC

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641029700876

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Construction of a frequency distribution

3.- I [...]

4.-W [...]

Answer

Intervals creation

Width determination

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Frequency distribution steps
Construction of a Frequency Distribution. Sort (in ascending order) Calculate the range (Range = Maximum value − Minimum value) Intervals creation (decide the number you will put in the frequency distribution, k.) Width determination ( interval width = Range/k.) Add the interval width to the minimum value (stop after reaching an interval that includes the maximum value) Count (the number of observations in each i

Flashcard 1641032060172

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Construction of a frequency distribution

3.- Intervals creation ( [...] .)

4.-Width determination (interval width [...] )

Answer

decide the number you will put in the frequency distribution, k

interval width = Range/k.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641034681612

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Construction of a Frequency Distribution.

5.-A [...]

6.-C [...]

Answer

Add the interval width to the minimum value

Count the number of observations in each interval

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Frequency distribution steps
alculate the range (Range = Maximum value − Minimum value) Intervals creation (decide the number you will put in the frequency distribution, k.) Width determination ( interval width = Range/k.) Add the interval width to the minimum value (stop after reaching an interval that includes the maximum value) Count (the number of observations in each interval) Table (make a table of intervals from small to large that shows the number of observations in each one) <body><html>

Flashcard 1641037040908

Tags

#reading-8-statistical-concepts-and-market-returns

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Frequency distribution steps
ion ( interval width = Range/k.) Add the interval width to the minimum value (stop after reaching an interval that includes the maximum value) Count (the number of observations in each interval) Table (make a table of intervals from small to large that shows the number of observations in each one) <body><html>

Flashcard 1641047002380

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Starting from small K to larger, what give you the cue there are too many?

Answer

if a lot of the intervals are mostly empty

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641060633868

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A property and potential drawback of the arithmetic mean is its [...]

Answer

sensitivity to extreme values

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641079508236

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The [...] is the only measure of central tendency that can be used with nominal data

Answer

mode

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641107033356

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In investments, what do we use to average a time series of rates of return on an asset or a portfolio?

Answer

we use the geometric

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641171520780

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When in a histograms there are only midpoints showing how do you find out the interval width?

Answer

substract any Midpoint - Midpoint_-1and you have the interval width.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641204550924

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Linear interpolation for a value of 12.75 for Py

Py ≈ [...]

Answer

X₁₂ + (12.75 − 12) (X₁₃ − X₁₂).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641208220940

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The nearest whole numbers below and above L_y establish the positions of observations that bracket P_y and then [...] of those two observations.

Answer

interpolate between the values

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644336909580

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The difference between the third and first quartiles of a dataset.

Answer

Interquatile range

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644363910412

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The expected value of squared deviations from a random variable’s expected value.

Answer

Variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644395891980

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The sample standard deviation is [...]

Answer

The positive square root of the sample variance.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644397726988

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The mean absolute deviation will always be less than or equal to the standard deviation because [...]

Answer

standard deviation gives more weight to large deviations than to small ones

(remember, the deviations are squared).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644545838348

Tags

#reading-8-statistical-concepts-and-market-returns

Question

One important characteristic of interest to analysts is the degree of [...] in return distributions.

Answer

symmetry

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644583324940

Tags

#reading-8-statistical-concepts-and-market-returns

Question

As a reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of [...] would be considered unusually large.

Answer

±0.5

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Open it
Note that as n becomes large, the expression reduces to the mean cubed deviation, SK ≈ (1/n) n∑ i=1 (Xi−X) 3 / s 3 . As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.

Flashcard 1644705484044

Tags

#reading-7-discounted-cashflows-applications

Question

If we know r_MM, then:

EAY = (1 + r_MM x t/360) [...]

Answer

EAY = (1 + r_MM x t/360)^365/t - 1

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
ld: (360 x 6%)/(360 - 60 x 6%) = 6.0606% If we know HPY, then: EAY = (1 + HPY) 365/t - 1 r MM = HPY x 360/t If we know EAY, then: HPY = ( 1 + EAY) t/365 - 1 r MM = [(1 + EAY) t/365 - 1] x (360/t) If we know r MM , then: HPY = r MM x (t/360) EAY = (1 + r MM x t/360) 365/t - 1 <body><html>

Flashcard 1644733795596

Tags

#reading-8-statistical-concepts-and-market-returns

Question

What would you use to compute the growth rate of a financial variable such as earnings or sales, given a set of info?

Answer

The geometric mean return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644744281356

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When in a histograms there are only midpoints showing how do you find out the interval classes?

Assume you have the interval width

Answer

You can get the classes by adding 1/2 of the interval width to both sides of the Midpoint.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644757912844

An Arab of the tribe of Tamim called Hammam b. Ghalib (al-Farazdaq) visited a clan not his own, the Banii Minqar, also belonging to Tamim. A woman, waking up her daughter called Zamya, found a snake in her clothes. She cried for help and Hammam chased the snake away. Hammam was attracted to the girl: he touched and kissed her, but she resisted and he left, making a mocking epigram on her and her clan. When her relatives heard this, they were angry and one of them called Amr (or Imran) b. Murra, was sent to play a trick upon Hammam' s sister, Jithin. Amr lay in wait for her and approached her unawares when, at night, she left her tent 'to do her business'. He put his hands on her hip and her leg and dragged her along for some distance. She cried out and when her tribesmen hastened to the scene Amr fled. In another version, there were, in fact, three other men, who together with Amr/lmran dragged Jithin from her tent.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 1644760272140

That was all; no more physical recriminations took place, nobody was raped or killed. We would not have known about the affair if this Hammam, Jicthin's brother, had not been a famous poet better known as al-Farazdaq, one of the great poets of the Umayyad period, and if he had not been involved in a protracted poetic battle, a 'flyting' or scolding match exchanging verbal abuse, with another giant of Arabic literary history, the poet Jarir b. c Atiyya. Jarir, universally lauded as a poet excelling in delicate love lyrics, heard about the matter and exploited it repeatedly in many of his lampooning poems, called naqirit;l,,2 grossly blowing up the incident by graphically depicting a gang rape in obscene detail, while accusing the victim's brother of being scandalously remiss in rescuing her.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 1644761845004

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Flashcard 1644775476492

Tags

#reading-8-statistical-concepts-and-market-returns

Question

If not equal, which is always less MAD or standard deviation?

Answer

Mean Absolute Deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644781505804

#reading-8-statistical-concepts-and-market-returns #skewness

The normal distribution has the following characteristics:

Its mean and median are equal.
It is completely described by two parameters—its mean and variance.
Roughly 68 percent of its observations lie between plus and minus one standard deviation from the mean; 95 percent lie between plus and minus two standard deviations; and 99 percent lie between plus and minus three standard deviations.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644783865100

#reading-8-statistical-concepts-and-market-returns #skewness

In calculations of variance we do not know whether large deviations are likely to be positive or negative, hence the degree of symmetry in return distributions.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644785962252

#reading-8-statistical-concepts-and-market-returns #skewness

A return distribution with positive skew has frequent small losses and a few extreme gains. A return distribution with negative skew has frequent small gains and a few extreme losses.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644787797260

#reading-8-statistical-concepts-and-market-returns #skewness

A return distribution with positive skew has frequent small losses and a few extreme gains. A return distribution with negative skew has frequent small gains and a few extreme losses. The positively skewed distribution shown has a long tail on its right side; the negatively skewed distribution has a long tail on its left side. For the positively skewed unimodal distribution, the mode is less than the median, which is less than the mean. For the negatively skewed unimodal distribution, the mean is less than the median, which is less than the mode.41 Investors should be attracted by a positive skew because the mean return falls above the median. Relative to the mean return, positive skew amounts to a limited, though frequent, downside compared with a somewhat unlimited, but less frequent, upside.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644790156556

#reading-8-statistical-concepts-and-market-returns #skewness

If a distribution is positively skewed with a mean greater than its median, then more than half of the deviations from the mean are negative and less than half are positive

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644792777996

#reading-8-statistical-concepts-and-market-returns #skewness

Table 27 shows several summary statistics for the annual and monthly returns on the S&P 500. Earlier we discussed the arithmetic mean return and standard deviation of return, and we shall shortly discuss kurtosis.

Table 27. S&P 500 Annual and Monthly Total Returns, 1926–2012: Summary Statistics

Return Series	Number of Periods	Arithmetic Mean (%)	Standard Deviation (%)	Skewness	Excess Kurtosis
S&P 500 (Annual)	87	11.82	20.18	−0.3768	0.0100
S&P 500 (Monthly)	1,044	0.94	5.50	0.3456	9.4288

Source: Ibbotson Associates.

Table 27 reveals that S&P 500 annual returns during this period were negatively skewed while monthly returns were positively skewed, and the magnitude of skewness was greater for the annual series. We would find for other market series that the shape of the distribution of returns often depends on the holding period examined.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644795923724

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The statistical measure that indicates the peakedness of a distribution.

Answer

Kurtosis

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644797758732

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Describes a distribution that is more peaked than a normal distribution.

Answer

Leptokurtic

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644799593740

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Describes a distribution that is less peaked than the normal distribution.

Answer

Platykurtic

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644801428748

Tags

#reading-8-statistical-concepts-and-market-returns

Question

lepto comes from the Greek word for [...]

Answer

slender

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644803525900

Tags

#reading-8-statistical-concepts-and-market-returns

Question

platy comes from the Greek word for [...]

Answer

broad

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644805360908

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Describes a distribution with kurtosis identical to that of the normal distribution.

Answer

Mesokurtic

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644807720204

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The calculation for kurtosis involves finding the average of deviations from the mean raised to the [...] and then standardizing that average by dividing by the standard deviation raised to the [...]

Answer

fourth power

fourth power

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644809555212

Tags

#reading-8-statistical-concepts-and-market-returns

Question

For all normal distributions, kurtosis is equal to [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644811914508

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Degree of peakedness (fatness of tails) in excess of the peakedness of the normal distribution.

Answer

Excess Kurtosis

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644814011660

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Excess Kurtosis formula

$K_e =$ [...] $ \displaystyle\sum_{i=1}^n(Xi-\bar{X})^4\over {s^4} $$- {3(n-1)^2\over (n-2)(n-3)}$

Answer

$Ke = {n(n+1) \over (n-1)(n-2)(n-3)}$

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644817681676

Tags

#reading-8-statistical-concepts-and-market-returns

Question

For a sample of 100 or larger taken from a normal distribution, a sample excess kurtosis of [...] or larger would be considered unusually large.

Answer

1.0

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644819778828

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Most equity return series have been found to be [...]

(Regarding Kurtosis)

Answer

leptokurtic.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644822662412

#reading-8-statistical-concepts-and-market-returns

With the concepts of descriptive statistics in hand, we will see why the geometric mean is appropriate for making investment statements about past performance. We will also explore why the arithmetic mean is appropriate for making investment statements in a forward-looking context.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644825283852

#reading-8-statistical-concepts-and-market-returns

A semilogarithmic scale describes a scale constructed so that equal intervals on the vertical scale represent equal rates of change, and equal intervals on the horizontal scale represent equal amounts of change.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644831837452

Tags

#reading-9-probability-concepts

Question

A quantity whose future outcomes are uncertain.

Answer

Random variable

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644833672460

Tags

#reading-9-probability-concepts

Question

A possible value of a random variable.

Answer

Outcome

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644835769612

Tags

#reading-9-probability-concepts

Question

Any outcome or specified set of outcomes of a random variable.

Answer

Event

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644837866764

#reading-9-probability-concepts

The return on a risky asset is an example of a random variable, a quantity whose outcomes are uncertain. For example, a portfolio may have a return objective of 10 percent a year. The portfolio manager’s focus at the moment may be on the likelihood of earning a return that is less than 10 percent over the next year. Ten percent is a particular value or outcome of the random variable “portfolio return.” Although we may be concerned about a single outcome, frequently our interest may be in a set of outcomes: The concept of “event” covers both.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644840488204

Tags

#reading-9-probability-concepts

Question

We use [...] to highlight statements that define events.

Answer

italics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644842585356

Tags

#reading-9-probability-concepts

Question

A number between 0 and 1 describing the chance that a stated event will occur.

Answer

Probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644844682508

Tags

#reading-9-probability-concepts

Question

Covering or containing all possible outcomes.

Answer

Exhaustive

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644847041804

Tags

#reading-9-probability-concepts

Question

The probability of an event estimated as a relative frequency of occurrence.

Answer

Empirical probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644849401100

Tags

#reading-9-probability-concepts

Question

A probability drawing on personal or subjective judgment.

Answer

Subjective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644851236108

Tags

#reading-9-probability-concepts

Question

A probability based on logical analysis rather than on observation or personal judgment.

Answer

A priori probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644853071116

Tags

#reading-9-probability-concepts

Question

Probabilities that generally do not vary from person to person; includes a priori and empirical probabilities.

Answer

Objective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644858313996

#investopedia

Antitrust laws prohibit a variety of practices that restrain trade. like price-fixing conspiracies, corporate mergers likely to reduce the competitive vigor of particular markets, and predatory acts designed to achieve or maintain monopoly power.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Antitrust
What is 'Antitrust' Antitrust laws are the laws that apply to virtually all industries and to every level of business, including manufacturing, transportation, distribution and marketing. They prohibit a variety of practices that restrain trade. Examples of illegal practices are price-fixing conspiracies, corporate mergers likely to reduce the competitive vigor of particular markets, and predatory acts designed to achieve or maintain monopoly power. BREAKING DOWN 'Antitrust' Antitrust laws are necessary in an open marketplace. Competition among sellers gives consumers lower prices, higher-quali

Flashcard 1644860935436

Tags

#reading-9-probability-concepts

Question

A trade in two closely related stocks involving the short sale of one and the purchase of the other.

Answer

Pairs arbitrage trade

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644862770444

#reading-9-probability-concepts

Consistent with reference to estimators, describes an estimator for which the probability of estimates close to the value of the population parameter increases as sample size increases.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644864605452

Tags

#reading-9-probability-concepts

Question

A result in probability theory stating that inconsistent probabilities create profit opportunities.

Answer

Dutch book theorem

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644866440460

#reading-9-probability-concepts

The theorem’s name comes from the terminology of wagering. Suppose someone places a $100 bet on X at odds of 10 to 1 against X, and later he is able to place a $600 bet against X at odds of 1 to 1 against X. Whatever the outcome of X, that person makes a riskless profit (equal to $400 if X occurs or $500 if X does not occur) because the implied probabilities are inconsistent. He is said to have made a Dutch book in X. Ramsey (1931) presented the problem of inconsistent probabilities. See also Lo (1999).

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644869061900

Tags

#reading-9-probability-concepts

Question

The probability of an event not conditioned on another event.

Answer

Unconditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644870896908

#reading-9-probability-concepts

In analyses of probabilities presented in tables, unconditional probabilities usually appear at the ends or margins of the table, hence the term marginal probability. Because of possible confusion with the way marginal is used in economics (roughly meaning incremental), we use the term unconditional probabilitythroughout this discussion.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644872731916

Tags

#reading-9-probability-concepts

Question

The probability of an event given (conditioned on) another event.

Answer

Conditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644874829068

#reading-9-probability-concepts

The conditional probability of an event may be greater than, equal to, or less than the unconditional probability, depending on the facts.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644876664076

Tags

#reading-9-probability-concepts

Question

The probability of the joint occurrence of stated events.

Answer

Joint probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644878761228

Tags

#reading-9-probability-concepts

Question

The rule that the joint probability of events A and B equals the probability of A given B times the probability of B.

Answer

Multiplication rule for probabilities

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644880858380

Tags

#reading-9-probability-concepts

Question

The return on a risky asset is an example of a [...]

Answer

random variable,

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644882693388

Tags

#reading-9-probability-concepts

Question

A = the portfolio earns a return of 10 percent

B = the portfolio earns a return below 10 percent.

Which one is an event and which one an outcome?

Answer

A= outcome

B= event

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644884528396

Tags

#reading-9-probability-concepts

Question

A = the portfolio earns a return of 10 percent

B = the portfolio earns a return below 10 percent.

Which one is an event and which one an outcome?

Answer

Both are events but A has only one outcome

A= outcome

B= event

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644886363404

Tags

#reading-9-probability-concepts

Question

it is common to use a [...] to represent a defined event.

Answer

capital letter in italics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644888198412

Tags

#reading-9-probability-concepts

Question

The sum of the probabilities of any set of mutually exclusive and exhaustive events equals [...] .

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644890295564

#reading-9-probability-concepts

If we know both the set of all the distinct possible outcomes of a random variable and the assignment of probabilities to those outcomes—the probability distribution of the random variable—we have a complete description of the random variable, and we can assign a probability to any event that we might describe

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644892130572

Tags

#reading-9-probability-concepts

Question

The probability of any event is the sum of the probabilities of [...]

Answer

the distinct outcomes included in the definition of the event.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644893965580

#reading-9-probability-concepts

Suppose the event of interest is D = the portfolio earns a return above the risk-free rate, and we know the probability distribution of portfolio returns. Assume the risk-free rate is 4 percent. To calculate P(D), the probability of D, we would sum the probabilities of the outcomes that satisfy the definition of the event; that is, we would sum the probabilities of portfolio returns greater than 4 percent.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644895800588

Tags

#reading-9-probability-concepts

Question

there are [...] broad approaches to estimating probabilities

Answer

three

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644897635596

#reading-9-probability-concepts

In investments, we often estimate the probability of an event as a relative frequency of occurrence based on historical data.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644899470604

#reading-9-probability-concepts

Relationships must be stable through time for empirical probabilities to be accurate. We cannot calculate an empirical probability of an event not in the historical record or a reliable empirical probability for a very rare event. There are cases, then, in which we may adjust an empirical probability to account for perceptions of changing relationships. In other cases, we have no empirical probability to use at all. We may also make a personal assessment of probability without reference to any particular data. Each of these three types of probability is a subjective probability, one drawing on personal or subjective judgment

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644901305612

#reading-9-probability-concepts

Subjective probabilities are of great importance in investments. Investors, in making buy and sell decisions that determine asset prices, often draw on subjective probabilities. Subjective probabilities appear in various places in this reading, notably in our discussion of Bayes’ formula.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644903140620

Tags

#reading-9-probability-concepts

Question

Odds for E = [...]

Answer

P(E) / [1 − P(E)]

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644904975628

Tags

#reading-9-probability-concepts

Question

Given odds for E of “a to b,” the implied probability of E is [...]

Answer

a/(a + b).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644907072780

Tags

#reading-9-probability-concepts

Question

Odds against E = [...]

Answer

[1 − P (E) ] / P (E)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644908907788

Tags

#reading-9-probability-concepts

Question

Odds against are the [...] of odds for E

Answer

reciprocal

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644910742796

Tags

#reading-9-probability-concepts

Question

Given odds against E of “a to b,” the implied probability of E is [...]

Answer

b/(a + b).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644912577804

#reading-9-probability-concepts

"1 to 7.” For each occurrence of E, we expect seven cases of non-occurrence; out of eight cases in total, therefore, we expect E to happen once, and the probability of E is 1/8.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644914937100

#reading-9-probability-concepts

For odds of “15 to 1” against E (an implied probability of E of 1/16), a $1 wager on E, if successful, returns $15 in profits plus the $1 staked in the wager.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644916772108

Tags

#reading-9-probability-concepts

Question

To understand the meaning of a probability in investment contexts, we need to distinguish between two types of probability: [...]

Answer

unconditional and conditional.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644918607116

#reading-9-probability-concepts

Suppose the question is “What is the probability that the stock earns a return above the risk-free rate (event A)?” The answer is an unconditional probability that can be viewed as the ratio of two quantities. The numerator is the sum of the probabilities of stock returns above the risk-free rate. Suppose that sum is 0.70. The denominator is 1, the sum of the probabilities of all possible returns. The answer to the question is P(A) = 0.70.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644920442124

Tags

#reading-9-probability-concepts

Question

“What is the probability of this event A?” is an [...]

Answer

unconditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644922277132

Tags

#reading-9-probability-concepts

Question

Unconditional probability is also frequently referred to as [...]

Answer

marginal probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644924898572

Tags

#reading-9-probability-concepts

Question

The denominator in an unconditional probability is [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644926733580

Tags

#reading-9-probability-concepts

Question

The denominator in an conditional probability is [...] of the event that conditions it.

Answer

the sum of the probabilities for all outcomes

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644928830732

Tags

#reading-9-probability-concepts

Question

“What is the probability of A, given that B has occurred?” The probability in answer to this last question is a [...]

Answer

conditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644930665740

#reading-9-probability-concepts

Given additional information on company characteristics, could an investor refine that estimate? Investors continually seek an information edge that will help improve their forecasts. In mathematical terms, they are attempting to frame their view of the future using probabilities conditioned on relevant information or events.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644932500748

Tags

#reading-9-probability-concepts

Question

To state an exact definition of conditional probability, we first need to introduce the concept of [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644934860044

Tags

#reading-9-probability-concepts

Question

“What is the probability of both A and B happening?” The answer to this question is a [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644936695052

Tags

#reading-9-probability-concepts

Question

[...] (read: “the probability of A and B”)

Answer

P(AB)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644938530060

Tags

#reading-9-probability-concepts

Question

The joint probability of A and B is the [...]

Answer

sum of the probabilities of the outcomes they have in common.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644969200908

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The class width is from the [...] to the [...] limit

Answer

lower class limit

lower class

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644971822348

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The [...] for every class is the smallest value in that class.

Answer

lower limit

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644973657356

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The [...] for every class is the greatest value possible in that class.

Answer

upper limit

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644975492364

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Class boundaries are the [...]

Answer

numbers used to separate classes.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644977589516

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The size of the gap between classes is the difference between the [...] of one class and the [...] class.

Answer

upper class limit

lower class limit of the next

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644979424524

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The lower boundary of each class is calculated by [...]

Answer

the class lower limit minus 1/2 of the gap value.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644981259532

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The upper boundary of each class is calculated by [...]

Answer

adding half of the gap value to the class upper limit.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644983880972

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A [...] is the midpoint between two class limits

Answer

class boundary

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644986240268

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Can you tell the maximum and minimun value from observing a frequency distribution?

Answer

Fuck no

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Article 1644992269580

Stem-and-leaf graph
#math-shit

A stem-and-leaf graph, also called a stemplot, is a way to represent the distribution of numeric data. It was invented by John Tukey, a mathematician, and is a quick way to picture data for numbers that are greater than 0. I'll explain using an example. Suppose you have the following set of numbers (they might represent the number of home runs hit by a major league baseball player during his career). 32, 33, 21, 45, 58, 20, 33, 44, 28, 15, 18, 25 The stem of a stemplot can have as many digits as needed, but the leaves should contain only one digit. To create a stemplot to display the above data, you must first create the stem. Since all of the numbers have just two digits, start by arranging the tens digits from smallest to largest. To create the leaves, draw a vertical bar after each of the tens digits and arrange the ones digits from each number in the data set in order from smallest to largest. If there are duplicate numbers, like 33, list each one. 1|58 2|0158

Annotation 1644993580300

#math-shit

A stem-and-leaf graph, also called a stemplot, is a way to represent the distribution of numeric data. It was invented by John Tukey, a mathematician, and is a quick way to picture data for numbers that are greater than 0.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Stem-and-leaf graph
A stem-and-leaf graph, also called a stemplot, is a way to represent the distribution of numeric data. It was invented by John Tukey, a mathematician, and is a quick way to picture data for numbers that are greater than 0. I'll explain using an example. Suppose you have the following set of numbers (they might represent the number of home runs hit by a major league baseball player during

Annotation 1644995153164

#math-shit

The stem of a stemplot can have as many digits as needed, but the leaves should contain only one digit.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Stem-and-leaf graph
Suppose you have the following set of numbers (they might represent the number of home runs hit by a major league baseball player during his career). 32, 33, 21, 45, 58, 20, 33, 44, 28, 15, 18, 25 The stem of a stemplot can have as many digits as needed, but the leaves should contain only one digit. To create a stemplot to display the above data, you must first create the stem. Since all of the numbers have just two digits, start by arranging the tens digits from

Flashcard 1644996726028

Tags

#math-shit

Question

You can find the median by [...] of the stemplot until [...]

Answer

counting from either end

you find its center.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Stem-and-leaf graph
2|0158 3|233 4|45 5|8 The shape of the resulting display looks something like a bar graph oriented vertically. By examining the stemplot, you can determine certain properties of the data. You can find the median by counting from either end of the stemplot until you find its center. Here, since there are 12 numbers, the center lies between 28 and 32. The median is the average of the two data points: (28+32)/2 = 30.) You can also determine if

Flashcard 1645005114636

Tags

#analysts-questions

Question

To find quantiles in a frequency distribution you have to know [...]

Answer

cumulative frequency

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Edited, memorised or added to reading queue

on 24-Jul-2017 (Mon)

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

pdf

pdf

pdf