Edited, memorised or added to reading queue
on 06-Jan-2018 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1621391707404
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1622690106636
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1622926036236
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1632002510092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 3. Dollar-weighted and Time-weighted Rates of Return
sub-period: HPR = (Dividends + Ending Price)/Beginning Price - 1. For the first year, HPR 1 : (150 + 10)/100 - 1 = 0.60. For the second year, HPR 2 : (280 + 20)/300 - 1 = 0. Calculate the time-weighted rate of return: <span>If the measurement period < 1 year, compound holding period returns to get an annualized rate of return for the year. If the measurement period > 1 year, take the geometric mean of the annual returns. <span><body><html>
Flashcard 1633798982924
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA zero-coupon bond is a debt security that doesn't pay interest (a coupon) but is traded at a deep discount, rendering profit at maturity when the bond is redeemed for its full face value.
Original toplevel document
Zero-Coupon BondWhat is a 'Zero-Coupon Bond' <span>A zero-coupon bond, also known as an "accrual bond," is a debt security that doesn't pay interest (a coupon) but is traded at a deep discount, rendering profit at maturity when the bond is redeemed for its full face value. Some zero-coupon bonds are issued as such, while others are bonds that have been stripped of their coupons by a financial institution and then repackaged as zero-coupon bonds. Because t
Flashcard 1633877101836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 5. Bond Equivalent Yield
Periodic bond yields for both straight and zero-coupon bonds are conventionally computed based on semi-annual periods, as U.S. bonds typically make two coupon payments per year. For example, a zero-coupon bond with a maturity of five years will mature in 10 6-month periods. The periodic yield for that bond, r, is indicated by the equation Price = Maturity value x (1 + r) -10 . This yield is an internal rate of return with semi-annual compounding. How do we
Flashcard 1634542161164
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1635099741452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1635107081484
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1635136179468
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1635224521996
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1635444722956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 2. Measurement Scales
ing and addition or subtraction, ratio scales allow computation of meaningful ratios. A good example is the Kelvin scale of temperature. This scale has an absolute zero. Thus, a temperature of 300°K is twice as high as a temperature of 150°K. <span>Two financial examples of ratio scales are rates of return and money. Both examples can be measured on a zero scale, where zero represents no return, or in the case of money, no money. Note that as you move down through this list, the measur
Flashcard 1636650061068
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 4. Measures of Center Tendency
of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: <span>The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while th
Flashcard 1636864232716
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1637115890956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1641175190796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1644907072780
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1645856558348
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itDollar-cost averaging (DCA) is an investment technique of buying a fixed dollar amount of a particular investment on a regular schedule, regardless of the share price. The investor purchases more shares when prices are low and fewer shares when prices are high. The premise is that DCA lowers the average share cost over time, increasing the opportunity
Original toplevel document
Dollar-Cost Averaging (DCA)What is 'Dollar-Cost Averaging - DCA' <span>Dollar-cost averaging (DCA) is an investment technique of buying a fixed dollar amount of a particular investment on a regular schedule, regardless of the share price. The investor purchases more shares when prices are low and fewer shares when prices are high. The premise is that DCA lowers the average share cost over time, increasing the opportunity to profit. The DCA technique does not guarantee that an investor won't lose money on investments. Rather, it is meant to allow investment over time instead of investment as a lump sum. BREAKING DOWN 'Dollar-Cost Averaging - DCA' Fundamental to the strategy is a commitment to investing a fixed dollar amount each month. Depending
Flashcard 1646434585868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 6. Expected Value, Variance, and Standard Deviation of a Random Variable
ed with probability, the expected value simply factors in the relative chances of each event occurring, in order to determine the overall result. The more probable outcomes will have a greater weighting in the overall calculation. <span>For a random variable X, the expected value of X is denoted E(X). E(X) = P(x 1 ) x 1 + P(x 2 ) x 2 + ... + P(x n ) x n In investment analysis, forecasts are frequently made using expected value, for example,
ed with probability, the expected value simply factors in the relative chances of each event occurring, in order to determine the overall result. The more probable outcomes will have a greater weighting in the overall calculation. <span>For a random variable X, the expected value of X is denoted E(X). E(X) = P(x 1 ) x 1 + P(x 2 ) x 2 + ... + P(x n ) x n In investment analysis, forecasts are frequently made using expected value, for example,
Flashcard 1646645611788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Ex-Ante
What is 'Ex-Ante' <span>Ex-ante, derived from the Latin for "before the event," is a term that refers to future events, such as future returns or prospects of a company. Ex-ante analysis helps to give an idea of future movements in price or the future impact of a n
What is 'Ex-Ante' <span>Ex-ante, derived from the Latin for "before the event," is a term that refers to future events, such as future returns or prospects of a company. Ex-ante analysis helps to give an idea of future movements in price or the future impact of a n
Flashcard 1646689914124
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn easier way to interpret expected value is as follows: If a number of such concerts were held, the organizers can expect to achieve a profit of $14,000 for each concert. So expected values actually make more sense when viewed over the long run.
Original toplevel document
Subject 6. Expected Value, Variance, and Standard Deviation of a Random Variablefit that will be made the remaining 50% of the time more than offsets this and creates an overall expected profit. However, with a one-off concert, there is a major risk involved, particularly in the event of unfavorable weather. <span>An easier way to interpret expected value is as follows: If a number of such concerts were held, the organizers can expect to achieve a profit of $14,000 for each concert. So expected values actually make more sense when viewed over the long run. The variance of a random variable is the expected value (the probability-weighted average) of squared deviations from the random variable's expected value. &
Flashcard 1648858631436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 8. Portfolio Expected Return and Variance
The expected return on a portfolio of assets is the market-weighted average of the expected returns on the individual assets in the portfolio. The variance of a portfolio's return consists of two components: the weighted average of the variance for individual assets and the weighted covariance between pairs of individual asset
The expected return on a portfolio of assets is the market-weighted average of the expected returns on the individual assets in the portfolio. The variance of a portfolio's return consists of two components: the weighted average of the variance for individual assets and the weighted covariance between pairs of individual asset
Flashcard 1648872787212
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1648875146508
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1648910273804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1652123897100
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 10. Principles of Counting
nlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or t
nlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or t
Flashcard 1652318407948
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652320242956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652323912972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data
Original toplevel document
the+empirical+rule - Buscar con Googlertment of Statistics Online Learning! - Penn State","th":83,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcQuElAJ2v_EaT3kTk6OttMFj8vC8cwGQrbEbwExrMxvAB-IY7aQ1Nkvdoo","tw":210} <span>The empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data falls within the first standard deviation from the mean. 95% fall within two standard deviations.Nov 1, 2013 Empirical Rule: What is it? - Statistics How To www.statisticshowto.com/empirical-rule-2/ Feedback About this result People also ask What is the empirical rul
Flashcard 1652329155852
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Sequential comparisons of quarterly EPS are with the immediate prior quarter. A sequential comparison stands in contrast to a comparison with the same quarter one year ago (another frequent type o
Flashcard 1652335971596
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Multinomial Formula (General Formula for Labeling Problems). The number of ways that n objects can be labeled with kdifferent labels, with n 1 of the first type, n 2 of the second type, and so on, with n
Flashcard 1652344622348
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):
Original toplevel document
Subject 10. Principles of Countingnlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
Flashcard 1652379487500
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Multinominal formula
A mutual fund guide ranked 18 bond mutual funds by total returns for the year 2014. The guide also assigned each fund one of five risk labels: high risk (four funds), above-average risk (
Flashcard 1652389448972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
ossible outcomes? If the answer is yes, you may be able to use a tool in this section, and you can go to the second question. If the answer is no, the number of outcomes is infinite, and the tools in this section do not apply. <span>Do I want to assign every member of a group of size n to one of n slots (or tasks)? If the answer is yes, use n factorial. If the answer is no, go to the third question. Do I want to count the number of ways to apply one of three or more labels to each member of a group? If the answer is yes
Flashcard 1652393381132
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
the tools in this section do not apply. Do I want to assign every member of a group of size n to one of n slots (or tasks)? If the answer is yes, use n factorial. If the answer is no, go to the third question. <span>Do I want to count the number of ways to apply one of three or more labels to each member of a group? If the answer is yes, use the multinomial formula. If the answer is no, go to the fourth question. Do I want to count the number of ways that I can choose r objects from a total of n, when the order in which I list the r
Flashcard 1652398361868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
al of n, when the order in which I list the r objects does not matter (can I give the r objects a label)? If the answer to these questions is yes, the combination formula applies. If the answer is no, go to the fifth question. <span>Do I want to count the number of ways I can choose r objects from a total of n, when the order in which I list the r objects is important? If the answer is yes, the permutation formula applies. If the answer is no, go to question 6. Can the multiplication rule of counting be used? If it cannot, you may have to count the possibilities one by one, or use more adv
Flashcard 1654675344652
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1729401589004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itad><head> By leveraging stochastic processes such as the beta and Dirichlet process (DP), these methods allow the data to drive the complexity of the learned model, while still permit- ting efficient inference algorithms. <html>
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1729419676940
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAlmost all machine-learning tasks can be formulated as making inferences about missing or latent data from the observed data
Original toplevel document (pdf)
cannot see any pdfsFlashcard 1729421249804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Flashcard 1729425444108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Negative binomial distribution - Wikipedia
) 2 ( p ) {\displaystyle {\frac {r}{(1-p)^{2}(p)}}} <span>In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures (denoted r) occurs. For example, if we define a 1 as failure, all non-1s as successes, and we throw a dice repeatedly until the third time 1 appears (r = three failures), then the probability distribution
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Negative binomial distribution - Wikipedia
) . {\displaystyle \operatorname {Poisson} (\lambda )=\lim _{r\to \infty }\operatorname {NB} \left(r,{\frac {\lambda }{\lambda +r}}\right).} Gamma–Poisson mixture[edit source] <span>The negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed as a gamma distribution with shape = r and scale θ = p/(1 − p) or correspondingly rate β = (1 − p)/p. To display the intuition behind this statement, consider two independent Poisson processes, “Success” and “Failure”, with intensities p and 1 − p. Together, the Success and Failure pr
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
a }}\mathbf {t} {\Big )}} In probability theory and statistics, the multivariate normal distribution or multivariate Gaussian distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. <span>One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly)
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
e definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. <span>The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Contents [hide] 1 Notation and parametrization 2 Definition 3 Properties 3.1 Density function 3.1.1 Non-degenerate case 3.1.2 Degenerate case 3.2 Higher moments 3.3 Lik
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
al {CN}}_{0}\|{\mathcal {CN}}_{1})=\operatorname {tr} \left({\boldsymbol {\Sigma }}_{1}^{-1}{\boldsymbol {\Sigma }}_{0}\right)-k+\ln {|{\boldsymbol {\Sigma }}_{1}| \over |{\boldsymbol {\Sigma }}_{0}|}.} Mutual information[edit source] <span>The mutual information of a distribution is a special case of the Kullback–Leibler divergence in which P {\displaystyle P} is the full multivariate distribution and Q {\displaystyle Q} is the product of the 1-dimensional marginal distributions. In the notation of the Kullback–Leibler divergence section of this article, Σ 1
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
ldsymbol {\rho }}_{0}} is the correlation matrix constructed from Σ 0 {\displaystyle {\boldsymbol {\Sigma }}_{0}} . <span>In the bivariate case the expression for the mutual information is: I ( x ; y ) = − 1 2 ln ( 1 − ρ 2 ) . {\displaystyle I(x;y)=-{1 \over 2}\ln(1-\rho ^{2}).} Cumulative distribution function[edit source] The notion of cumulative distribution function (cdf) in dimension 1 can be extended in two ways to the multidimensional case, based
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Generalized inverse - Wikipedia
ree encyclopedia Jump to: navigation, search "Pseudoinverse" redirects here. For the Moore–Penrose inverse, sometimes referred to as "the pseudoinverse", see Moore–Penrose inverse. <span>In mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A {\displaystyle A} . Formally, given a matrix A ∈
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Generalized inverse - Wikipedia
nverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A {\displaystyle A} . <span>Formally, given a matrix A ∈ R n × m {\displaystyle A\in \mathbb {R} ^{n\times m}} and a matrix A g ∈ R m × n {\displaystyle A^{\mathrm {g} }\in \mathbb {R} ^{m\times n}} , A g {\displaystyle A^{\mathrm {g} }} is a generalized inverse of A {\displaystyle A} if it satisfies the condition A A g A = A {\displaystyle AA^{\mathrm {g} }A=A} . [1] [2] [3] The purpose of constructing a generalized inverse of a matrix is to obtain a matrix that can serve as an inverse in some sense for a wider class of matrices than invertibl
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Moore–Penrose inverse - Wikipedia
tegral operators in 1903. When referring to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose inverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse. <span>A common use of the pseudoinverse is to compute a 'best fit' (least squares) solution to a system of linear equations that lacks a unique solution (see below under § Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. The pseudoinverse facilitates the
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Moore–Penrose inverse - Wikipedia
tion (see below under § Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. The pseudoinverse facilitates the statement and proof of results in linear algebra. <span>The pseudoinverse is defined and unique for all matrices whose entries are real or complex numbers. It can be computed using the singular value decomposition. Contents [hide] 1 Notation 2 Definition 3 Properties 3.1 Existence and uniqueness 3.2 Basic properties 3.2.1 Identities 3.3 Reduction to Hermitian case 3.4 Products 3.5
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Moore–Penrose inverse - Wikipedia
; K ) {\displaystyle I_{n}\in \mathrm {M} (n,n;K)} denotes the n × n {\displaystyle n\times n} identity matrix. Definition[edit source] <span>For A ∈ M ( m , n ; K ) {\displaystyle A\in \mathrm {M} (m,n;K)} , a pseudoinverse of A {\displaystyle A} is defined as a matrix A + ∈ M ( n , m ; K ) {\displaystyle A^{+}\in \mathrm {M} (n,m;K)} satisfying all of the following four criteria: [8] [9] A A + A = A {\displaystyle AA^{+}A=A\,\!} (AA + need not be the general identity matrix, but it maps all column vectors of A to themselves); A + A A + = A + {\displaystyle A^{+}AA^{+}=A^{+}\,\!} (A + is a weak inverse for the multiplicative semigroup); ( A A + ) ∗ = A A + {\displaystyle (AA^{+})^{*}=AA^{+}\,\!} (AA + is Hermitian); and ( A + A ) ∗ = A + A {\displaystyle (A^{+}A)^{*}=A^{+}A\,\!} (A + A is also Hermitian). A + {\displaystyle A^{+}} exists for any matrix A {\displaystyle A} , but when the latter has full rank, A + {\displaystyle A^{+}} can be expressed as a simple algebraic formula. In particular, when A {\displaystyle A} has linearly independent columns (and thus matrix A ∗ A {\displaystyle A^{*}A} is invertible), A + {\displaystyle A^{+}} can be computed as: A + = ( A ∗ A ) − 1 A ∗ . {\displaystyle A^{+}=(A^{*}A)^{-1}A^{*}\,.} This particular pseudoinverse constitutes a left inverse, since, in this case, A + A = I {\displaystyle A^{+}A=I} . When A {\displaystyle A} has linearly independent rows (matrix A A ∗ {\displaystyle AA^{*}} is invertible), A + {\displaystyle A^{+}} can be computed as: A + = A ∗ ( A A ∗ ) − 1 . {\displaystyle A^{+}=A^{*}(AA^{*})^{-1}\,.} This is a right inverse, as A A + = I {\displaystyle AA^{+}=I} . Properties[edit source] Proofs for some of these facts may be found on a separate page Proofs involving the Moore–Penrose inverse. Existence and uniqueness[edit source] The pseu
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
y two or more of its components that are pairwise independent are independent. But, as pointed out just above, it is not true that two random variables that are (separately, marginally) normally distributed and uncorrelated are independent. <span>Conditional distributions[edit source] If N-dimensional x is partitioned as follows x = [ x 1 x 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle \mathbf {x} ={\begin{bmatrix}\mathbf {x} _{1}\\\mathbf {x} _{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} and accordingly μ and Σ are partitioned as follows μ = [ μ 1 μ 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle {\boldsymbol {\mu }}={\begin{bmatrix}{\boldsymbol {\mu }}_{1}\\{\boldsymbol {\mu }}_{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] with sizes [ q × q q × ( N − q ) ( N − q ) × q ( N − q ) × ( N − q ) ] {\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{12}\\{\boldsymbol {\Sigma }}_{21}&{\boldsymbol {\Sigma }}_{22}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times q&q\times (N-q)\\(N-q)\times q&(N-q)\times (N-q)\end{bmatrix}}} then the distribution of x 1 conditional on x 2 = a is multivariate normal (x 1 | x 2 = a) ~ N(μ, Σ) where μ ¯ = μ 1 + Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\bar {\boldsymbol {\mu }}}={\boldsymbol {\mu }}_{1}+{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} and covariance matrix Σ ¯ = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 . {\displaystyle {\overline {\boldsymbol {\Sigma }}}={\boldsymbol {\Sigma }}_{11}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}{\boldsymbol {\Sigma }}_{21}.} [13] This matrix is the Schur complement of Σ 22 in Σ. This means that to calculate the conditional covariance matrix, one inverts the overall covariance matrix, drops the rows and columns corresponding to the variables being conditioned upon, and then inverts back to get the conditional covariance matrix. Here Σ 22 − 1 {\displaystyle {\boldsymbol {\Sigma }}_{22}^{-1}} is the generalized inverse of Σ 22 {\displaystyle {\boldsymbol {\Sigma }}_{22}} . Note that knowing that x 2 = a alters the variance, though the new variance does not depend on the specific value of a; perhaps more surprisingly, the mean is shifted by Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} ; compare this with the situation of not knowing the value of a, in which case x 1 would have distribution N q ( μ 1 , Σ 11 ) {\displaystyle {\mathcal {N}}_{q}\left({\boldsymbol {\mu }}_{1},{\boldsymbol {\Sigma }}_{11}\right)} . An interesting fact derived in order to prove this result, is that the random vectors x 2 {\displaystyle \mathbf {x} _{2}} and y 1 = x 1 − Σ 12 Σ 22 − 1 x 2 {\displaystyle \mathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}} are independent. The matrix Σ 12 Σ 22 −1 is known as the matrix of regression coefficients. Bivariate case[edit source] In the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is [14]
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
) {\displaystyle \operatorname {E} (X_{1}\mid X_{2}##BAD TAG##\rho E(X_{2}\mid X_{2}##BAD TAG##} and then using the properties of the expectation of a truncated normal distribution. Marginal distributions[edit source] <span>To obtain the marginal distribution over a subset of multivariate normal random variables, one only needs to drop the irrelevant variables (the variables that one wants to marginalize out) from the mean vector and the covariance matrix. The proof for this follows from the definitions of multivariate normal distributions and linear algebra. [16] Example Let X = [X 1 , X 2 , X 3 ] be multivariate normal random variables with mean vector μ = [μ 1 , μ 2 , μ 3 ] and covariance matrix Σ (standard parametrization for multivariate
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
{\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}} . Affine transformation[edit source] <span>If Y = c + BX is an affine transformation of X ∼ N ( μ , Σ ) , {\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}),} where c is an M × 1 {\displaystyle M\times 1} vector of constants and B is a constant M × N {\displaystyle M\times N} matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB T i.e., Y ∼ N ( c + B μ , B Σ B T ) {\displaystyle \mathbf {Y} \sim {\mathcal {N}}\left(\mathbf {c} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} {\boldsymbol {\Sigma }}\mathbf {B} ^{\rm {T}}\right)} . In particular, any subset of the X i has a marginal distribution that is also multivariate normal. To see this, consider the following example: to extract the subset (X 1 , X 2 , X 4 )
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
implies that the variance of the dot product must be positive. An affine transformation of X such as 2X is not the same as the sum of two independent realisations of X. Geometric interpretation[edit source] See also: Confidence region <span>The equidensity contours of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean. [17] Hence the multivariate normal distribution is an example of the class of elliptical distributions. The directions of the principal axes of the ellipsoids are given by the eigenvec
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
urs of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean. [17] Hence the multivariate normal distribution is an example of the class of elliptical distributions. <span>The directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix Σ. The squared relative lengths of the principal axes are given by the corresponding eigenvalues. If Σ = UΛU T = UΛ 1/2 (UΛ 1/2 ) T is an eigendecomposition where the columns of U are unit eigenvectors and Λ is a diagonal matrix of the eigenvalues, then we have
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
{\mu }}+\mathbf {U} {\mathcal {N}}(0,{\boldsymbol {\Lambda }}).} Moreover, U can be chosen to be a rotation matrix, as inverting an axis does not have any effect on N(0, Λ), but inverting a column changes the sign of U's determinant. <span>The distribution N(μ, Σ) is in effect N(0, I) scaled by Λ 1/2 , rotated by U and translated by μ. Conversely, any choice of μ, full rank matrix U, and positive diagonal entries Λ i yields a non-singular multivariate normal distribution. If any Λ i is zero and U is square, the re
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Ellipsoid - Wikipedia
= 1 : {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:} sphere (top, a=b=c=4), spheroid (bottom left, a=b=5, c=3), tri-axial ellipsoid (bottom right, a=4.5, b=6, c=3) <span>An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface, that is a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is char
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Affine transformation - Wikipedia
s related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Eigendecomposition of a matrix - Wikipedia
| ocultar ahora Eigendecomposition of a matrix From Wikipedia, the free encyclopedia (Redirected from Eigendecomposition) Jump to: navigation, search <span>In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. Contents [hide] 1 Fundamental theory of matrix eigenvectors and eigenvalues 2 Eigendecomposition of a matrix 2.1 Example 2.2 Matrix inverse via eigendecomposition 2.2.1 Pr
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Eigendecomposition of a matrix - Wikipedia
, {\displaystyle v_{i}\,\,(i=1,\dots ,N),} can also be used as the columns of Q. That can be understood by noting that the magnitude of the eigenvectors in Q gets canceled in the decomposition by the presence of Q −1 . <span>The decomposition can be derived from the fundamental property of eigenvectors: A v = λ v {\displaystyle \mathbf {A} \mathbf {v} =\lambda \mathbf {v} } and thus A Q = Q Λ {\displaystyle \mathbf {A} \mathbf {Q} =\mathbf {Q} \mathbf {\Lambda } } which yields A = Q Λ Q − 1 {\displaystyle \mathbf {A} =\mathbf {Q} \mathbf {\Lambda } \mathbf {Q} ^{-1}} . Example[edit source] Taking a 2 × 2 real matrix A = [
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
f them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. <span>Viewed as a machine-learning algorithm, a Gaussian process uses lazy learning and a measure of the similarity between points (the kernel function) to predict the value for an unseen point from training data. The prediction is not just an estimate for that point, but also has uncertainty information—it is a one-dimensional Gaussian distribution (which is the marginal distribution at that poi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Characteristic function (probability theory) - Wikipedia
aracteristic function of a uniform U(–1,1) random variable. This function is real-valued because it corresponds to a random variable that is symmetric around the origin; however characteristic functions may generally be complex-valued. I<span>n probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides the basis of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Characteristic function (probability theory) - Wikipedia
c around the origin; however characteristic functions may generally be complex-valued. In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. <span>If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There ar
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Fourier transform - Wikipedia
ctions for the group of translations. Fourier transforms Continuous Fourier transform Fourier series Discrete-time Fourier transform Discrete Fourier transform Discrete Fourier transform over a ring Fourier analysis Related transforms <span>The Fourier transform (FT) decomposes a function of time (a signal) into the frequencies that make it up, in a way similar to how a musical chord can be expressed as the frequencies (or pitches) of its constituent notes. The Fourier transform of a function of time itself is a complex-value
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Fourier transform - Wikipedia
ctions for the group of translations. Fourier transforms Continuous Fourier transform Fourier series Discrete-time Fourier transform Discrete Fourier transform Discrete Fourier transform over a ring Fourier analysis Related transforms <span>The Fourier transform (FT) decomposes a function of time (a signal) into the frequencies that make it up, in a way similar to how a musical chord can be expressed as the frequencies (or pitches) of its constituent notes. The Fourier transform of a function of time itself is a complex-value
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
μ ℓ {\displaystyle \mu _{\ell }} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] <span>A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of t
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, <span>if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] Stationarity refers to the process' beha
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
initeness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] <span>Stationarity refers to the process' behaviour regarding the separation of any two points x and x' . If the process is stationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. If the process depends only on |x − x'|, the Euclidean distance (not the dire
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
stationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
r the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] <span>If we expect that for "near-by" input points x and x' their corresponding output points y and y' to be "near-by" also, then the assumption of continuity is present. If we wish to allow for significant displacement then we might choose a rougher covariance function. Extreme examples of the behaviour is the Ornstein–Uhlenbeck covariance function and
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
en we might choose a rougher covariance function. Extreme examples of the behaviour is the Ornstein–Uhlenbeck covariance function and the squared exponential where the former is never differentiable and the latter infinitely differentiable. <span>Periodicity refers to inducing periodic patterns within the behaviour of the process. Formally, this is achieved by mapping the input x to a two dimensional vector u(x) = (cos(x), sin(x)). Usual covariance functions[edit source] [imagelink] The effect of choosing different kernels on the prior function distribution of the Gaussian process. Left is a squared expon
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Gaussian process - Wikipedia
{\displaystyle \nu } and Γ ( ν ) {\displaystyle \Gamma (\nu )} is the gamma function evaluated at ν {\displaystyle \nu } . <span>Importantly, a complicated covariance function can be defined as a linear combination of other simpler covariance functions in order to incorporate different insights about the data-set at hand. Clearly, the inferential results are dependent on the values of the hyperparameters θ (e.g. ℓ and σ) defining the model's behaviour. A popular choice for θ is to provide maximum a pos
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Multivariate normal distribution - Wikipedia
mathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}} are independent. The matrix Σ 12 Σ 22 −1 is known as the matrix of regression coefficients. Bivariate case[edit source] <span>In the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is [14] X 1 ∣ X 2 = x 2 ∼ N ( μ 1 + σ 1 σ 2 ρ ( x 2 − μ 2 ) , ( 1 − ρ 2 ) σ 1 2 ) . {\displaystyle X_{1}\mid X_{2}=x_{2}\ \sim \ {\mathcal {N}}\left(\mu _{1}+{\frac {\sigma _{1}}{\sigma _{2}}}\rho (x_{2}-\mu _{2}),\,(1-\rho ^{2})\sigma _{1}^{2}\right).} where ρ {\displaystyle \rho } is the correlation coefficient between X 1 and X 2 . Bivariate conditional expectation[edit source] In the general case[edit source] (
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Indian buffet process - Wikipedia
among the columns in Z {\displaystyle Z} . The parameter α {\displaystyle \alpha } controls the expected number of features present in each observation. <span>In the Indian buffet process, the rows of Z {\displaystyle Z} correspond to customers and the columns correspond to dishes in an infinitely long buffet. The first customer takes the first P o i s s o n ( α )
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Harmonic number - Wikipedia
γ + ln ( x ) {\displaystyle \gamma +\ln(x)} (blue line) where γ {\displaystyle \gamma } is the Euler–Mascheroni constant. <span>In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers: H n = 1 + 1 2 + 1 3 + ⋯ + 1 n = ∑ k = 1 n 1 k . {\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}.} Harmonic numbers are related to the harmonic mean in that the n-th harmonic number is also n times the reciprocal of the harmonic mean of the first n positive integers. Harmonic
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Stationary process - Wikipedia
rting. In the latter case of a deterministic trend, the process is called a trend stationary process, and stochastic shocks have only transitory effects after which the variable tends toward a deterministically evolving (non-constant) mean. <span>A trend stationary process is not strictly stationary, but can easily be transformed into a stationary process by removing the underlying trend, which is solely a function of time. Similarly, processes with one or more unit roots can be made stationary through differencing. An important type of non-stationary process that does not include a trend-like behavior is
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Stationary process - Wikipedia
deterministically evolving (non-constant) mean. A trend stationary process is not strictly stationary, but can easily be transformed into a stationary process by removing the underlying trend, which is solely a function of time. Similarly, <span>processes with one or more unit roots can be made stationary through differencing. An important type of non-stationary process that does not include a trend-like behavior is a cyclostationary process, which is a stochastic process that varies cyclically with time.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Mean reversion (finance) - Wikipedia
ocultar ahora Mean reversion (finance) From Wikipedia, the free encyclopedia Jump to: navigation, search For other uses, see Mean reversion (disambiguation). <span>In finance, mean reversion is the assumption that a stock's price will tend to move to the average price over time. [1] [2] Using mean reversion in stock price analysis involves both identifying the trading range for a stock and computing the average price using analytical techniques taking into ac
Flashcard 1729595837708
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn finance, mean reversion is the assumption that a stock's price will tend to move to the average price over time.
Original toplevel document
Mean reversion (finance) - Wikipediaocultar ahora Mean reversion (finance) From Wikipedia, the free encyclopedia Jump to: navigation, search For other uses, see Mean reversion (disambiguation). <span>In finance, mean reversion is the assumption that a stock's price will tend to move to the average price over time. [1] [2] Using mean reversion in stock price analysis involves both identifying the trading range for a stock and computing the average price using analytical techniques taking into ac
Flashcard 1729597410572
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itprocesses with one or more unit roots can be made stationary through differencing.
Original toplevel document
Stationary process - Wikipediadeterministically evolving (non-constant) mean. A trend stationary process is not strictly stationary, but can easily be transformed into a stationary process by removing the underlying trend, which is solely a function of time. Similarly, <span>processes with one or more unit roots can be made stationary through differencing. An important type of non-stationary process that does not include a trend-like behavior is a cyclostationary process, which is a stochastic process that varies cyclically with time.
Flashcard 1729598983436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA trend stationary process is not strictly stationary, but can easily be transformed into a stationary process by removing the underlying trend, which is solely a function of time.
Original toplevel document
Stationary process - Wikipediarting. In the latter case of a deterministic trend, the process is called a trend stationary process, and stochastic shocks have only transitory effects after which the variable tends toward a deterministically evolving (non-constant) mean. <span>A trend stationary process is not strictly stationary, but can easily be transformed into a stationary process by removing the underlying trend, which is solely a function of time. Similarly, processes with one or more unit roots can be made stationary through differencing. An important type of non-stationary process that does not include a trend-like behavior is
Flashcard 1729601342732
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:
Original toplevel document
Harmonic number - Wikipediaγ + ln ( x ) {\displaystyle \gamma +\ln(x)} (blue line) where γ {\displaystyle \gamma } is the Euler–Mascheroni constant. <span>In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers: H n = 1 + 1 2 + 1 3 + ⋯ + 1 n = ∑ k = 1 n 1 k . {\displaystyle H_{n}=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}}.} Harmonic numbers are related to the harmonic mean in that the n-th harmonic number is also n times the reciprocal of the harmonic mean of the first n positive integers. Harmonic
Flashcard 1729603702028
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn the Indian buffet process, the rows of correspond to customers and the columns correspond to dishes in an infinitely long buffet.
Original toplevel document
Indian buffet process - Wikipediaamong the columns in Z {\displaystyle Z} . The parameter α {\displaystyle \alpha } controls the expected number of features present in each observation. <span>In the Indian buffet process, the rows of Z {\displaystyle Z} correspond to customers and the columns correspond to dishes in an infinitely long buffet. The first customer takes the first P o i s s o n ( α )
Flashcard 1729607109900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is where is the correlation coefficient between X 1 and X 2 .
Original toplevel document
Multivariate normal distribution - Wikipediamathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}} are independent. The matrix Σ 12 Σ 22 −1 is known as the matrix of regression coefficients. Bivariate case[edit source] <span>In the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is [14] X 1 ∣ X 2 = x 2 ∼ N ( μ 1 + σ 1 σ 2 ρ ( x 2 − μ 2 ) , ( 1 − ρ 2 ) σ 1 2 ) . {\displaystyle X_{1}\mid X_{2}=x_{2}\ \sim \ {\mathcal {N}}\left(\mu _{1}+{\frac {\sigma _{1}}{\sigma _{2}}}\rho (x_{2}-\mu _{2}),\,(1-\rho ^{2})\sigma _{1}^{2}\right).} where ρ {\displaystyle \rho } is the correlation coefficient between X 1 and X 2 . Bivariate conditional expectation[edit source] In the general case[edit source] (
Flashcard 1729609469196
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itImportantly, a complicated covariance function can be defined as a linear combination of other simpler covariance functions in order to incorporate different insights about the data-set at hand.
Original toplevel document
Gaussian process - Wikipedia{\displaystyle \nu } and Γ ( ν ) {\displaystyle \Gamma (\nu )} is the gamma function evaluated at ν {\displaystyle \nu } . <span>Importantly, a complicated covariance function can be defined as a linear combination of other simpler covariance functions in order to incorporate different insights about the data-set at hand. Clearly, the inferential results are dependent on the values of the hyperparameters θ (e.g. ℓ and σ) defining the model's behaviour. A popular choice for θ is to provide maximum a pos
Flashcard 1729611042060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itPeriodicity refers to inducing periodic patterns within the behaviour of the process. Formally, this is achieved by mapping the input x to a two dimensional vector u(x) = (cos(x), sin(x)).
Original toplevel document
Gaussian process - Wikipediaen we might choose a rougher covariance function. Extreme examples of the behaviour is the Ornstein–Uhlenbeck covariance function and the squared exponential where the former is never differentiable and the latter infinitely differentiable. <span>Periodicity refers to inducing periodic patterns within the behaviour of the process. Formally, this is achieved by mapping the input x to a two dimensional vector u(x) = (cos(x), sin(x)). Usual covariance functions[edit source] [imagelink] The effect of choosing different kernels on the prior function distribution of the Gaussian process. Left is a squared expon
Flashcard 1729612614924
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf we expect that for "near-by" input points x and x' their corresponding output points y and y' to be "near-by" also, then the assumption of continuity is present.
Original toplevel document
Gaussian process - Wikipediar the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] <span>If we expect that for "near-by" input points x and x' their corresponding output points y and y' to be "near-by" also, then the assumption of continuity is present. If we wish to allow for significant displacement then we might choose a rougher covariance function. Extreme examples of the behaviour is the Ornstein–Uhlenbeck covariance function and
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itIf the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the be
Original toplevel document
Gaussian process - Wikipediastationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
Flashcard 1729615760652
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic.
Original toplevel document
Gaussian process - Wikipediastationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
Flashcard 1729617333516
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic.
Original toplevel document
Gaussian process - Wikipediastationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itIf the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer.
Original toplevel document
Gaussian process - Wikipediastationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
Flashcard 1729620479244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of <span>the observer. <span><body><html>
Original toplevel document
Gaussian process - Wikipediastationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. <span>If the process depends only on |x − x'|, the Euclidean distance (not the direction) between x and x', then the process is considered isotropic. A process that is concurrently stationary and isotropic is considered to be homogeneous; [7] in practice these properties reflect the differences (or rather the lack of them) in the behaviour of the process given the location of the observer. Ultimately Gaussian processes translate as taking priors on functions and the smoothness of these priors can be induced by the covariance function. [5] If we expect that for "ne
Flashcard 1729622052108
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ity> Stationarity refers to the process' behaviour regarding the separation of any two points x and x' . If the process is stationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. <body><html>
Original toplevel document
Gaussian process - Wikipediainiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] <span>Stationarity refers to the process' behaviour regarding the separation of any two points x and x' . If the process is stationary, it depends on their separation, x − x', while if non-stationary it depends on the actual position of the points x and x'. For example, the special case of an Ornstein–Uhlenbeck process, a Brownian motion process, is stationary. If the process depends only on |x − x'|, the Euclidean distance (not the dire
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itif a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion.
Original toplevel document
Gaussian process - Wikipedia} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, <span>if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] Stationarity refers to the process' beha
Flashcard 1729625197836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itif a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour.
Original toplevel document
Gaussian process - Wikipedia} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, <span>if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] Stationarity refers to the process' beha
Flashcard 1729626770700
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open ithead> if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. <html>
Original toplevel document
Gaussian process - Wikipedia} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, <span>if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of this function enables its spectral decomposition using the Karhunen–Loeve expansion. Basic aspects that can be defined through the covariance function are the process' stationarity, isotropy, smoothness and periodicity. [5] [6] Stationarity refers to the process' beha
Flashcard 1729628343564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA key fact of Gaussian processes is that they can be completely defined by their second-order statistics.
Original toplevel document
Gaussian process - Wikipediaμ ℓ {\displaystyle \mu _{\ell }} can be shown to be the covariances and means of the variables in the process. [3] Covariance functions[edit source] <span>A key fact of Gaussian processes is that they can be completely defined by their second-order statistics. [4] Thus, if a Gaussian process is assumed to have mean zero, defining the covariance function completely defines the process' behaviour. Importantly the non-negative definiteness of t
Flashcard 1729630178572
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe Fourier transform (FT) decomposes a function of time (a signal) into the frequencies that make it up
Original toplevel document
Fourier transform - Wikipediactions for the group of translations. Fourier transforms Continuous Fourier transform Fourier series Discrete-time Fourier transform Discrete Fourier transform Discrete Fourier transform over a ring Fourier analysis Related transforms <span>The Fourier transform (FT) decomposes a function of time (a signal) into the frequencies that make it up, in a way similar to how a musical chord can be expressed as the frequencies (or pitches) of its constituent notes. The Fourier transform of a function of time itself is a complex-value
Flashcard 1729631751436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function.
Original toplevel document
Characteristic function (probability theory) - Wikipediac around the origin; however characteristic functions may generally be complex-valued. In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. <span>If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There ar
Flashcard 1729633324300
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itn probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution.
Original toplevel document
Characteristic function (probability theory) - Wikipediaaracteristic function of a uniform U(–1,1) random variable. This function is real-valued because it corresponds to a random variable that is symmetric around the origin; however characteristic functions may generally be complex-valued. I<span>n probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides the basis of
Flashcard 1729634897164
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itViewed as a machine-learning algorithm, a Gaussian process uses lazy learning and a measure of the similarity between points (the kernel function) to predict the value for an unseen point from training data.
Original toplevel document
Gaussian process - Wikipediaf them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. <span>Viewed as a machine-learning algorithm, a Gaussian process uses lazy learning and a measure of the similarity between points (the kernel function) to predict the value for an unseen point from training data. The prediction is not just an estimate for that point, but also has uncertainty information—it is a one-dimensional Gaussian distribution (which is the marginal distribution at that poi
Flashcard 1729636470028
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itViewed as a machine-learning algorithm, a Gaussian process uses lazy learning and a measure of the similarity between points (the kernel function) to predict the value for an unseen point from training data.
Original toplevel document
Gaussian process - Wikipediaf them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. <span>Viewed as a machine-learning algorithm, a Gaussian process uses lazy learning and a measure of the similarity between points (the kernel function) to predict the value for an unseen point from training data. The prediction is not just an estimate for that point, but also has uncertainty information—it is a one-dimensional Gaussian distribution (which is the marginal distribution at that poi
Flashcard 1729641712908
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe eigendecomposition can be derived from the fundamental property of eigenvectors: and thus which yields .
Original toplevel document
Eigendecomposition of a matrix - Wikipedia, {\displaystyle v_{i}\,\,(i=1,\dots ,N),} can also be used as the columns of Q. That can be understood by noting that the magnitude of the eigenvectors in Q gets canceled in the decomposition by the presence of Q −1 . <span>The decomposition can be derived from the fundamental property of eigenvectors: A v = λ v {\displaystyle \mathbf {A} \mathbf {v} =\lambda \mathbf {v} } and thus A Q = Q Λ {\displaystyle \mathbf {A} \mathbf {Q} =\mathbf {Q} \mathbf {\Lambda } } which yields A = Q Λ Q − 1 {\displaystyle \mathbf {A} =\mathbf {Q} \mathbf {\Lambda } \mathbf {Q} ^{-1}} . Example[edit source] Taking a 2 × 2 real matrix A = [
Flashcard 1729643285772
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe eigendecomposition can be derived from the fundamental property of eigenvectors: and thus which yields .
Original toplevel document
Eigendecomposition of a matrix - Wikipedia, {\displaystyle v_{i}\,\,(i=1,\dots ,N),} can also be used as the columns of Q. That can be understood by noting that the magnitude of the eigenvectors in Q gets canceled in the decomposition by the presence of Q −1 . <span>The decomposition can be derived from the fundamental property of eigenvectors: A v = λ v {\displaystyle \mathbf {A} \mathbf {v} =\lambda \mathbf {v} } and thus A Q = Q Λ {\displaystyle \mathbf {A} \mathbf {Q} =\mathbf {Q} \mathbf {\Lambda } } which yields A = Q Λ Q − 1 {\displaystyle \mathbf {A} =\mathbf {Q} \mathbf {\Lambda } \mathbf {Q} ^{-1}} . Example[edit source] Taking a 2 × 2 real matrix A = [
Flashcard 1729646955788
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonal
Original toplevel document
Eigendecomposition of a matrix - Wikipedia| ocultar ahora Eigendecomposition of a matrix From Wikipedia, the free encyclopedia (Redirected from Eigendecomposition) Jump to: navigation, search <span>In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. Contents [hide] 1 Fundamental theory of matrix eigenvectors and eigenvalues 2 Eigendecomposition of a matrix 2.1 Example 2.2 Matrix inverse via eigendecomposition 2.2.1 Pr
Flashcard 1729648528652
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in
Original toplevel document
Eigendecomposition of a matrix - Wikipedia| ocultar ahora Eigendecomposition of a matrix From Wikipedia, the free encyclopedia (Redirected from Eigendecomposition) Jump to: navigation, search <span>In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. Contents [hide] 1 Fundamental theory of matrix eigenvectors and eigenvalues 2 Eigendecomposition of a matrix 2.1 Example 2.2 Matrix inverse via eigendecomposition 2.2.1 Pr
Flashcard 1729650101516
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way.
Original toplevel document
Eigendecomposition of a matrix - Wikipedia| ocultar ahora Eigendecomposition of a matrix From Wikipedia, the free encyclopedia (Redirected from Eigendecomposition) Jump to: navigation, search <span>In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. Contents [hide] 1 Fundamental theory of matrix eigenvectors and eigenvalues 2 Eigendecomposition of a matrix 2.1 Example 2.2 Matrix inverse via eigendecomposition 2.2.1 Pr
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itIn geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, tho
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
Flashcard 1729653247244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes.
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itmap [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. <span>An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. <span><body><html>
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
Flashcard 1729656392972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
Flashcard 1729657965836
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
Flashcard 1729659538700
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.
Original toplevel document
Affine transformation - Wikipedias related to each other leaf by an affine transformation. For instance, the red leaf can be transformed into both the small dark blue leaf and the large light blue leaf by a combination of reflection, rotation, scaling, and translation. <span>In geometry, an affine transformation, affine map [1] or an affinity (from the Latin, affinis, "connected with") is a function between affine spaces which preserves points, straight lines and planes. Also, sets of parallel lines remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. Examples of affine transformations include translation, scaling, homothety, similarity transformation, reflection, rotation, shear mapping, and compositions of them in any combination
Flashcard 1729661111564
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
Original toplevel document
Ellipsoid - Wikipedia= 1 : {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:} sphere (top, a=b=c=4), spheroid (bottom left, a=b=5, c=3), tri-axial ellipsoid (bottom right, a=4.5, b=6, c=3) <span>An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface, that is a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is char
Flashcard 1729662684428
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itAn ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
Original toplevel document
Ellipsoid - Wikipedia= 1 : {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1:} sphere (top, a=b=c=4), spheroid (bottom left, a=b=5, c=3), tri-axial ellipsoid (bottom right, a=4.5, b=6, c=3) <span>An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface, that is a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is char
Flashcard 1729664257292
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe distribution N(μ, Σ) is in effect N(0, I) scaled by Λ 1/2 , rotated by U and translated by μ.
Original toplevel document
Multivariate normal distribution - Wikipedia{\mu }}+\mathbf {U} {\mathcal {N}}(0,{\boldsymbol {\Lambda }}).} Moreover, U can be chosen to be a rotation matrix, as inverting an axis does not have any effect on N(0, Λ), but inverting a column changes the sign of U's determinant. <span>The distribution N(μ, Σ) is in effect N(0, I) scaled by Λ 1/2 , rotated by U and translated by μ. Conversely, any choice of μ, full rank matrix U, and positive diagonal entries Λ i yields a non-singular multivariate normal distribution. If any Λ i is zero and U is square, the re
Flashcard 1729666616588
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix Σ. The squared relative lengths of the principal axes are given by the corresponding eigenvalues.
Original toplevel document
Multivariate normal distribution - Wikipediaurs of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean. [17] Hence the multivariate normal distribution is an example of the class of elliptical distributions. <span>The directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix Σ. The squared relative lengths of the principal axes are given by the corresponding eigenvalues. If Σ = UΛU T = UΛ 1/2 (UΛ 1/2 ) T is an eigendecomposition where the columns of U are unit eigenvectors and Λ is a diagonal matrix of the eigenvalues, then we have
Flashcard 1729668189452
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix Σ. The squared relative lengths of the principal axes are given by the corresponding eigenvalues.
Original toplevel document
Multivariate normal distribution - Wikipediaurs of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean. [17] Hence the multivariate normal distribution is an example of the class of elliptical distributions. <span>The directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix Σ. The squared relative lengths of the principal axes are given by the corresponding eigenvalues. If Σ = UΛU T = UΛ 1/2 (UΛ 1/2 ) T is an eigendecomposition where the columns of U are unit eigenvectors and Λ is a diagonal matrix of the eigenvalues, then we have
Flashcard 1729669762316
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe equidensity contours of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean.
Original toplevel document
Multivariate normal distribution - Wikipediaimplies that the variance of the dot product must be positive. An affine transformation of X such as 2X is not the same as the sum of two independent realisations of X. Geometric interpretation[edit source] See also: Confidence region <span>The equidensity contours of a non-singular multivariate normal distribution are ellipsoids (i.e. linear transformations of hyperspheres) centered at the mean. [17] Hence the multivariate normal distribution is an example of the class of elliptical distributions. The directions of the principal axes of the ellipsoids are given by the eigenvec
Flashcard 1729672908044
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIf Y = c + BX is an affine transformation of where c is an vector of constants and B is a constant matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB T . Corollaries: sums of Gaussian are Gaussian, marginals of Gaussian are Gaussian.
Original toplevel document
Multivariate normal distribution - Wikipedia{\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}} . Affine transformation[edit source] <span>If Y = c + BX is an affine transformation of X ∼ N ( μ , Σ ) , {\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}),} where c is an M × 1 {\displaystyle M\times 1} vector of constants and B is a constant M × N {\displaystyle M\times N} matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB T i.e., Y ∼ N ( c + B μ , B Σ B T ) {\displaystyle \mathbf {Y} \sim {\mathcal {N}}\left(\mathbf {c} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} {\boldsymbol {\Sigma }}\mathbf {B} ^{\rm {T}}\right)} . In particular, any subset of the X i has a marginal distribution that is also multivariate normal. To see this, consider the following example: to extract the subset (X 1 , X 2 , X 4 )
Flashcard 1729674480908
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open it><head> If Y = c + BX is an affine transformation of where c is an vector of constants and B is a constant matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB T . Corollaries: sums of Gaussian are Gaussian, marginals of Gaussian are Gaussian. <html>
Original toplevel document
Multivariate normal distribution - Wikipedia{\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}} . Affine transformation[edit source] <span>If Y = c + BX is an affine transformation of X ∼ N ( μ , Σ ) , {\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }}),} where c is an M × 1 {\displaystyle M\times 1} vector of constants and B is a constant M × N {\displaystyle M\times N} matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB T i.e., Y ∼ N ( c + B μ , B Σ B T ) {\displaystyle \mathbf {Y} \sim {\mathcal {N}}\left(\mathbf {c} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} {\boldsymbol {\Sigma }}\mathbf {B} ^{\rm {T}}\right)} . In particular, any subset of the X i has a marginal distribution that is also multivariate normal. To see this, consider the following example: to extract the subset (X 1 , X 2 , X 4 )
Flashcard 1729676053772
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTo obtain the marginal distribution over a subset of multivariate normal random variables, one only needs to drop the irrelevant variables (the variables that one wants to marginalize out) from the mean vector and the covariance matrix. The proof for this follows from the definitions of multivariate normal distributions an
Original toplevel document
Multivariate normal distribution - Wikipedia) {\displaystyle \operatorname {E} (X_{1}\mid X_{2}##BAD TAG##\rho E(X_{2}\mid X_{2}##BAD TAG##} and then using the properties of the expectation of a truncated normal distribution. Marginal distributions[edit source] <span>To obtain the marginal distribution over a subset of multivariate normal random variables, one only needs to drop the irrelevant variables (the variables that one wants to marginalize out) from the mean vector and the covariance matrix. The proof for this follows from the definitions of multivariate normal distributions and linear algebra. [16] Example Let X = [X 1 , X 2 , X 3 ] be multivariate normal random variables with mean vector μ = [μ 1 , μ 2 , μ 3 ] and covariance matrix Σ (standard parametrization for multivariate
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itConditional distributions If N-dimensional x is partitioned as follows and accordingly μ and Σ are partitioned as follows then the distribution of x 1 conditional on x 2 = a is multivariate normal (x 1 | x 2 = a) ~ N( μ , Σ ) where and covariance matrix This matrix is the Schur complement of Σ 22 in Σ. This means that to calculate the conditional covariance matrix, one inverts the overall covariance matrix, drops t
Original toplevel document
Multivariate normal distribution - Wikipediay two or more of its components that are pairwise independent are independent. But, as pointed out just above, it is not true that two random variables that are (separately, marginally) normally distributed and uncorrelated are independent. <span>Conditional distributions[edit source] If N-dimensional x is partitioned as follows x = [ x 1 x 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle \mathbf {x} ={\begin{bmatrix}\mathbf {x} _{1}\\\mathbf {x} _{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} and accordingly μ and Σ are partitioned as follows μ = [ μ 1 μ 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle {\boldsymbol {\mu }}={\begin{bmatrix}{\boldsymbol {\mu }}_{1}\\{\boldsymbol {\mu }}_{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] with sizes [ q × q q × ( N − q ) ( N − q ) × q ( N − q ) × ( N − q ) ] {\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{12}\\{\boldsymbol {\Sigma }}_{21}&{\boldsymbol {\Sigma }}_{22}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times q&q\times (N-q)\\(N-q)\times q&(N-q)\times (N-q)\end{bmatrix}}} then the distribution of x 1 conditional on x 2 = a is multivariate normal (x 1 | x 2 = a) ~ N(μ, Σ) where μ ¯ = μ 1 + Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\bar {\boldsymbol {\mu }}}={\boldsymbol {\mu }}_{1}+{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} and covariance matrix Σ ¯ = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 . {\displaystyle {\overline {\boldsymbol {\Sigma }}}={\boldsymbol {\Sigma }}_{11}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}{\boldsymbol {\Sigma }}_{21}.} [13] This matrix is the Schur complement of Σ 22 in Σ. This means that to calculate the conditional covariance matrix, one inverts the overall covariance matrix, drops the rows and columns corresponding to the variables being conditioned upon, and then inverts back to get the conditional covariance matrix. Here Σ 22 − 1 {\displaystyle {\boldsymbol {\Sigma }}_{22}^{-1}} is the generalized inverse of Σ 22 {\displaystyle {\boldsymbol {\Sigma }}_{22}} . Note that knowing that x 2 = a alters the variance, though the new variance does not depend on the specific value of a; perhaps more surprisingly, the mean is shifted by Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} ; compare this with the situation of not knowing the value of a, in which case x 1 would have distribution N q ( μ 1 , Σ 11 ) {\displaystyle {\mathcal {N}}_{q}\left({\boldsymbol {\mu }}_{1},{\boldsymbol {\Sigma }}_{11}\right)} . An interesting fact derived in order to prove this result, is that the random vectors x 2 {\displaystyle \mathbf {x} _{2}} and y 1 = x 1 − Σ 12 Σ 22 − 1 x 2 {\displaystyle \mathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}} are independent. The matrix Σ 12 Σ 22 −1 is known as the matrix of regression coefficients. Bivariate case[edit source] In the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is [14]
Flashcard 1729680772364
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe distribution of x 1 conditional on x 2 = a is multivariate normal (x 1 | x 2 = a) ~ N( μ , Σ ) where and covariance matrix
Original toplevel document
Multivariate normal distribution - Wikipediay two or more of its components that are pairwise independent are independent. But, as pointed out just above, it is not true that two random variables that are (separately, marginally) normally distributed and uncorrelated are independent. <span>Conditional distributions[edit source] If N-dimensional x is partitioned as follows x = [ x 1 x 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle \mathbf {x} ={\begin{bmatrix}\mathbf {x} _{1}\\\mathbf {x} _{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} and accordingly μ and Σ are partitioned as follows μ = [ μ 1 μ 2 ] with sizes [ q × 1 ( N − q ) × 1 ] {\displaystyle {\boldsymbol {\mu }}={\begin{bmatrix}{\boldsymbol {\mu }}_{1}\\{\boldsymbol {\mu }}_{2}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times 1\\(N-q)\times 1\end{bmatrix}}} Σ = [ Σ 11 Σ 12 Σ 21 Σ 22 ] with sizes [ q × q q × ( N − q ) ( N − q ) × q ( N − q ) × ( N − q ) ] {\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{12}\\{\boldsymbol {\Sigma }}_{21}&{\boldsymbol {\Sigma }}_{22}\end{bmatrix}}{\text{ with sizes }}{\begin{bmatrix}q\times q&q\times (N-q)\\(N-q)\times q&(N-q)\times (N-q)\end{bmatrix}}} then the distribution of x 1 conditional on x 2 = a is multivariate normal (x 1 | x 2 = a) ~ N(μ, Σ) where μ ¯ = μ 1 + Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\bar {\boldsymbol {\mu }}}={\boldsymbol {\mu }}_{1}+{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} and covariance matrix Σ ¯ = Σ 11 − Σ 12 Σ 22 − 1 Σ 21 . {\displaystyle {\overline {\boldsymbol {\Sigma }}}={\boldsymbol {\Sigma }}_{11}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}{\boldsymbol {\Sigma }}_{21}.} [13] This matrix is the Schur complement of Σ 22 in Σ. This means that to calculate the conditional covariance matrix, one inverts the overall covariance matrix, drops the rows and columns corresponding to the variables being conditioned upon, and then inverts back to get the conditional covariance matrix. Here Σ 22 − 1 {\displaystyle {\boldsymbol {\Sigma }}_{22}^{-1}} is the generalized inverse of Σ 22 {\displaystyle {\boldsymbol {\Sigma }}_{22}} . Note that knowing that x 2 = a alters the variance, though the new variance does not depend on the specific value of a; perhaps more surprisingly, the mean is shifted by Σ 12 Σ 22 − 1 ( a − μ 2 ) {\displaystyle {\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\left(\mathbf {a} -{\boldsymbol {\mu }}_{2}\right)} ; compare this with the situation of not knowing the value of a, in which case x 1 would have distribution N q ( μ 1 , Σ 11 ) {\displaystyle {\mathcal {N}}_{q}\left({\boldsymbol {\mu }}_{1},{\boldsymbol {\Sigma }}_{11}\right)} . An interesting fact derived in order to prove this result, is that the random vectors x 2 {\displaystyle \mathbf {x} _{2}} and y 1 = x 1 − Σ 12 Σ 22 − 1 x 2 {\displaystyle \mathbf {y} _{1}=\mathbf {x} _{1}-{\boldsymbol {\Sigma }}_{12}{\boldsymbol {\Sigma }}_{22}^{-1}\mathbf {x} _{2}} are independent. The matrix Σ 12 Σ 22 −1 is known as the matrix of regression coefficients. Bivariate case[edit source] In the bivariate case where x is partitioned into X 1 and X 2 , the conditional distribution of X 1 given X 2 is [14]
Flashcard 1729683393804
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe pseudoinverse is defined and unique for all matrices whose entries are real or complex numbers. It can be computed using the singular value decomposition.
Original toplevel document
Moore–Penrose inverse - Wikipediation (see below under § Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. The pseudoinverse facilitates the statement and proof of results in linear algebra. <span>The pseudoinverse is defined and unique for all matrices whose entries are real or complex numbers. It can be computed using the singular value decomposition. Contents [hide] 1 Notation 2 Definition 3 Properties 3.1 Existence and uniqueness 3.2 Basic properties 3.2.1 Identities 3.3 Reduction to Hermitian case 3.4 Products 3.5
Flashcard 1729684966668
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA common use of the pseudoinverse is to compute a 'best fit' (least squares) solution to a system of linear equations that lacks a unique solution
Original toplevel document
Moore–Penrose inverse - Wikipediategral operators in 1903. When referring to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose inverse. The term generalized inverse is sometimes used as a synonym for pseudoinverse. <span>A common use of the pseudoinverse is to compute a 'best fit' (least squares) solution to a system of linear equations that lacks a unique solution (see below under § Applications). Another use is to find the minimum (Euclidean) norm solution to a system of linear equations with multiple solutions. The pseudoinverse facilitates the
Flashcard 1729687325964
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itFormally, given a matrix and a matrix , A is a generalized inverse of if it satisfies the condition : .
Original toplevel document
Generalized inverse - Wikipedianverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A {\displaystyle A} . <span>Formally, given a matrix A ∈ R n × m {\displaystyle A\in \mathbb {R} ^{n\times m}} and a matrix A g ∈ R m × n {\displaystyle A^{\mathrm {g} }\in \mathbb {R} ^{m\times n}} , A g {\displaystyle A^{\mathrm {g} }} is a generalized inverse of A {\displaystyle A} if it satisfies the condition A A g A = A {\displaystyle AA^{\mathrm {g} }A=A} . [1] [2] [3] The purpose of constructing a generalized inverse of a matrix is to obtain a matrix that can serve as an inverse in some sense for a wider class of matrices than invertibl
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itIn mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup.
Original toplevel document
Generalized inverse - Wikipediaree encyclopedia Jump to: navigation, search "Pseudoinverse" redirects here. For the Moore–Penrose inverse, sometimes referred to as "the pseudoinverse", see Moore–Penrose inverse. <span>In mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A {\displaystyle A} . Formally, given a matrix A ∈
Flashcard 1729691258124
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them.
Original toplevel document
Generalized inverse - Wikipediaree encyclopedia Jump to: navigation, search "Pseudoinverse" redirects here. For the Moore–Penrose inverse, sometimes referred to as "the pseudoinverse", see Moore–Penrose inverse. <span>In mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix A {\displaystyle A} . Formally, given a matrix A ∈
Flashcard 1729692830988
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn the bivariate case the expression for the mutual information is:
Original toplevel document
Multivariate normal distribution - Wikipedialdsymbol {\rho }}_{0}} is the correlation matrix constructed from Σ 0 {\displaystyle {\boldsymbol {\Sigma }}_{0}} . <span>In the bivariate case the expression for the mutual information is: I ( x ; y ) = − 1 2 ln ( 1 − ρ 2 ) . {\displaystyle I(x;y)=-{1 \over 2}\ln(1-\rho ^{2}).} Cumulative distribution function[edit source] The notion of cumulative distribution function (cdf) in dimension 1 can be extended in two ways to the multidimensional case, based
Flashcard 1729696763148
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe mutual information of a distribution is a special case of the Kullback–Leibler divergence in which is the full multivariate distribution and is the product of the 1-dimensional marginal distributions
Original toplevel document
Multivariate normal distribution - Wikipediaal {CN}}_{0}\|{\mathcal {CN}}_{1})=\operatorname {tr} \left({\boldsymbol {\Sigma }}_{1}^{-1}{\boldsymbol {\Sigma }}_{0}\right)-k+\ln {|{\boldsymbol {\Sigma }}_{1}| \over |{\boldsymbol {\Sigma }}_{0}|}.} Mutual information[edit source] <span>The mutual information of a distribution is a special case of the Kullback–Leibler divergence in which P {\displaystyle P} is the full multivariate distribution and Q {\displaystyle Q} is the product of the 1-dimensional marginal distributions. In the notation of the Kullback–Leibler divergence section of this article, Σ 1
Flashcard 1729699122444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value
Original toplevel document
Multivariate normal distribution - Wikipediae definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. <span>The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Contents [hide] 1 Notation and parametrization 2 Definition 3 Properties 3.1 Density function 3.1.1 Non-degenerate case 3.1.2 Degenerate case 3.2 Higher moments 3.3 Lik
Flashcard 1729700695308
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itOne definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution.
Original toplevel document
Multivariate normal distribution - Wikipediaa }}\mathbf {t} {\Big )}} In probability theory and statistics, the multivariate normal distribution or multivariate Gaussian distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. <span>One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly)
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itThe negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed as a gamma distribution with shape = r and scale θ = p/(1 − p)
Original toplevel document
Negative binomial distribution - Wikipedia) . {\displaystyle \operatorname {Poisson} (\lambda )=\lim _{r\to \infty }\operatorname {NB} \left(r,{\frac {\lambda }{\lambda +r}}\right).} Gamma–Poisson mixture[edit source] <span>The negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed as a gamma distribution with shape = r and scale θ = p/(1 − p) or correspondingly rate β = (1 − p)/p. To display the intuition behind this statement, consider two independent Poisson processes, “Success” and “Failure”, with intensities p and 1 − p. Together, the Success and Failure pr
Flashcard 1729703841036
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution.
Original toplevel document
Negative binomial distribution - Wikipedia) . {\displaystyle \operatorname {Poisson} (\lambda )=\lim _{r\to \infty }\operatorname {NB} \left(r,{\frac {\lambda }{\lambda +r}}\right).} Gamma–Poisson mixture[edit source] <span>The negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed as a gamma distribution with shape = r and scale θ = p/(1 − p) or correspondingly rate β = (1 − p)/p. To display the intuition behind this statement, consider two independent Poisson processes, “Success” and “Failure”, with intensities p and 1 − p. Together, the Success and Failure pr
Flashcard 1729705413900
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. </spa
Original toplevel document
Negative binomial distribution - Wikipedia) . {\displaystyle \operatorname {Poisson} (\lambda )=\lim _{r\to \infty }\operatorname {NB} \left(r,{\frac {\lambda }{\lambda +r}}\right).} Gamma–Poisson mixture[edit source] <span>The negative binomial distribution also arises as a continuous mixture of Poisson distributions (i.e. a compound probability distribution) where the mixing distribution of the Poisson rate is a gamma distribution. That is, we can view the negative binomial as a Poisson(λ) distribution, where λ is itself a random variable, distributed as a gamma distribution with shape = r and scale θ = p/(1 − p) or correspondingly rate β = (1 − p)/p. To display the intuition behind this statement, consider two independent Poisson processes, “Success” and “Failure”, with intensities p and 1 − p. Together, the Success and Failure pr
Flashcard 1729706986764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of fai
Original toplevel document
Negative binomial distribution - Wikipedia) 2 ( p ) {\displaystyle {\frac {r}{(1-p)^{2}(p)}}} <span>In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures (denoted r) occurs. For example, if we define a 1 as failure, all non-1s as successes, and we throw a dice repeatedly until the third time 1 appears (r = three failures), then the probability distribution
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Singular-value decomposition - Wikipedia
nto three simple transformations: an initial rotation V ∗ , a scaling Σ along the coordinate axes, and a final rotation U. The lengths σ 1 and σ 2 of the semi-axes of the ellipse are the singular values of M, namely Σ 1,1 and Σ 2,2 . <span>In linear algebra, the singular-value decomposition (SVD) is a factorization of a real or complex matrix. It is the generalization of the eigendecomposition of a positive semidefinite normal matrix (for example, a symmetric matrix with positive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. Formally, the singular-value decomposition of an m × n {\d
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Singular-value decomposition - Wikipedia
ositive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. <span>Formally, the singular-value decomposition of an m × n {\displaystyle m\times n} real or complex matrix M {\displaystyle \mathbf {M} } is a factorization of the form U Σ V ∗ {\displaystyle \mathbf {U\Sigma V^{*}} } , where U {\displaystyle \mathbf {U} } is an m × m {\displaystyle m\times m} real or complex unitary matrix, Σ {\displaystyle \mathbf {\Sigma } } is a m × n {\displaystyle m\times n} rectangular diagonal matrix with non-negative real numbers on the diagonal, and V {\displaystyle \mathbf {V} } is an n × n {\displaystyle n\times n} real or complex unitary matrix. The diagonal entries σ i {\displaystyle \sigma _{i}} of
Flashcard 1729714326796
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn linear algebra, the singular-value decomposition (SVD) generalises the eigendecomposition of a positive semidefinite normal matrix (for example, a symmetric matrix with positive eigenvalues) to any matrix via an extension of the polar deco
Original toplevel document
Singular-value decomposition - Wikipedianto three simple transformations: an initial rotation V ∗ , a scaling Σ along the coordinate axes, and a final rotation U. The lengths σ 1 and σ 2 of the semi-axes of the ellipse are the singular values of M, namely Σ 1,1 and Σ 2,2 . <span>In linear algebra, the singular-value decomposition (SVD) is a factorization of a real or complex matrix. It is the generalization of the eigendecomposition of a positive semidefinite normal matrix (for example, a symmetric matrix with positive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. Formally, the singular-value decomposition of an m × n {\d
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itFormally, the singular-value decomposition of an real or complex matrix is a factorization of the form , where is an real or complex unitary matrix, is a rectangular diagonal matrix with non-negative real numbers on the diagonal, and is an real or complex unitary matrix.
Original toplevel document
Singular-value decomposition - Wikipediaositive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. <span>Formally, the singular-value decomposition of an m × n {\displaystyle m\times n} real or complex matrix M {\displaystyle \mathbf {M} } is a factorization of the form U Σ V ∗ {\displaystyle \mathbf {U\Sigma V^{*}} } , where U {\displaystyle \mathbf {U} } is an m × m {\displaystyle m\times m} real or complex unitary matrix, Σ {\displaystyle \mathbf {\Sigma } } is a m × n {\displaystyle m\times n} rectangular diagonal matrix with non-negative real numbers on the diagonal, and V {\displaystyle \mathbf {V} } is an n × n {\displaystyle n\times n} real or complex unitary matrix. The diagonal entries σ i {\displaystyle \sigma _{i}} of
Flashcard 1729718258956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itFormally, the singular-value decomposition of an real or complex matrix is a factorization of the form
Original toplevel document
Singular-value decomposition - Wikipediaositive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. <span>Formally, the singular-value decomposition of an m × n {\displaystyle m\times n} real or complex matrix M {\displaystyle \mathbf {M} } is a factorization of the form U Σ V ∗ {\displaystyle \mathbf {U\Sigma V^{*}} } , where U {\displaystyle \mathbf {U} } is an m × m {\displaystyle m\times m} real or complex unitary matrix, Σ {\displaystyle \mathbf {\Sigma } } is a m × n {\displaystyle m\times n} rectangular diagonal matrix with non-negative real numbers on the diagonal, and V {\displaystyle \mathbf {V} } is an n × n {\displaystyle n\times n} real or complex unitary matrix. The diagonal entries σ i {\displaystyle \sigma _{i}} of
Flashcard 1729720618252
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itFormally, the singular-value decomposition of an real or complex matrix is a factorization of the form , where is an real or complex unitary matrix, is a rectangular diagonal matrix with non-negative real numbers on the diagonal, and is an real or complex unitary matrix.
Original toplevel document
Singular-value decomposition - Wikipediaositive eigenvalues) to any m × n {\displaystyle m\times n} matrix via an extension of the polar decomposition. It has many useful applications in signal processing and statistics. <span>Formally, the singular-value decomposition of an m × n {\displaystyle m\times n} real or complex matrix M {\displaystyle \mathbf {M} } is a factorization of the form U Σ V ∗ {\displaystyle \mathbf {U\Sigma V^{*}} } , where U {\displaystyle \mathbf {U} } is an m × m {\displaystyle m\times m} real or complex unitary matrix, Σ {\displaystyle \mathbf {\Sigma } } is a m × n {\displaystyle m\times n} rectangular diagonal matrix with non-negative real numbers on the diagonal, and V {\displaystyle \mathbf {V} } is an n × n {\displaystyle n\times n} real or complex unitary matrix. The diagonal entries σ i {\displaystyle \sigma _{i}} of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Object Oriented Programming – Quantitative Economics
ramming, and nicely supported in Python OOP has become an important concept in modern software engineering because It can help facilitate clean, efficient code (if used well) The OOP design pattern fits well with many computing problems <span>OOP is about producing well organized code — an important determinant of productivity Moreover, OOP is a part of Python, and to progress further it’s necessary to understand the basics About OOP¶ OOP is supported in many languages: JAVA and Ruby are relativel
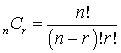
 is the full multivariate distribution and
is the full multivariate distribution and  is the product of the 1-dimensional marginal distributions
is the product of the 1-dimensional marginal distributions

 and a matrix
and a matrix  , A
, A  is a generalized inverse of
is a generalized inverse of  if it satisfies the condition :
if it satisfies the condition :  .
.
 , a pseudoinverse of
, a pseudoinverse of  satisfying all of the following four criteria:
satisfying all of the following four criteria: ( AA+ need not be the general identity matrix, but it maps all column vectors of A to themselves);
( AA+ need not be the general identity matrix, but it maps all column vectors of A to themselves); ( A+ is a
( A+ is a  ( AA+ is
( AA+ is  ( A+A is also Hermitian).
( A+A is also Hermitian). exists for any matrix
exists for any matrix  is invertible),
is invertible),  ...
...





 is the
is the  .
. ; compare this with the situation of not knowing the value of a, in which case x1 would have distribution
; compare this with the situation of not knowing the value of a, in which case x1 would have distribution  .
. and
and  are independent.
are independent. where c is an
where c is an  vector of constants and B is a constant
vector of constants and B is a constant  matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣBT .
matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣBT . and thus
and thus  which yields
which yields  .
.

 is the
is the  correspond to customers and the columns correspond to dishes in an infinitely long buffet.
correspond to customers and the columns correspond to dishes in an infinitely long buffet.

 matrix via an extension of the
matrix via an extension of the  is a factorization of the form
is a factorization of the form  , where
, where  is an
is an  real or complex
real or complex  is a
is a  is an
is an  real or complex unitary matrix.
real or complex unitary matrix.