Edited, memorised or added to reading queue
on 06-Jul-2014 (Sun)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Article 149623329
calculating asset swap spread (par-par)
#asset-swap #finance
Asset swap (type: par-par - same structure as market but at different price, i.e. PV. "market" has 0 PV) is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond.
Flashcard 149623338
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
calculating asset swap spread
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond
Flashcard 149623345
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
calculating asset swap spread
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond.
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond.
Flashcard 149623352
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
calculating asset swap spread
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond.
Asset swap is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap side that matches the maturity of the bond.
Flashcard 149623398
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
calculating asset swap spread (par-par)
Asset swap (type: market - same structure as par-par but at different price) is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap
Asset swap (type: market - same structure as par-par but at different price) is a difference between bond quoted price and implied strip price of the same bond (implied price of cashflows against a specific yield curve), quoted as the spread on the floating swap
Flashcard 149623553
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn the market asset swap, the net upfront payment is zero. Instead the notional on the Libor side equals the price of the bond and there is an exchange of notionals at maturity.
Original toplevel document
Asset swap - Wikipedia, the free encyclopediaeen floating side coupons, the floating payment received is half of the Libor plus asset swap spread. This feature prevents the calculated asset swap spread from jumping as we move forward in time through coupon dates. Market Asset Swap[edit] <span>In the market asset swap, the net upfront payment is zero. Instead the notional on the Libor side equals the price of the bond and there is an exchange of notionals at maturity. See also[edit] Government debtInterestSwap (finance) References[edit] ^ "Asset Swap - Investopedia". Investopedia. Archived from the original on 12 April 2009. Retrieved 2009-0
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
d to add to the curve you are discounting with in order to generate a price that matches the market price. Conventionally, the zero rates are determined from the Treasury curve, with semi-annual compounding. The Problem with YTM spreads[edit] <span>Coupon Paying bonds are essentially portfolios of Zero Coupon Bond components and the Yield to Maturity of such instruments can be thought of as being a complex blend of the component Zero Coupon bond yields. It therefore can be observed that, for example, in a positively sloped Yield Curve environment and comparing two bonds with the same cash flow dates and maturity, a higher coupon bond will offer a lower YTM than a low coupon bond. (The low coupon bond has cash flows more heavily influenced by a proportionally greater long term component). Thus two fairly and correctly priced corporate bonds from the same borrower and having the same cash flow dates and maturity may well have significantly different Yields to Maturity. It
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity (economics) - Wikipedia, the free encyclopedia
nclear to readers. Please help us clarify the article; suggestions may be found on the talk page. (December 2010) In economics, elasticity is the measurement of how responsive an economic variable is to a change in another. For example: "<span>If I lower the price of my product, how much more will I sell?""If I raise the price of one good, how will that affect sales of this other good?""If we learn that a resource is becoming scarce, will people scramble to acquire it
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itThis theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result, the supply and demand in the markets for short-term and long-term instruments is determined largely independently. Prospective investors decide in advance whether they need
Original toplevel document
Yield curve - Wikipedia, the free encyclopediabecause of the risk premium added by the risk of default from holding a security over the long term. The market expectations hypothesis is combined with the liquidity premium theory: Where is the risk premium associated with an year bond. <span>Market segmentation theory[edit] This theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result, the supply and demand in the markets for short-term and long-term instruments is determined largely independently. Prospective investors decide in advance whether they need short-term or long-term instruments. If investors prefer their portfolio to be liquid, they will prefer short-term instruments to long-term instruments. Therefore, the market for short-term instruments will receive a higher demand. Higher demand for the instrument implies higher prices and lower yield. This explains the stylized fact that short-term yields are usually lower than long-term yields. This theory explains the predominance of the normal yield curve shape. However, because the supply and demand of the two markets are independent, this theory fails to explain the observed fact that yields tend to move together (i.e., upward and downward shifts in the curve). Preferred habitat theory[edit] The preferred habitat theory is another guide of the liquidity premium theory, and states that in addition to interest rate expectations, investors have di
Flashcard 149624416
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itIn Market Segmentation Theory of yield curve shape, financial instruments of different terms are not substitutable.
Original toplevel document
Yield curve - Wikipedia, the free encyclopediabecause of the risk premium added by the risk of default from holding a security over the long term. The market expectations hypothesis is combined with the liquidity premium theory: Where is the risk premium associated with an year bond. <span>Market segmentation theory[edit] This theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result, the supply and demand in the markets for short-term and long-term instruments is determined largely independently. Prospective investors decide in advance whether they need short-term or long-term instruments. If investors prefer their portfolio to be liquid, they will prefer short-term instruments to long-term instruments. Therefore, the market for short-term instruments will receive a higher demand. Higher demand for the instrument implies higher prices and lower yield. This explains the stylized fact that short-term yields are usually lower than long-term yields. This theory explains the predominance of the normal yield curve shape. However, because the supply and demand of the two markets are independent, this theory fails to explain the observed fact that yields tend to move together (i.e., upward and downward shifts in the curve). Preferred habitat theory[edit] The preferred habitat theory is another guide of the liquidity premium theory, and states that in addition to interest rate expectations, investors have di
Flashcard 149624483
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTED is an acronym formed from T-Bill and ED, the ticker symbol for the Eurodollar futures contract.
Original toplevel document
TED spread - Wikipedia, the free encyclopediay of the TED spread TED spread (in red) and components during the Financial crisis of 2007–08 The TED spread is the difference between the interest rates on interbank loans and on short-term U.S. government debt ("T-bills"). <span>TED is an acronym formed from T-Bill and ED, the ticker symbol for the Eurodollar futures contract. Initially, the TED spread was the difference between the interest rates for three-month U.S. Treasuries contracts and the three-month Eurodollars contract as represented by the London In
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itThe Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve
Original toplevel document
I-spread - Wikipedia, the free encyclopediaenwiki:resourceloader:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ I-spread From Wikipedia, the free encyclopedia Jump to: navigation, search <span>The Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve.[1] See also[edit] Option-adjusted spreadZ-spread References[edit] ^ Credit Spreads Explained vte Bond market BondDebentureFixed income Types of bonds by issuer Agency bondCor
Flashcard 149624497
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itInterpolated Spread or I-spread or ISPRD
Original toplevel document
I-spread - Wikipedia, the free encyclopediaenwiki:resourceloader:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ I-spread From Wikipedia, the free encyclopedia Jump to: navigation, search <span>The Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve.[1] See also[edit] Option-adjusted spreadZ-spread References[edit] ^ Credit Spreads Explained vte Bond market BondDebentureFixed income Types of bonds by issuer Agency bondCor
Flashcard 149624508
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve
Original toplevel document
I-spread - Wikipedia, the free encyclopediaenwiki:resourceloader:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ I-spread From Wikipedia, the free encyclopedia Jump to: navigation, search <span>The Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve.[1] See also[edit] Option-adjusted spreadZ-spread References[edit] ^ Credit Spreads Explained vte Bond market BondDebentureFixed income Types of bonds by issuer Agency bondCor
Flashcard 149624515
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve
Original toplevel document
I-spread - Wikipedia, the free encyclopediaenwiki:resourceloader:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ I-spread From Wikipedia, the free encyclopedia Jump to: navigation, search <span>The Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve.[1] See also[edit] Option-adjusted spreadZ-spread References[edit] ^ Credit Spreads Explained vte Bond market BondDebentureFixed income Types of bonds by issuer Agency bondCor
Flashcard 149624525
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itonly the anticipation of falling interest rates will cause an inverted yield curve.
Original toplevel document
Yield curve - Wikipedia, the free encyclopediabond. The market's anticipation of falling interest rates causes such incidents. Negative liquidity premiums can also exist if long-term investors dominate the market, but the prevailing view is that a positive liquidity premium dominates, so <span>only the anticipation of falling interest rates will cause an inverted yield curve. Strongly inverted yield curves have historically preceded economic depressions. The shape of the yield curve is influenced by supply and demand: for instance, if there is a large demand
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itMain article: expectation hypothesis This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants' expectations of future interest rates. Using this, future rates, along with the assumption that arbitrage opportunities will be minimal in future markets, and that future rates are unbiased estimates of forthcoming spot rates
Original toplevel document
Yield curve - Wikipedia, the free encyclopediag in a credit bubble. Theory[edit] There are three main economic theories attempting to explain how yields vary with maturity. Two of the theories are extreme positions, while the third attempts to find a middle ground between the former two. <span>Market expectations (pure expectations) hypothesis[edit] Main article: expectation hypothesis This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants' expectations of future interest rates. Using this, future rates, along with the assumption that arbitrage opportunities will be minimal in future markets, and that future rates are unbiased estimates of forthcoming spot rates, is enough information to construct a complete expected yield curve. For example, if investors have an expectation of what 1-year interest rates will be next year, the 2-year interest rate can be calculated as the compounding of this year's interest rate by next year's interest rate. More generally, rates on a long-term instrument are equal to the geometric mean of the yield on a series of short-term instruments. This theory perfectly explains the observation that yields usually move together. However, it fails to explain the persistence in the shape of the yield curve. Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk Liquidity premium theory[edit] The Liquidity Premium Theory is an offshoot of the Pure Expectations Theory. The Liquidity Premium Theory asserts that long-term interest rates not only re
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
of the yield , not varying by term to payment. With the use of computers, both forms may be calculated but expression (3), assuming a constant yield, is more widely used because of the application to modified duration. Modified duration[edit] <span>In contrast to Macaulay duration, modified duration (sometimes abbreviated MD) is a price sensitivity measure, defined as the percentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out th
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
percentage derivative of price with respect to yield. Modified duration applies when a bond or other asset is considered as a function of yield. In this case one can measure the logarithmic derivative with respect to yield: It turns out that <span>when the yield is expressed continuously compounded, Macaulay duration and modified duration are equal. First, consider the case of continuously compounded yields. If we take the derivative of price or present value, expression (2), with respect to the continuously compounded yield we see
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
uously compounded. Then expression (2) becomes: To find modified duration, when we take the derivative of the value with respect to the periodically compounded yield we find [5] Rearranging (dividing both sides by -V) gives: which is the <span>well-known relationship between modified duration and Macaulay duration: where: indexes the cash flows, is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.), is the cash flow of the th payment from an asset, is the time in years until the th payment will be received (e.g. a two-year semi-annual would be represented by a index of 0.5, 1.0, 1.5, and 2.0), is the yield to maturity for an asset, periodically compounded is the present value of all cash payments from the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are clo
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
the asset. This gives the well-known relation between Macaulay duration and modified duration quoted above. It should be remembered that, even though Macaulay duration and modified duration are closely related, they are conceptually distinct. <span>Macaulay duration is a weighted average time until repayment (measured in units of time such as years) while modified duration is a price sensitivity measure when the price is treated as a function of yield, the percentage change in price with respect to yield. Units[edit] For modified du
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
t should be remembered that, even though Macaulay duration and modified duration are closely related, they are conceptually distinct. Macaulay duration is a weighted average time until repayment (measured in units of time such as years) while <span>modified duration is a price sensitivity measure when the price is treated as a function of yield, the percentage change in price with respect to yield. Units[edit] For modified duration the common units are the percent change in price per one percentage point change in yield per year (for example yield going from 8% per year (y = 0.08)
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
average time until repayment (measured in units of time such as years) while modified duration is a price sensitivity measure when the price is treated as a function of yield, the percentage change in price with respect to yield. Units[edit] <span>For modified duration the common units are the percent change in price per one percentage point change in yield per year (for example yield going from 8% per year (y = 0.08) to 9% per year (y = 0.09)). This will give modified duration close to the value of Macaulay duration (and the same when rates are continuously compounded). Formally, modified duration is a semi-elasticity, the percent change in price for a unit change in yield, rather than an elasticity, which is a percentage change in output for a percen
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Greeks (finance) - Wikipedia, the free encyclopedia
or4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open ittaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). <span>First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest.</spa
Original toplevel document
Greeks (finance) - Wikipedia, the free encyclopediaor4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
Flashcard 149624637
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSpot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega Theta Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are i
Original toplevel document
Greeks (finance) - Wikipedia, the free encyclopediaor4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
Flashcard 149624648
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSpot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega Theta Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blu
Original toplevel document
Greeks (finance) - Wikipedia, the free encyclopediaor4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
Flashcard 149624659
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itSpot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega Theta Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue.<
Original toplevel document
Greeks (finance) - Wikipedia, the free encyclopediaor4.2 Speed4.3 Ultima4.4 Zomma 5 Greeks for multi-asset options6 Formulas for European option Greeks7 Related measures 7.1 Bond duration and convexity7.2 Beta7.3 Fugit 8 See also9 Notes10 References11 External links Use of the Greeks[edit] <span>Spot Price (S)Volatility ()Time to Expiry ()Value (V) Delta Vega ThetaDelta () GammaVannaCharmVega () VannaVommaVetaGamma () SpeedZommaColorVomma UltimaTotto Definition of Greeks as the sensitivity of an option's price and risk (in the first column) to the underlying parameter (in the first row). First-order Greeks are in blue, second-order Greeks are in green, and third-order Greeks are in yellow. Note that vanna appears twice as it should, and rho is left out as it is not as important as the rest. The Greeks are vital tools in risk management. Each Greek measures the sensitivity of the value of a portfolio to a small change in a given underlying parameter, so that component risks
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity (economics) - Wikipedia, the free encyclopedia
han 1) is one which responds more than proportionally to changes in other variables. In contrast, an inelastic variable (or elasticity value less than 1) is one which changes less than proportionally in response to changes in other variables. <span>Elasticity can be quantified as the ratio of the percentage change in one variable to the percentage change in another variable, when the latter variable has a causal influence on the former. A more precise definition is given in terms of differential calculus. It is a tool for measuring the responsiveness of one variable to changes in another, causative variable. Elasticit
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity of a function - Wikipedia, the free encyclopedia
er:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ Elasticity of a function From Wikipedia, the free encyclopedia Jump to: navigation, search <span>In mathematics, the elasticity or point elasticity of a positive differentiable function f of a positive variable (positive input, positive output)[1] at point a is defined as[2] or equivalently It is thus the ratio of the relative (percentage) change in the function's output with respect to the relative change in its input , for infinitesimal changes from a point . Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. The elasticity of a function is a constant if and only if the function has the form for a constant . The elasticity at a point is the limit of the arc elasticity between two points as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity of a function - Wikipedia, the free encyclopedia
ependent variable P on the vertical axis and the dependent variable Q on the horizontal axis, then the opposite rules would apply. The same graphical procedure can also be applied to a supply function or other functions. Semi-elasticity[edit] <span>A semi-elasticity (or semielasticity) gives the percentage change in f(x) in terms of a change (not percentage-wise) of x. Algebraically, the semi-elasticity S of a function f at point x is [4][5] An example of semi-elasticity is modified duration in bond trading. The term "semi-elasticity" is also sometimes used for the change if f(x) in terms of a percentage change in
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity (economics) - Wikipedia, the free encyclopedia
ble, when the latter variable has a causal influence on the former. A more precise definition is given in terms of differential calculus. It is a tool for measuring the responsiveness of one variable to changes in another, causative variable. <span>Elasticity has the advantage of being a unitless ratio, independent of the type of quantities being varied. Frequently used elasticities include price elasticity of demand, price elasticity of supply, income elasticity of demand, elasticity of substitution between factors of production and ela
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity (economics) - Wikipedia, the free encyclopedia
of wealth and different types of goods as they relate to the theory of consumer choice. Elasticity is also crucially important in any discussion of welfare distribution, in particular consumer surplus, producer surplus, or government surplus. <span>In empirical work an elasticity is the estimated coefficient in a linear regression equation where both the dependent variable and the independent variable are in natural logs. Elasticity is a popular tool among empiricists because it is independent of units and thus simplifies data analysis. A major study of the price elasticity of supply and the price elastic
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
ge point change in yield per year (for example yield going from 8% per year (y = 0.08) to 9% per year (y = 0.09)). This will give modified duration close to the value of Macaulay duration (and the same when rates are continuously compounded). <span>Formally, modified duration is a semi-elasticity, the percent change in price for a unit change in yield, rather than an elasticity, which is a percentage change in output for a percentage change in input. Modified duration is a rate of change, the percent change in price per change in yield. In derivatives pricing ("The Greeks"), the closest analogous quantity is Rho, which is the price elasticity (percentage change in price for percentage change in interest rate),
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
he percent change in price for a unit change in yield, rather than an elasticity, which is a percentage change in output for a percentage change in input. Modified duration is a rate of change, the percent change in price per change in yield. <span>In derivatives pricing ("The Greeks"), the closest analogous quantity is Rho, which is the price elasticity (percentage change in price for percentage change in interest rate), and, unlike modified duration, is an actual elasticity. Non-Fixed Cash Flows[edit] Modified duration can be extended to instruments with non-fixed cash flows, while Macaulay duration applies only to fixed cash flow instruments. Modified durat
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
fined above as a derivative (as the term relates to calculus) and so is based on infinitesimal changes. Modified duration is also useful as a measure of the sensitivity of a bond's market price to finite interest rate (i.e., yield) movements. <span>For a small change in yield, , Thus modified duration is approximately equal to the percentage change in price for a given finite change in yield. So a 15-year bond with a Macaulay duration of 7 years would have a Mod
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
a 15-year bond with a Macaulay duration of 7 years would have a Modified duration of roughly 7% and would fall approximately 7% in value if the interest rate increased by one percentage point (say from 7% to 8%).[6] Fisher-Weil Duration[edit] <span>Fisher-Weil duration is a refinement of Macaulay’s duration which takes into account the term structure of interest rates.Fisher-Weil duration calculates the present values of the relevant cashflows (more strictly) by using the zero coupon yield for each respective maturity.[7] Key Rate Duration[edit] Key r
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
ly 7% in value if the interest rate increased by one percentage point (say from 7% to 8%).[6] Fisher-Weil Duration[edit] Fisher-Weil duration is a refinement of Macaulay’s duration which takes into account the term structure of interest rates.<span>Fisher-Weil duration calculates the present values of the relevant cashflows (more strictly) by using the zero coupon yield for each respective maturity.[7] Key Rate Duration[edit] Key rate durations (also called partial DV01s or partial durations) are a natural extension of the total modified duration to measuring sensitivity to shifts
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
ey are and the final large circle including the final principal repayment. If these circles were put on a balance beam, the fulcrum of the beam would represent the weighted average distance (time to payment), which is 1.78 years in this case. <span>For most practical calculations, the Macaulay duration is calculated using the yield to maturity to calculate the : (2) (3) where: indexes the cash flows, is the present value of the th cash payment from an asset, is the cash flow of the th payment from an asset, is the y
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
which takes into account the term structure of interest rates.Fisher-Weil duration calculates the present values of the relevant cashflows (more strictly) by using the zero coupon yield for each respective maturity.[7] Key Rate Duration[edit] <span>Key rate durations (also called partial DV01s or partial durations) are a natural extension of the total modified duration to measuring sensitivity to shifts of different parts of the yield curve. Key rate durations might be defined, for example, with respect to zero-coupon rates with maturity '1M', '3M', '6M', '1Y', '2Y', '3Y', '5Y', '7Y', '10Y', '15Y', '20Y', '25Y', '30Y'. Ho (1992) [8] introduced the term key rate duration. Reitano covered multifactor yield curve models as early as 1991 [9] and has revisited the topic in a recent review.[10] Key rate dura
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
ar change in price for a $100 nominal bond for a one percentage point change in yield, is ($ per 1 percentage point change in yield) where the division by 100 is because modified duration is the percentage change. Dollar duration, DV01[edit] <span>The dollar duration or DV01 is defined as negative of the derivative of the value with respect to yield: so that it is the product of the modified duration and the price (value): ($ per 1 percentage point change in yield) or ($ per 1 basis point change in yield) The DV01 is analogous to the delta in derivative pricing (The Greeks) – it is the ratio of a price change in output (dollars) to unit change in input (a basis point of yield). Dollar dur
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
DV01 is defined as negative of the derivative of the value with respect to yield: so that it is the product of the modified duration and the price (value): ($ per 1 percentage point change in yield) or ($ per 1 basis point change in yield) <span>The DV01 is analogous to the delta in derivative pricing (The Greeks) – it is the ratio of a price change in output (dollars) to unit change in input (a basis point of yield). Dollar duration or DV01 is the change in price in dollars, not in p
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
to yield: so that it is the product of the modified duration and the price (value): ($ per 1 percentage point change in yield) or ($ per 1 basis point change in yield) The DV01 is analogous to the delta in derivative pricing (The Greeks) – <span>it is the ratio of a price change in output (dollars) to unit change in input (a basis point of yield). Dollar duration or DV01 is the change in price in dollars, not in percentage. It gives the dollar variation in a bond's value per unit change in the yield. It is often measured per 1 bas
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
e point change in yield) or ($ per 1 basis point change in yield) The DV01 is analogous to the delta in derivative pricing (The Greeks) – it is the ratio of a price change in output (dollars) to unit change in input (a basis point of yield). <span>Dollar duration or DV01 is the change in price in dollars, not in percentage. It gives the dollar variation in a bond's value per unit change in the yield. It is often measured per 1 basis point - DV01 is short for "dollar value of an 01" (or 1 basis poi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
nit change in input (a basis point of yield). Dollar duration or DV01 is the change in price in dollars, not in percentage. It gives the dollar variation in a bond's value per unit change in the yield. It is often measured per 1 basis point - <span>DV01 is short for "dollar value of an 01" (or 1 basis point). The names BPV (basis point value) or PV01 (present value of an 01) are also used, although PV01 more accurately refers to the value of a one dollar or one basis point annuity. (For a par
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
the change in price in dollars, not in percentage. It gives the dollar variation in a bond's value per unit change in the yield. It is often measured per 1 basis point - DV01 is short for "dollar value of an 01" (or 1 basis point). <span>The names BPV (basis point value) or PV01 (present value of an 01) are also used, although PV01 more accurately refers to the value of a one dollar or one basis point annuity. (For a par bond and a flat yield curve the DV01, derivative of price w.r.t. yield, and PV01, value of a one-dollar annuity, will actually have the same value.[citation needed]) DV01 or dollar duration can be used for instruments with zero up-front value such as interest rate swaps where percentage changes and modified duration are less usefu
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond convexity - Wikipedia, the free encyclopedia
: navigation, search This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2007) In finance, <span>bond convexity is a measure of the sensitivity of the duration of a bond to changes in interest rates, the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the higher the convexity, the more sensitive the bond pric
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond convexity - Wikipedia, the free encyclopedia
elp improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2007) In finance, bond convexity is a measure of the sensitivity of the duration of a bond to changes in interest rates, <span>the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the higher the convexity, the more sensitive the bond price is to the change in interest rates. Bond convexity is one of the most basic and widely used forms of convexity i
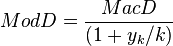
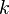 is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),
is the compounding frequency per year (1 for annual, 2 for semi-annual, 12 for monthly, 52 for weekly, etc.),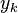 is the yield to maturity for an asset, periodically compounded
is the yield to maturity for an asset, periodically compounded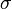 )
)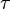 )
)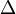
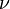
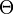
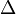 )
) 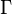
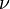 )
) 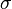 )
)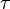 )
)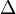
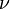
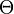
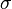 )
)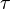 )
)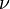
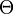
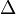
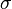 )
)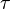 )
)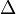
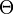
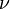
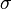 )
)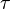 )
)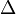
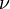
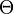
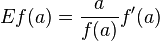
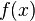 with respect to the relative change in its input
with respect to the relative change in its input 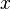 , for infinitesimal changes from a point
, for infinitesimal changes from a point 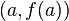 .
. 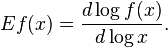
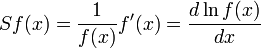
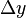 ,
,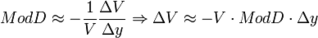
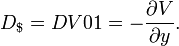
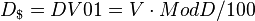 ($ per 1 percentage point change in yield)
($ per 1 percentage point change in yield)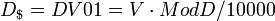 ($ per 1 basis point change in yield)
($ per 1 basis point change in yield)