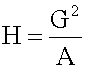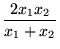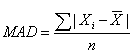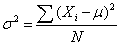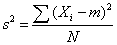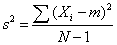BuboFlash - helps with learning

Edited, memorised or added to reading queue

Do you want BuboFlash to help you learning these things? Click here to log in or create user.

Flashcard 1621391707404

Tags

#tvm

Question

The [...] compensates investors for the increased sensitivity of the market value of debt to a change in market interest rates.

Answer

maturity premium

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1633823362316

Tags

#reading-7-discounted-cashflows-applications

Question

Periodic bond yields for both straight and zero-coupon bonds are conventionally computed based on [...]

Answer

semi-annual periods

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 5. Bond Equivalent Yield
Periodic bond yields for both straight and zero-coupon bonds are conventionally computed based on semi-annual periods, as U.S. bonds typically make two coupon payments per year. For example, a zero-coupon bond with a maturity of five years will mature in 10 6-month periods. The periodic yield for that

Flashcard 1636484648204

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In the [...] the midpoint of each class (interval) is shown on the horizontal (x) axis.

Answer

Frequency Polygon

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Frequency Distributions
f graphically displaying data. It is similar to a histogram but the bars are replaced by a line joined together. It is constructed in the following manner: Absolute frequency for each interval is plotted on the vertical (y) axis. The midpoint of each class (interval) is shown on the horizontal (x) axis. Neighboring points are connected with a straight line. Unlike a histogram, a frequency polygon adds a degree of continuity to the presentation of the distribution. It

Flashcard 1636822027532

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In a frequency distribution If too few intervals are used, [...].

Answer

too much data may be summarized and we may lose important characteristics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
In a frequency distribution It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough.

Original toplevel document

Subject 3. Frequency Distributions
that: Each observation can only lie in one interval. The total number of intervals will incorporate the whole population. The range for an interval is unique. This means a value (observation) can only fall into one interval. It is important to consider the number of intervals to be used. If too few intervals are used, too much data may be summarized and we may lose important characteristics; if too many intervals are used, we may not summarize enough. A frequency distribution is constructed by dividing the scores into intervals and counting the number of scores in each interval. The actual number of scores and the percent

Flashcard 1636830416140

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The following steps are required when organizing data into a frequency distribution.

Identify the highest and lowest values of the observations
[...]
Add up the number of observations and assign each observation to its class.
Count the number of observations in each class.

Answer

Setup classes (groups into which data is divided).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign

Original toplevel document

Subject 3. Frequency Distributions
by the total number of observations. Cumulative absolute frequency and cumulative relative frequency are the results from cumulating the absolute and relative frequencies as we move from the first to the last interval. The following steps are required when organizing data into a frequency distribution together with suggestions on constructing the frequency distribution. Identify the highest and lowest values of the observations. Setup classes (groups into which data is divided). The classes must be mutually exclusive and of equal size. Add up the number of observations and assign each observation to its class. Count the number of observations in each class. This is called the class frequency. Data can be divided into two types: discrete and continuous. Discrete: The values in the data set can be counted. There are distinct spaces between the values, such as

Flashcard 1640946339084

Question

RTE Act is applicable to which age group?

Answer

The RTE Act, 2009 envisages free and compulsory elementary education to every child in the age group of 6-14 years

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Daily Current Affairs for IAS UPSC Exam Preparation – Civilsdaily
recommendations Better monitoring of funds allocated. Centre and states to finalize an annual work plan and budget for RTE in alignment with the Union budget for better coordination and utilization. Back2basics The RTE Act, 2009 The RTE Act, 2009 envisages free and compulsory elementary education to every child in the age group of 6-14 years . The section 23(2) of the Act specifies that all teachers at elementary level at commencement of this law if did not possess minimum qualifications under it need to acquire these w

Annotation 1640983301388

#fta #un #wto

Trade Facilitation Agreement (TFA)

The TFA is the WTO’s first-ever multilateral accord that aims to simplify customs regulations for the cross-border movement of goods. It was outcome of WTO’s 9th Bali (Indonesia) ministerial package of 2013
The agreement includes provisions for Lowering import tariffs and agricultural subsidies: It will make it easier for developing countries to trade with the developed world in global markets
Abolish hard import quotas: Developed countries would abolish hard import quotas on agricultural products from the developing world and instead would only be allowed to charge tariffs on amount of agricultural imports exceeding specific limits
Reduction in red tape at international borders: It aims to reduce red-tapism to facilitate trade by reforming customs bureaucracies and formalities

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Daily Current Affairs for IAS UPSC Exam Preparation – Civilsdaily
s reforms and modernization The WCO maintains the international Harmonized System (HS) goods nomenclature, and administers the technical aspects of the World Trade Organization (WTO) Agreements on Customs Valuation and Rules of Origin Trade Facilitation Agreement (TFA) The TFA is the WTO’s first-ever multilateral accord that aims to simplify customs regulations for the cross-border movement of goods. It was outcome of WTO’s 9th Bali (Indonesia) ministerial package of 2013 The agreement includes provisions for Lowering import tariffs and agricultural subsidies: It will make it easier for developing countries to trade with the developed world in global markets Abolish hard import quotas: Developed countries would abolish hard import quotas on agricultural products from the developing world and instead would only be allowed to charge tariffs on amount of agricultural imports exceeding specific limits Reduction in red tape at international borders: It aims to reduce red-tapism to facilitate trade by reforming customs bureaucracies and formalities. The Hindu July 22, 2017 [op-ed snap] The need for lateral entry in civil services [imagelink] Image source Note4studert

Flashcard 1641148976396

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The periodic investment of a fixed amount of money.

Answer

Cost averaging

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1641150811404

#reading-8-statistical-concepts-and-market-returns

The harmonic mean is a relatively specialized concept of the mean that is appropriate when averaging ratios (“amount per unit”) when the ratios are repeatedly applied to a fixed quantity to yield a variable number of units.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1641155005708

Dollar-cost averaging (DCA) is an investment technique of buying a fixed dollar amount of a particular investment on a regular schedule, regardless of the share price. The investor purchases more shares when prices are low and fewer shares when prices are high. The premise is that DCA lowers the average share cost over time, increasing the opportunity to profit. The DCA technique does not guarantee that an investor won't lose money on investments. Rather, it is meant to allow investment over time instead of investment as a lump sum.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Dollar-Cost Averaging (DCA)
What is 'Dollar-Cost Averaging - DCA' Dollar-cost averaging (DCA) is an investment technique of buying a fixed dollar amount of a particular investment on a regular schedule, regardless of the share price. The investor purchases more shares when prices are low and fewer shares when prices are high. The premise is that DCA lowers the average share cost over time, increasing the opportunity to profit. The DCA technique does not guarantee that an investor won't lose money on investments. Rather, it is meant to allow investment over time instead of investment as a lump sum. BREAKING DOWN 'Dollar-Cost Averaging - DCA' Fundamental to the strategy is a commitment to investing a fixed dollar amount each month. Depending

Flashcard 1641157102860

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Unless all the observations in a data set have the same value, the [...] is less than the geometric mean

Answer

harmonic mean

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641158937868

Tags

#reading-8-statistical-concepts-and-market-returns

Question

What is a good example on when to use the Harmonic Mean?

Answer

Cost Averaging (lo que hiciste con Javier)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641160772876

Tags

#has-images #quantitative-methods-basic-concepts #statistics

Question

For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by:

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
rs x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: <body><html>

Original toplevel document

Subject 4. Measures of Center Tendency
, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist

Flashcard 1641163132172

Tags

#has-images #quantitative-methods-basic-concepts #statistics

Question

The special cases of n = 2 Harmonic Mean

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mea

Original toplevel document

Flashcard 1641164705036

Tags

#has-images #quantitative-methods-basic-concepts #statistics

Question

The special cases of n = 3 for the Harmonic Mean are given by:

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Original toplevel document

Flashcard 1641167588620

Tags

#reading-8-statistical-concepts-and-market-returns

Question

If talking about a Survey is it a population or a sample?

Answer

Sample

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1641169423628

#reading-8-statistical-concepts-and-market-returns

What are the reasons for sampling?

Sampling is used when:

1. The population is infinite.
2. There is a limited amount of time available.
3. The nature of the test is destructive.
4. The cost of gathering the data is a factor.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1641171520780

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When in a histograms there are only midpoints showing how do you find out the interval width?

Answer

substract any Midpoint - Midpoint_-1and you have the interval width.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641173355788

Tags

#reading-8-statistical-concepts-and-market-returns

Question

What is class mark in a Frequency distribution?

Answer

The average of the values of the class limits

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641175190796

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The class mark is also called [...]

Answer

Midvalue or central value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641179909388

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Quantiles that divide a distribution into four equal parts.

Answer

Quartiles

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641181744396

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Quantiles that divide a distribution into five equal parts.

Answer

Quintiles

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641183579404

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Quantiles that divide a distribution into 100 equal parts.

Answer

Percentiles

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641185414412

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Given a set of observations, how many observations lie below the 33th percentile?

Answer

33%

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1641188035852

#reading-8-statistical-concepts-and-market-returns

When dealing with actual data, we often find that we need to approximate the value of a percentile. For example, if we are interested in the value of the 75th percentile, we may find that no observation divides the sample such that exactly 75 percent of the observations lie at or below that value. The following procedure, however, can help us determine or estimate a percentile. The procedure involves first locating the position of the percentile within the set of observations and then determining (or estimating) the value associated with that position.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1641189870860

Tags

#reading-8-statistical-concepts-and-market-returns

Question

We know that the median divides a distribution in half. We can define other dividing lines that split the distribution into smaller sizes called [...]

Answer

Quantiles

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641191705868

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The formula for the position of a percentile in an array with n entries sorted in ascending order is

L_y = [...]

Answer

(n+1) ^y/₁₀₀

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641193540876

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The value of L_y may or may not be a [...]

Answer

whole number.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641195375884

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In general, as the sample size increases, the percentile location calculation becomes [...]

Answer

more accurate;

in small samples it may be quite approximate.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641197210892

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When the location, L_y, is a whole number, the location corresponds to [...]

Answer

an actual observation.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641199045900

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When L_y is not a whole number or integer, L_y lies [...]

Answer

between the two closest integer numbers

(one above and one below)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641200880908

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When L_y is not a whole number or integer, L_y lies between the two closest integer numbers (one above and one below), and we use [...] between those two places to determine P_y.

Answer

linear interpolation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641202715916

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The estimation of an unknown value on the basis of two known values that bracket it, using a straight line between the two known values.

Answer

linear interpolation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641204550924

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Linear interpolation for a value of 12.75 for Py

Py ≈ [...]

Answer

X₁₂ + (12.75 − 12) (X₁₃ − X₁₂).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641206385932

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Using [...] we move the percent of the distance above the integer (e.g 12.75-12= 75%) from X₁₂ to X₁₃ as an estimate of P_y.

Answer

linear interpolation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641208220940

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The nearest whole numbers below and above L_y establish the positions of observations that bracket P_y and then [...] of those two observations.

Answer

interpolate between the values

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644271111436

He was committed to the scientific study of society, empirical research, and the search for causes of social phenomena. He devoted considerable attention to various social institu- tions (for example, politics, economy) and their interrelationships. He was inter- ested in comparing primitive and modern societies

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 1644272684300

Ibn-Khaldun stressed the importance of linking socio- logical thought and historical observation

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 1644274257164

he served a variety of sultans in Tunis, Morocco, Spain, and Algeria as ambassador, chamberlain, and member of the scholars’ council. He also spent two years in prison in Morocco for his belief that state rulers were not divine leaders

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 1644295752972

Investment styles

#reading-8-statistical-concepts-and-market-returns

(1) firm size (buying stocks of small firms and selling stocks of large firms),

(2) value/growth (buying stocks of value firms, defined as firms for which the stock price is relatively low in relation to earnings per share, book value per share, or dividends per share, and selling stocks of growth firms, defined as firms for which the stock price is relatively high in relation to those same measures)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644297587980

Investment styles

#reading-8-statistical-concepts-and-market-returns

As the well-known researcher Fischer Black has written, “[t]he key issue in investments is estimating expected return.”

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644299422988

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The mean tells us where returns are centered but, to completely understand an investment, we also need to know how returns are [...]

Answer

dispersed around the mean.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644301257996

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is the variability around the central tendency.

Answer

Dispersion

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644303093004

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The most common measures of dispersion: [...] , [...] , variance, and standard deviation.

Answer

mean absolute deviation

range

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644304928012

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The most common measures of dispersion: mean absolute deviation, [...], range and [...]

Answer

variance

standard deviation.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644306763020

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The amount of variability present without comparison to any reference point or benchmark.

Answer

Absolute Dispersion

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644308598028

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The [...] or [...] of return is often used as a measure of risk pioneered by Nobel laureate Harry Markowitz.

Answer

variance

standard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644310695180

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The simplest of all the measures of dispersion is [...]

Answer

range

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644312005900

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Range can be computed with [...] or [...] data.

Answer

interval

ratio

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644315413772

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The difference between the maximum and minimum values in a dataset.

Answer

Range

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644317248780

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Range = [...]

Answer

Maximum value – Minimum value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644319083788

Tags

#reading-8-statistical-concepts-and-market-returns

Question

how the data are distributed is called the [...]

Answer

shape of the distribution

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644320918796

Interquartile Range

#reading-8-statistical-concepts-and-market-returns

Another distance measure of dispersion that we may encounter, the interquartile range, focuses on the middle rather than the extremes. The interquartile range (IQR) is the difference between the third and first quartiles of a data set: IQR = Q₃ − Q₁. The IQR represents the length of the interval containing the middle 50 percent of the data, with a larger interquartile range indicating greater dispersion, all else equal.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644322753804

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The interquartile range is a [...]

Answer

distance measure of dispersion

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644325113100

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The interquartile range, focuses on [...] rather than [...] .

Answer

The middle

the extremes

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Interquartile Range
Another distance measure of dispersion that we may encounter, the interquartile range, focuses on the middle rather than the extremes. The interquartile range (IQR) is the difference between the third and first quartiles of a data set: IQR = Q 3 − Q 1 . The IQR represents the length of the interval containing the mi

Flashcard 1644327472396

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The interquartile range (IQR) is the difference between [...]

Answer

the third and first quartiles of a data set

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644329831692

Tags

#reading-8-statistical-concepts-and-market-returns

Question

IQR = [...]

Answer

Q₃ − Q₁

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Interquartile Range
span>Another distance measure of dispersion that we may encounter, the interquartile range, focuses on the middle rather than the extremes. The interquartile range (IQR) is the difference between the third and first quartiles of a data set: IQR = Q 3 − Q 1 . The IQR represents the length of the interval containing the middle 50 percent of the data, with a larger interquartile range indicating greater dispersion, all else equal.</sp

Flashcard 1644332190988

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The IQR represents the length of the interval containing [...] of the data,

Answer

the middle 50 percent

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Interquartile Range
ce measure of dispersion that we may encounter, the interquartile range, focuses on the middle rather than the extremes. The interquartile range (IQR) is the difference between the third and first quartiles of a data set: IQR = Q 3 − Q 1 . The IQR represents the length of the interval containing the middle 50 percent of the data, with a larger interquartile range indicating greater dispersion, all else equal.<body><html>

Flashcard 1644334550284

Tags

#reading-8-statistical-concepts-and-market-returns

Question

All else equal, a larger interquartile range indicaties [...]

Answer

greater dispersion.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Interquartile Range
le rather than the extremes. The interquartile range (IQR) is the difference between the third and first quartiles of a data set: IQR = Q 3 − Q 1 . The IQR represents the length of the interval containing the middle 50 percent of the data, with a larger interquartile range indicating greater dispersion, all else equal.<body><html>

Flashcard 1644336909580

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The difference between the third and first quartiles of a dataset.

Answer

Interquatile range

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644338744588

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Why don't we compute measures of dispersion as the arithmetic average of the deviations around the mean?

Answer

The deviations around the mean always sum to 0.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644340579596

Tags

#reading-8-statistical-concepts-and-market-returns

Question

With reference to a sample, the mean of the absolute values of deviations from the sample mean.

Answer

Mean Absolute Deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Article 1644342676748

Subject 6. Measures of Dispersion
#has-images #reading-8-statistical-concepts-and-market-returns

Dispersion is defined as "variability around the central tendency." Investment is all about reward versus variability (risk). A central tendency is a measure of the reward of an investment and dispersion is a measure of investment risk. There are two types of dispersions: Absolute dispersion is the amount of variability without comparison to any benchmark. Measures of absolute dispersion include range, mean absolute deviation, variance, and standard deviation. Relative dispersion is the amount of variability in comparison to a benchmark. Measures of relative dispersion include the coefficient of variance. The range is the simplest measure of spread or dispersion. It is equal to the difference between the largest and the smallest values. The range can be a useful measure of spread because it is so easily understood. However, it is very sensitive to extreme scores because it is based on only two values. It also cannot reveal the shape of the distribution. The range should almost never be u

Flashcard 1644351851788

Tags

#has-images #reading-8-statistical-concepts-and-market-returns

Question

The mean absolute deviation formula

MAD = [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 6. Measures of Dispersion
artile range. Example The range of the numbers 1, 2, 4, 6,12,15,19, 26 = 26 - 1 = 25 Recall that the deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The mean absolute deviation (MAD) is the arithmetic average of the absolute deviations around the mean. In calculating the MAD, we ignore the signs of deviations around the mean. Remember that the sum of all the deviations from the mean is equal to

Flashcard 1644353424652

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The mean absolute deviation (MAD) is the [...] of [...]

Answer

arithmetic average

the absolute deviations around the mean.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644356046092

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In calculating MAD, we ignore [...] of the deviations around the mean.

Answer

the signs

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644357881100

Tags

#reading-8-statistical-concepts-and-market-returns

Question

One technical drawback of MAD is that it is difficult to manipulate mathematically compared with the [...] .

Answer

variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644359716108

In some analytic work such as optimization, the calculus operation of differentiation is important. Variance as a function can be differentiated, but absolute value cannot.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644362075404

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A second approach to the treatment of deviations adding up to 0 is to [...]

Answer

square them.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644363910412

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The expected value of squared deviations from a random variable’s expected value.

Answer

Variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644366007564

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is defined as the average of the squared deviations around the mean

Answer

Variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644367842572

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is the positive square root of the variance.

Answer

Standard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644369677580

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The positive square root of the variance; a measure of dispersion in the same units as the original data.

Answer

Standard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644371512588

Tags

#has-images #reading-8-statistical-concepts-and-market-returns

Question

The formula for the variance in a population is

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 6. Measures of Dispersion
ons in the sample. However, the absolute value is difficult to work with mathematically. The variance is a measure of how spread out a distribution is. It is computed as the average squared deviation of each number from its mean. The formula for the variance in a population is where: μ = the mean N = the number of scores When the variance is computed in a sample, the statistic(m = the mean of the sample) can be used

Flashcard 1644373871884

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Because the variance is measured in squared units, we need a way to return to the original units thus the [...]

Answer

Standard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644375706892

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Standard deviation is the [...]

Answer

square root of the variance.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644377541900

Tags

#has-images #reading-8-statistical-concepts-and-market-returns

Question

When the variance is computed in a sample, the formula is [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 6. Measures of Dispersion
read out a distribution is. It is computed as the average squared deviation of each number from its mean. The formula for the variance in a population is where: μ = the mean N = the number of scores When the variance is computed in a sample, the statistic(m = the mean of the sample) can be used. However, s 2 is a biased estimate of σ 2 . By far the most common formula for computing variance in a sample is: &#13

Annotation 1644380163340

Forbes magazine annually selects US equity mutual funds meeting certain criteria for its Honor Roll. The criteria relate to capital preservation (performance in bear markets), continuity of management (the fund must have a manager with at least six years’ tenure), diversification, accessibility (disqualifying funds that are closed to new investors), and after-tax long-term performance.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644381998348

We could not properly use the Honor Roll funds to estimate the population variance of portfolio turnover (for example) of any other differently defined population, because the Honor Roll funds are not a random sample from any larger population of US equity mutual funds.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644383833356

Tags

#reading-8-statistical-concepts-and-market-returns

Question

We use [...] to symbolize sample quantities.

Answer

Roman letters

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644386454796

Tags

#has-images #reading-8-statistical-concepts-and-market-returns

Question

The formula for computing variance in a sample is:

s^{2 =} [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 6. Measures of Dispersion
n is where: μ = the mean N = the number of scores When the variance is computed in a sample, the statistic(m = the mean of the sample) can be used. However, s 2 is a biased estimate of σ 2 . By far the most common formula for computing variance in a sample is: This gives an unbiased estimate of σ 2 . Since samples are usually used to estimate parameters, s 2 is the most commonly used measure of variance

Annotation 1644388814092

#reading-8-statistical-concepts-and-market-returns

In the math of statistics, using only N in the denominator when using a sample to represent its population will result in underestimating the population variance, especially for small sample sizes. This systematic understatement causes the sample variance to be a biased estimator of the population variance. By using (N - 1) instead of N in the denominator, we compensate for this underestimation. Thus, using N - 1, the sample variance (s²) will be an unbiased estimator of the population variance (σ²).

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Subject 6. Measures of Dispersion
tion variance except for the use of the sample mean, X, and the denominator. In the case of the population variance, we divide by the size of the population, N. For the sample variance, however, we divide by the sample size minus 1, or N - 1. In the math of statistics, using only N in the denominator when using a sample to represent its population will result in underestimating the population variance, especially for small sample sizes. This systematic understatement causes the sample variance to be a biased estimator of the population variance. By using (N - 1) instead of N in the denominator, we compensate for this underestimation. Thus, using N - 1, the sample variance (s 2 ) will be an unbiased estimator of the population variance (σ 2 ). The major problem with using the variance is the difficulty interpreting it. Why? The variance, unlike the mean, is in terms of units squared. How does one interpret square

Flashcard 1644390386956

Tags

#reading-8-statistical-concepts-and-market-returns

Question

By using [...] , we improve the statistical properties of the sample variance.

Answer

n − 1 (rather than n) as the divisor

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644392221964

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The quantity n − 1 is also known as the number of [...] in estimating the population variance.

Answer

degrees of freedom

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644394056972

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Once we have computed the sample mean, there are only [...] independent deviations from it.

Answer

n − 1

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644395891980

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The sample standard deviation is [...]

Answer

The positive square root of the sample variance.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644397726988

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The mean absolute deviation will always be less than or equal to the standard deviation because [...]

Answer

standard deviation gives more weight to large deviations than to small ones

(remember, the deviations are squared).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644399037708

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The mean absolute deviation will always be [...] to the standard deviation

Answer

less than or equal

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644402183436

Because the standard deviation is a measure of dispersion about the arithmetic mean, we usually present the arithmetic mean and standard deviation together when summarizing data. When we are dealing with data that represent a time series of percent changes, presenting the geometric mean—representing the compound rate of growth—is also very helpful.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644404804876

Variance and standard deviation of returns take account of returns above and below the mean, but investors are concerned only with downside risk, for example, returns below the mean. As a result, analysts have developed semivariance, semideviation, and related dispersion measures that focus on downside risk.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644406639884

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is defined as the average squared deviation below the mean.

Answer

Semivariance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644408474892

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is the positive square root of semivariance.

Answer

Semideviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644410309900

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Semideviation is sometimes called [...]

Answer

Semistandard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644412144908

Tags

#reading-8-statistical-concepts-and-market-returns

Question

To compute the sample semivariance, for example, we take the following steps:

Calculate the sample mean.
[...] .
Compute the sum of the squared negative deviations from the mean.
Divide the sum from Step iii by [...] .

Answer

Identify the observations that are smaller than or equal to the mean (discarding observations greater than the mean)

the total sample size minus 1: n − 1

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644413979916

#reading-8-statistical-concepts-and-market-returns

An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Subject 6. Measures of Dispersion
variance indicates the adequacy of the mean as representative of the population by measuring the deviation from expectation. Basically, the variance and the standard deviation are measures of the average deviation from the mean. An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score. In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean.

Annotation 1644415552780

#reading-8-statistical-concepts-and-market-returns

In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Subject 6. Measures of Dispersion
An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score. In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean. The standard deviation has proven to be an extremely useful measure of spread in part because it is mathematically tractable. Many formulas in inferential statistics use th

Flashcard 1644417125644

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A formula for semivariance approximating the unbiased estimator is:

\(\sum (X_i-\bar {X}) \over n-1\)

for all [...]

Answer

Xi ≤ ¯X

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644419747084

For a group of of Selected American Shares with returns (in percent) the semideviation is 21.3% which is less than the standard deviation of 26.7%.

From this downside risk perspective, therefore, standard deviation overstates risk.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644421582092

In practice, we may be concerned with values of return (or another variable) below some level other than the mean. For example, if our return objective is 12.75 percent annually, we may be concerned particularly with returns below 12.75 percent a year. We can call 12.75 percent the target. The name target semivariance has been given to average squared deviation below a stated target, and target semideviation is its positive square root.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644423417100

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The average squared deviation below a target value.

Answer

Target Semivariance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644425252108

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The positive square root of target semivariance.

Answer

Target Semideviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644427087116

Tags

#reading-8-statistical-concepts-and-market-returns

Question

To calculate a sample target semivariance, what is the first step?

Answer

we specify the target as a first step.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644428922124

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A formula for target semivariance is

∑(Xi−B)² / (n−1)

for all [...]

Answer

Xi ≤ B

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644430757132

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When return distributions are symmetric, semivariance and variance are [...]

Answer

effectively equivalent.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644432592140

Tags

#reading-8-statistical-concepts-and-market-returns

Question

For asymmetric distributions, variance and semivariance rank [...]

Answer

prospects’ risk differently

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644434427148

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Semivariance (or semideviation) and target semivariance (or target semideviation) have intuitive appeal, but [...]

Answer

they are harder to work with mathematically than variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644436262156

We can find a portfolio’s variance as a straightforward function of the variances and correlations of the component securities.

We cannot do it for semivariance and target semivariance.

We also cannot take the derivative of semivariance or target semivariance.

Will be disscussed in probability.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644438097164

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Variance or standard deviation enters into the definition of many of the most commonly used finance risk concepts, such as the [...] and [...] .

Answer

Sharpe ratio

beta

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644439932172

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The Chebyshev inequality gives the proportion of values within [...] .

Answer

k standard deviations of the mean

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644441767180

According to Chebyshev’s inequality, for any distribution with finite variance, the proportion of the observations within k standard deviations of the arithmetic mean is at least 1 − 1/k² for all k > 1.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644444388620

Tags

#reading-8-statistical-concepts-and-market-returns

Question

According Chebyshev’s inequality a two-standard-deviation interval around the mean must contain at least [...] of the observations, and a three-standard-deviation interval around the mean must contain at least [...] of the observations, no matter how the data are distributed.

Answer

75 percent

89 percent

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644446223628

Chebyshev’s inequality holds for samples and populations and for discrete and continuous data regardless of the shape of the distribution.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644448058636

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Does Chebyshev’s inequality give the minimum of observations that must fall within a given interval around the mean?

Answer

yes

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644449893644

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Does Chebyshev’s inequality give the maximum of observations that must fall within a given interval around the mean?

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644451728652

We may sometimes find it difficult to interpret what standard deviation means in terms of the relative degree of variability of different sets of data, however, either because the data sets have markedly different means or because the data sets have different units of measurement.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644453563660

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is the amount of dispersion relative to a reference value or benchmark.

Answer

Relative dispersion

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644455398668

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Standard deviation (and variance) has the property of remaining unchanged if [...]

Answer

we add a constant amount to each observation.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644457233676

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The [...] is the ratio of the standard deviation of a set of observations to their mean value

Answer

coefficient of variation, CV

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644459068684

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Coefficient of Variation Formula.

CV= [...]

Answer

s/¯X

standard-deviation / Mean

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644460903692

Tags

#reading-8-statistical-concepts-and-market-returns

Question

When the observations are returns the coefficient of variation measures the amount of [...]

Answer

risk (standard deviation) per unit of mean return.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644462738700

Expressing the magnitude of variation among observations relative to their average size, the coefficient of variation permits direct comparisons of dispersion across different data sets.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644464573708

Tags

#reading-8-statistical-concepts-and-market-returns

Question

the coefficient of variation is a [...] measure

Answer

scale-free

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644466408716

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A higher coefficient of variation means that sample has [...] than the other sample.

Answer

greater variability (dispersion) in whatever is being measured

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644468243724

CV vs Standard Deviation

Hong Kong s=22.24, CV = 2.383

Singapoure s=19.2, CV = 2.065

As measured both by standard deviation and CV, Hong Kong market was riskier than the Singapore market. The standard deviation of Hong Kong returns was (22.4 − 19.2)/19.2 = 0.167 or about 17 percent larger than Singapore returns, compared with a difference in the CV of (2.383 − 2.065)/2.065 = 0.154 or about 15 percent. Thus, the CVs reveal slightly less difference between Hong Kong and Singapore return variability than that suggested by the standard deviations alone.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644471651596

#reading-8-statistical-concepts-and-market-returns

Although CV was designed as a measure of relative dispersion, its inverse reveals something about return per unit of risk.

For example, a portfolio with a mean monthly return of 1.19 percent and a standard deviation of 4.42 percent has an inverse CV of 1.19%/4.42% = 0.27. This result indicates that each unit of standard deviation represents a 0.27 percent return.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644474273036

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A more precise return–risk measure than the CV recognizes the existence of [...]

Answer

a risk-free return, a return for virtually zero standard deviation.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644476108044

#reading-8-statistical-concepts-and-market-returns

With a risk-free asset, an investor can choose a risky portfolio, p, and then combine that portfolio with the risk-free asset to achieve any desired level of absolute risk as measured by standard deviation of return, s_p.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Annotation 1644477943052

#reading-8-statistical-concepts-and-market-returns

Consider a graph with mean return on the vertical axis and standard deviation of return on the horizontal axis. Any combination of portfolio p and the risk-free asset lies on a ray (line) with slope equal to the quantity (Mean return − Risk-free return) divided by s_p. The ray giving investors choices offering the most reward (return in excess of the risk-free rate) per unit of risk is the one with the highest slope. The ratio of excess return to standard deviation of return for a portfolio p—the slope of the ray passing through p—is a single-number measure of a portfolio’s performance known as the Sharpe ratio, after its developer, William F. Sharpe.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644479778060

Tags

#reading-8-statistical-concepts-and-market-returns

Question

spread from or as if from a central point.

Answer

ray

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644482399500

Tags

#reading-8-statistical-concepts-and-market-returns

Question

a measure of the average excess return earned per unit of standard deviation of return.

Answer

Sharpe Ratio

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644484234508

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Sharpe Ratio Formula.

Sh = R_p − R_F/ s_p

Rp = [...]

R_F = [...]

s_p= [...]

Answer

R_p = the mean return to the portfolio

RF = is the mean return to a risk-free asset,

S_{p =}standard deviation of return on the portfolio

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644486069516

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Sharpe Ratio Formula.

S_h = [...]

Answer

R_p − R_F/ s_p

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644487904524

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The average rate of return in excess of the risk-free rate.

Answer

Mean excess return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644489739532

Tags

#reading-8-statistical-concepts-and-market-returns

Question

the Sharpe ratio measures the reward in terms of [...] per [...]

Answer

unit of risk

mean excess return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644491574540

Tags

#reading-8-statistical-concepts-and-market-returns

Question

We often find that portfolios exhibit negative Sharpe ratios when it is calculated over periods in which [...]

Answer

bear markets for equities dominate.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644493409548

Tags

#reading-8-statistical-concepts-and-market-returns

Question

What happens to a portfolio's positive Sharpe ratio if we increase risk

Answer

Sharpe ratio decreases if we increase risk, all else equal

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644495244556

Tags

#reading-8-statistical-concepts-and-market-returns

Question

With negative Sharpe ratios, increasing risk results in a [...]

Answer

numerically larger Sharpe ratio

( doubling risk may increase the Sharpe ratio from −1 to −0.5).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644497079564

#reading-8-statistical-concepts-and-market-returns

To make an interpretable comparison in cases with negative Sharpe ratio, we may need to increase the evaluation period such that one or more of the Sharpe ratios becomes positive; we might also consider using a different performance evaluation metric.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644498914572

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The conceptual limitation of the Sharpe ratio is that it [...]

Answer

considers only one aspect of risk, standard deviation of return.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644500749580

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] is most appropriate as a risk measure for portfolio strategies with approximately symmetric return distributions.

Answer

Standard deviation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644502584588

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Strategies with option elements have [...] returns.

Answer

asymmetric returns

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644504419596

#reading-8-statistical-concepts-and-market-returns

Relatedly, an investment strategy may produce frequent small gains but have the potential for infrequent but extremely large losses. Such a strategy is sometimes described as picking up coins in front of a bulldozer; for example, some hedge fund strategies tend to produce that return pattern. Calculated over a period in which the strategy is working (a large loss has not occurred), this type of strategy would have a high Sharpe ratio. In this case, the Sharpe ratio would give an overly optimistic picture of risk-adjusted performance because standard deviation would incompletely measure the risk assumed. Therefore, before applying the Sharpe ratio to evaluate a manager, we should judge whether standard deviation adequately describes the risk of the manager’s investment strategy.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644506254604

Question

One frequently used rule of thumb is to round a mean (or a standard deviation) to [...].

Answer

one additional decimal than the data

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644508089612

Question

5^-2 = [...] = [...]

Answer

1/(5²) = 1/25

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644509924620

Question

An exponent of ^1/2 is equivalent to [...]

Answer

The square root

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644511759628

Tags

#exponents

Question

Any number raised to 0 (y⁰) = [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644513594636

Tags

#exponents

Question

y^m * yⁿ = [...]

Answer

y^(n+m)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644515429644

Tags

#exponents

Question

(yⁿ)^m = [...]

Answer

y^(n*m)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644517264652

Tags

#exponents

Question

(y * x)ⁿ= [...]

Answer

yⁿ* xⁿ

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644519099660

Tags

#exponents

Question

A logarithm (of the base b) is the [...]

Answer

power to which the base needs to be raised to yield a given number.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644523031820

Tags

#math

Question

How many of one number do we multiply to get another number?

This question is answered by [...]

Answer

Logarithms

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644524866828

Tags

#logarithms

Question

How many 2s do we multiply to get 8?

2 × 2 × 2 = 8

write this mathematically

Answer

log₂(8) = 3

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644544003340

#reading-8-statistical-concepts-and-market-returns

In calculations of variance since the deviations around the mean are squared, we do not know whether large deviations are likely to be positive or negative.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644545838348

Tags

#reading-8-statistical-concepts-and-market-returns

Question

One important characteristic of interest to analysts is the degree of [...] in return distributions.

Answer

symmetry

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644547935500

#reading-8-statistical-concepts-and-market-returns

If a return distribution is symmetrical about its mean, then each side of the distribution is a mirror image of the other. Thus equal loss and gain intervals exhibit the same frequencies. Losses from −5 percent to −3 percent, for example, occur with about the same frequency as gains from 3 percent to 5 percent.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644550032652

Tags

#reading-8-statistical-concepts-and-market-returns

Question

As a mnemonic, in the case of skewness and distribution the mean, median, and mode occur [...]

Answer

in the same order as they would be listed in a dictionary.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644551867660

Tags

#reading-8-statistical-concepts-and-market-returns

Question

[...] means not symmetrical.

Answer

Skewed

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644553702668

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A return distribution with [...] has frequent small losses and a few extreme gains.

Answer

positive skew

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644555799820

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Which type of distribution is completely described by its mean and variance.

Answer

Normal distribution

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644557896972

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A return distribution with [...] has frequent small gains and a few extreme losses.

Answer

negative skew

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644560518412

Tags

#reading-8-statistical-concepts-and-market-returns

Question

skewness is computed using [...]

Answer

each observation’s deviation from its mean

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644562353420

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A quantitative measure of lack of symmetry

Answer

Skewness

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644564450572

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Skewness is computed as the [...] standardized by [...] to make the measure free of scale

Answer

average cubed deviation from the mean

dividing by the standard deviation cubed

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644566547724

#reading-8-statistical-concepts-and-market-returns

We are discussing a moment coefficient of skewness. Some textbooks present the Pearson coefficient of skewness, equal to 3(Mean − Median)/Standard deviation, which has the drawback of involving the calculation of the median.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644568382732

Tags

#reading-8-statistical-concepts-and-market-returns

Question

A symmetric distribution has skewness of [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644570217740

Tags

#reading-8-statistical-concepts-and-market-returns

Question

In Skewness formula we use cube because cubing, unlike squaring, [...]

Answer

preserves the sign of the deviations from the mean.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644572052748

#reading-8-statistical-concepts-and-market-returns

If a distribution is positively skewed with a mean greater than its median, then more than half of the deviations from the mean are negative and less than half are positive. In order for the sum to be positive, the losses must be small and likely, and the gains less likely but more extreme. Therefore, if skewness is positive, the average magnitude of positive deviations is larger than the average magnitude of negative deviations.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644574149900

Tags

#reading-8-statistical-concepts-and-market-returns

Question

The term n / [(n − 1)(n − 2)] in Skewness formula corrects for a [...]

Answer

downward bias in small samples.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644576247052

Tags

#reading-8-statistical-concepts-and-market-returns

Question

Sample Skewness Formula.

\(Sk = {n \over (n-1)(n-2)}\) [...]

Answer

\( {\Sigma(Xi-\bar{X})^3 \over s^3}\)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644577033484

Tags

#reading-8-statistical-concepts-and-market-returns

Question

What indicates the direction of skew?

Answer

algebraic sign in the formula result

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Annotation 1644580703500

#reading-8-statistical-concepts-and-market-returns

Note that as n becomes large, the expression reduces to the mean cubed deviation, SK ≈ (1/n) n∑_i=1(Xi−X)³/ s³ . As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Flashcard 1644583324940

Tags

#reading-8-statistical-concepts-and-market-returns

Question

As a reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of [...] would be considered unusually large.

Answer

±0.5

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Open it
Note that as n becomes large, the expression reduces to the mean cubed deviation, SK ≈ (1/n) n∑ i=1 (Xi−X) 3 / s 3 . As a frame of reference, for a sample size of 100 or larger taken from a normal distribution, a skewness coefficient of ±0.5 would be considered unusually large.

Annotation 1644585946380

#reading-8-statistical-concepts-and-market-returns

Some researchers believe that investors should prefer positive skewness, all else equal—that is, they should prefer portfolios with distributions offering a relatively large frequency of unusually large payoffs.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

Edited, memorised or added to reading queue

on 23-Jul-2017 (Sun)

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document

pdf

pdf

pdf