Edited, memorised or added to reading queue
on 02-Jul-2014 (Wed)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
d to add to the curve you are discounting with in order to generate a price that matches the market price. Conventionally, the zero rates are determined from the Treasury curve, with semi-annual compounding. The Problem with YTM spreads[edit] <span>Coupon Paying bonds are essentially portfolios of Zero Coupon Bond components and the Yield to Maturity of such instruments can be thought of as being a complex blend of the component Zero Coupon bond yields. It therefore can be observed that, for example, in a positively sloped Yield Curve environment and comparing two bonds with the same cash flow dates and maturity, a higher coupon bond will offer a lower YTM than a low coupon bond. (The low coupon bond has cash flows more heavily influenced by a proportionally greater long term component). Thus two fairly and correctly priced corporate bonds from the same borrower and having the same cash flow dates and maturity may well have significantly different Yields to Maturity. It
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to maturity - Wikipedia, the free encyclopedia
nternal rate of return (IRR, overall interest rate) earned by an investor who buys the bond today at the market price, assuming that the bond will be held until maturity, and that all coupon and principal payments will be made on schedule.[1] <span>Yield to maturity is simply the discount rate at which the sum of all future cash flows from the bond (coupons and principal) is equal to the price of the bond. The YTM is often given in terms of Annual Percentage Rate (A.P.R.), but more usually market convention is followed. In a number of major markets (such as gilts) the convention is to quot
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to maturity - Wikipedia, the free encyclopedia
usually quoted without making any allowance for tax paid by the investor on the return, and is then known as "gross redemption yield". It also does not make any allowance for the dealing costs incurred by the purchaser (or seller). <span>Coupon rate vs. YTM[edit] If a bond's coupon rate is less than its YTM, then the bond is selling at a discount.If a bond's coupon rate is more than its YTM, then the bond is selling at a premium.If a bond's coupon rate is equal to its YTM, then the bond is selling at par. Variants of yield to maturity[edit] As some bonds have different characteristics, there are some variants of YTM: Yield to call: when a bond is callable (can be repurchased by the issuer
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to maturity - Wikipedia, the free encyclopedia
bond's coupon rate is less than its YTM, then the bond is selling at a discount.If a bond's coupon rate is more than its YTM, then the bond is selling at a premium.If a bond's coupon rate is equal to its YTM, then the bond is selling at par. <span>Variants of yield to maturity[edit] As some bonds have different characteristics, there are some variants of YTM: Yield to call: when a bond is callable (can be repurchased by the issuer before the maturity), the market looks also to the Yield to call, which is the same calculation of the YTM, but assumes that the bond will be called, so the cashflow is shortened. Yield to put: same as yield to call, but when the bond holder has the option to sell the bond back to the issuer at a fixed price on specified date. Yield to worst: when a bond is callable, puttable, exchangeable, or has other features, the yield to worst is the lowest yield of yield to maturity, yield to call, yield to put, and others. Formula for yield to maturity for zero-coupon bonds[edit] Example 1[edit] Consider a 30-year zero-coupon bond with a face value of $100. If the bond is priced at an annual YTM of 10%, i
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to Maturity
the way until maturity while reinvesting all coupon payments at the bond yield. It should not be confused with holding period return, as the two often differ. Yield to maturity is generally given in terms of Annual Percentage Rate (APR), and <span>it is an estimation of future return, as the rate at which coupon payments can be reinvested at is unknown. However, for zero coupon bonds, the yield to maturity and the rate of return are equivalent since there are no coupon payments to reinvest. Another way of putting it is that the yield to
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to Maturity
ng period return, as the two often differ. Yield to maturity is generally given in terms of Annual Percentage Rate (APR), and it is an estimation of future return, as the rate at which coupon payments can be reinvested at is unknown. However, <span>for zero coupon bonds, the yield to maturity and the rate of return are equivalent since there are no coupon payments to reinvest. Another way of putting it is that the yield to maturity is the rate of return that makes the present value (PV) of the cash flow generated by the bond equal to the price. Yield to maturi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to Maturity
e rate at which coupon payments can be reinvested at is unknown. However, for zero coupon bonds, the yield to maturity and the rate of return are equivalent since there are no coupon payments to reinvest. Another way of putting it is that the <span>yield to maturity is the rate of return that makes the present value (PV) of the cash flow generated by the bond equal to the price. Yield to maturity is widely used by investors as a way to compare bonds with different face values, coupon payments, and time till maturity. Yield to Maturity Terminology Face Value, a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield to Maturity
value (PV) of the cash flow generated by the bond equal to the price. Yield to maturity is widely used by investors as a way to compare bonds with different face values, coupon payments, and time till maturity. Yield to Maturity Terminology <span>Face Value, also known as the "par value", is the amount a bond holder will be paid when it matures. For example, a zero coupon bond with a $1000 face value and one year to maturity means that in exactly one year, the bond holder is entitled to $1000 from the issuer. Coupon rate is th
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
the bond at price ,hold the bond until maturity, andredeem the bond at par. Coupon yield[edit] The coupon yield is simply the coupon payment as a percentage of the face value . Coupon yield is also called nominal yield. Current yield[edit] <span>The current yield is simply the coupon payment as a percentage of the (current) bond price . Relationship[edit] The concept of current yield is closely related to other bond concepts, including yield to maturity, and coupon yield. The relationship between yield to maturity and t
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
ices are often quoted in terms of YTM. To achieve a return equal to YTM, i.e. where it is the required return on the bond, the bond owner must: buy the bond at price ,hold the bond until maturity, andredeem the bond at par. Coupon yield[edit] <span>The coupon yield is simply the coupon payment as a percentage of the face value . Coupon yield is also called nominal yield. Current yield[edit] The current yield is simply the coupon payment as a percentage of the (current) bond price . Relationship[edit] The concept of current yield is closely related to o
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
y of the TED spread TED spread (in red) and components during the Financial crisis of 2007–08 The TED spread is the difference between the interest rates on interbank loans and on short-term U.S. government debt ("T-bills"). <span>TED is an acronym formed from T-Bill and ED, the ticker symbol for the Eurodollar futures contract. Initially, the TED spread was the difference between the interest rates for three-month U.S. Treasuries contracts and the three-month Eurodollars contract as represented by the London In
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
From Wikipedia, the free encyclopedia Jump to: navigation, search Long term history of the TED spread TED spread (in red) and components during the Financial crisis of 2007–08 <span>The TED spread is the difference between the interest rates on interbank loans and on short-term U.S. government debt ("T-bills"). TED is an acronym formed from T-Bill and ED, the ticker symbol for the Eurodollar futures contract. Initially, the TED spread was the difference between the interest rates for three-mo
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
ge dropped T-bill futures after the 1987 crash,[1] the TED spread is now calculated as the difference between the three-month LIBOR and the three-month T-bill interest rate. The size of the spread is usually denominated in basis points (bps). <span>For example, if the T-bill rate is 5.10% and ED trades at 5.50%, the TED spread is 40 bps. The TED spread fluctuates over time but generally has remained within the range of 10 and 50 bps (0.1% and 0.5%) except in times of financial crisis. A rising TED spread often presages a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
f financial crisis. A rising TED spread often presages a downturn in the U.S. stock market, as it indicates that liquidity is being withdrawn. Contents 1 Indicator2 Historical levels3 See also4 References5 External links Indicator[edit] <span>The TED spread is an indicator of perceived credit risk in the general economy,[2] since T-bills are considered risk-free while LIBOR reflects the credit risk of lending to commercial banks. An increase in the TED spread is a sign that lenders believe the risk of default on interbank loans (also known as counterparty risk) is increasing. Interbank lenders, therefore, deman
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
ate of interest, or accept lower returns on safe investments such as T-bills. When the risk of bank defaults is considered to be decreasing, the TED spread decreases.[3] Historical levels[edit] This section requires expansion. (November 2008) <span>The long term average of the TED has been 30 basis points with a maximum of 50 bps. During 2007, the subprime mortgage crisis ballooned the TED spread to a region of 150–200 bps. On September 17, 2008, the TED spread exceeded 300 bps, breaking the previous record set after the Black Monday crash of 1987.[4] Some higher readings for the spread were due to inability to obtain accurate LIBOR rates in the absence of a liquid unsecured lending market.[5] On October 10, 2008, the TED spread reached another new high of 457 basis points. In October 2013, due to worries regarding a potential default on US debt, the 1 month TED went negative for the first time since it started being tracked.[6][7] See also[edit] LIBOR-OIS spreadOvernight indexed swapTreasury BillTreasury security References[edit] ^ http://www.atimes.com/atimes/Global_Economy/LK25Dj01.html^ Bloomberg.com F
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
. For example, if the T-bill rate is 5.10% and ED trades at 5.50%, the TED spread is 40 bps. The TED spread fluctuates over time but generally has remained within the range of 10 and 50 bps (0.1% and 0.5%) except in times of financial crisis. <span>A rising TED spread often presages a downturn in the U.S. stock market, as it indicates that liquidity is being withdrawn. Contents 1 Indicator2 Historical levels3 See also4 References5 External links Indicator[edit] The TED spread is an indicator of perceived credit risk in the general economy,[2] since
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
I-spread - Wikipedia, the free encyclopedia
enwiki:resourceloader:filter:minify-css:7:3904d24a08aa08f6a68dc338f9be277e */ I-spread From Wikipedia, the free encyclopedia Jump to: navigation, search <span>The Interpolated Spread or I-spread or ISPRD is the difference between the yield to maturity of the bond and the linearly interpolated yield to the same maturity on an appropriate reference curve.[1] See also[edit] Option-adjusted spreadZ-spread References[edit] ^ Credit Spreads Explained vte Bond market BondDebentureFixed income Types of bonds by issuer Agency bondCor
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
yield curve the sum of their values will tend to overestimate the market price of the MBS. The parallel shift, which, if applied to the yield curve makes the NPV of the anticipated receipts equal to the market price is the Yield curve spread. <span>The Z-spread of a bond is the number of basis points one needs to add to the Treasury spot rates yield curve, so that the NPV of the bond cash flows (using the adjusted yield curve) equals the market price of the bond (after accounting for accrued interest). The spread is calculated iteratively and improves the accuracy of the value calculation as it uses the entire yield curve to value the cash flows. If you calculate the present value of a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
onal factors such as liquidity and credit risk. The Z-spread quantifies the impact of these additional factors. It is the spread you need to add to the curve you are discounting with in order to generate a price that matches the market price. <span>Conventionally, the zero rates are determined from the Treasury curve, with semi-annual compounding. The Problem with YTM spreads[edit] Coupon Paying bonds are essentially portfolios of Zero Coupon Bond components and the Yield to Maturity of such instruments can be thought of as being
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
usted yield curve) equals the market price of the bond (after accounting for accrued interest). The spread is calculated iteratively and improves the accuracy of the value calculation as it uses the entire yield curve to value the cash flows. <span>If you calculate the present value of all future cash flows for a bond using prevailing spot rates, you may discover that the price you calculate is greater than the price observed in the market. This difference arises because the market price incorporates additional factors such as liquidity and credit risk. The Z-spread quantifies the impact of these additional factors. It is the spread you need to add to the curve you are discounting with in order to generate a price that matches the market price. Conventionally, the zero rates are determined from the Treasury curve, with semi-annual compounding. The Problem with YTM spreads[edit] Coupon Paying bonds are essentially portfolios of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
age-backed securities, a model of typical repayment rates tends to be given; for example, the PSA formula for a particular Fannie Mae MBS might equate a particular group of mortgages to an 8 year amortizing bond with a 5% mortality per annum. <span>This gives a single series of nominal cash flows (like a riskless bond). If these payments are discounted to net present value with a static treasury yield curve the sum of their values will tend to overestimate the market price of the MBS. The parallel shift, which, if applied to the yield curve makes the NPV of the anticipated receipts equal to the market price is the Yield curve spread. The Z-spread of a bond is the number of basis points one needs to add to the Treasury spot rates yield curve, so that the NPV of the bond cash flows (using the adjusted yield curve) equa
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
bond. The market's anticipation of falling interest rates causes such incidents. Negative liquidity premiums can also exist if long-term investors dominate the market, but the prevailing view is that a positive liquidity premium dominates, so <span>only the anticipation of falling interest rates will cause an inverted yield curve. Strongly inverted yield curves have historically preceded economic depressions. The shape of the yield curve is influenced by supply and demand: for instance, if there is a large demand
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
g in a credit bubble. Theory[edit] There are three main economic theories attempting to explain how yields vary with maturity. Two of the theories are extreme positions, while the third attempts to find a middle ground between the former two. <span>Market expectations (pure expectations) hypothesis[edit] Main article: expectation hypothesis This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants' expectations of future interest rates. Using this, future rates, along with the assumption that arbitrage opportunities will be minimal in future markets, and that future rates are unbiased estimates of forthcoming spot rates, is enough information to construct a complete expected yield curve. For example, if investors have an expectation of what 1-year interest rates will be next year, the 2-year interest rate can be calculated as the compounding of this year's interest rate by next year's interest rate. More generally, rates on a long-term instrument are equal to the geometric mean of the yield on a series of short-term instruments. This theory perfectly explains the observation that yields usually move together. However, it fails to explain the persistence in the shape of the yield curve. Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk Liquidity premium theory[edit] The Liquidity Premium Theory is an offshoot of the Pure Expectations Theory. The Liquidity Premium Theory asserts that long-term interest rates not only re
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
stence in the shape of the yield curve. Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk <span>Liquidity premium theory[edit] The Liquidity Premium Theory is an offshoot of the Pure Expectations Theory. The Liquidity Premium Theory asserts that long-term interest rates not only reflect investors’ assumptions about future interest rates but also include a premium for holding long-term bonds (investors prefer short term bonds to long term bonds), called the term premium or the liquidity premium. This premium compensates investors for the added risk of having their money tied up for a longer period, including the greater price uncertainty. Because of the term premium, long-term bond yields tend to be higher than short-term yields, and the yield curve slopes upward. Long term yields are also higher not just because of the liquidity premium, but also because of the risk premium added by the risk of default from holding a security over the long term. The market expectations hypothesis is combined with the liquidity premium theory: Where is the risk premium associated with an year bond. Market segmentation theory[edit] This theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result,
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
because of the risk premium added by the risk of default from holding a security over the long term. The market expectations hypothesis is combined with the liquidity premium theory: Where is the risk premium associated with an year bond. <span>Market segmentation theory[edit] This theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result, the supply and demand in the markets for short-term and long-term instruments is determined largely independently. Prospective investors decide in advance whether they need short-term or long-term instruments. If investors prefer their portfolio to be liquid, they will prefer short-term instruments to long-term instruments. Therefore, the market for short-term instruments will receive a higher demand. Higher demand for the instrument implies higher prices and lower yield. This explains the stylized fact that short-term yields are usually lower than long-term yields. This theory explains the predominance of the normal yield curve shape. However, because the supply and demand of the two markets are independent, this theory fails to explain the observed fact that yields tend to move together (i.e., upward and downward shifts in the curve). Preferred habitat theory[edit] The preferred habitat theory is another guide of the liquidity premium theory, and states that in addition to interest rate expectations, investors have di
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
ance of the normal yield curve shape. However, because the supply and demand of the two markets are independent, this theory fails to explain the observed fact that yields tend to move together (i.e., upward and downward shifts in the curve). <span>Preferred habitat theory[edit] The preferred habitat theory is another guide of the liquidity premium theory, and states that in addition to interest rate expectations, investors have distinct investment horizons and require a meaningful premium to buy bonds with maturities outside their "preferred" maturity, or habitat. Proponents of this theory believe that short-term investors are more prevalent in the fixed-income market, and therefore longer-term rates tend to be higher than short-term rates, for the most part, but short-term rates can be higher than long-term rates occasionally. This theory is consistent with both the persistence of the normal yield curve shape and the tendency of the yield curve to shift up and down while retaining its shape. Historical development of yield curve theory[edit] On 15 August 1971, U.S. President Richard Nixon announced that the U.S. dollar would no longer be based on the gold standard, thereby e
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
00Swap2y6.01253Swap3y6.10823Swap4y6.16Swap5y6.22Swap7y6.32Swap10y6.42Swap15y6.56Swap20y6.56Swap30y6.56 A list of standard instruments used to build a money market yield curve. The data is for lending in US dollar, taken from October 6, 1997 <span>The usual representation of the yield curve is a function P, defined on all future times t, such that P(t) represents the value today of receiving one unit of currency t years in the future. If P is defined for all future t then we can easily recover the yield (i.e. the annualized interest rate) for borrowing money for that period of time via the formula The significant difficulty in defining a yield curve therefore is to determine the function P(t). P is called the discount factor function. Yield curves are built from either prices available in the bond market or the money market. Whilst the yield curves built from the bond market use prices only from a specific class of bo
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itThe usual representation of the yield curve is a function P, defined on all future times t, such that P(t) represents the value today of receiving one unit of currency t years in the future. If P is defined for all future t then we can easily recover the yield (i.e. the annualized interest rate) for borrowing money for that period of time via the formula The significant dif
Original toplevel document
Yield curve - Wikipedia, the free encyclopedia00Swap2y6.01253Swap3y6.10823Swap4y6.16Swap5y6.22Swap7y6.32Swap10y6.42Swap15y6.56Swap20y6.56Swap30y6.56 A list of standard instruments used to build a money market yield curve. The data is for lending in US dollar, taken from October 6, 1997 <span>The usual representation of the yield curve is a function P, defined on all future times t, such that P(t) represents the value today of receiving one unit of currency t years in the future. If P is defined for all future t then we can easily recover the yield (i.e. the annualized interest rate) for borrowing money for that period of time via the formula The significant difficulty in defining a yield curve therefore is to determine the function P(t). P is called the discount factor function. Yield curves are built from either prices available in the bond market or the money market. Whilst the yield curves built from the bond market use prices only from a specific class of bo
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
on. Yield curves are built from either prices available in the bond market or the money market. Whilst the yield curves built from the bond market use prices only from a specific class of bonds (for instance bonds issued by the UK government) <span>yield curves built from the money market use prices of "cash" from today's LIBOR rates, which determine the "short end" of the curve i.e. for t ≤ 3m, futures which determine the midsection of the curve (3m ≤ t ≤ 15m) and interest rate swaps which determine the "long end" (1y ≤ t ≤ 60y). The example given in the table at the right is known as a LIBOR curve because it is constructed using either LIBOR rates or swap rates. A LIBOR curve is the most widely used interest rat
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
orward interest rates, zero coupon bond prices, or zero coupon bond yieldsLocal regression using kernelsLinear programming In the money market practitioners might use different techniques to solve for different areas of the curve. For example <span>at the short end of the curve, where there are few cashflows, the first few elements of P may be found by bootstrapping from one to the next. At the long end, a regression technique with a cost function that values smoothness might be used. How the yield curve affects bond prices[edit] There is a time dimension to the analysis
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
TED spread - Wikipedia, the free encyclopedia
for three-month U.S. Treasuries contracts and the three-month Eurodollars contract as represented by the London Interbank Offered Rate (LIBOR). However, since the Chicago Mercantile Exchange dropped T-bill futures after the 1987 crash,[1] the <span>TED spread is now calculated as the difference between the three-month LIBOR and the three-month T-bill interest rate. The size of the spread is usually denominated in basis points (bps). For example, if the T-bill rate is 5.10% and ED trades at 5.50%, the TED spread is 40 bps. The TED spread fluctuates
Flashcard 149623953
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTED spread is now calculated as the difference between the three-month LIBOR and the three-month T-bill interest rate.
Original toplevel document
TED spread - Wikipedia, the free encyclopediafor three-month U.S. Treasuries contracts and the three-month Eurodollars contract as represented by the London Interbank Offered Rate (LIBOR). However, since the Chicago Mercantile Exchange dropped T-bill futures after the 1987 crash,[1] the <span>TED spread is now calculated as the difference between the three-month LIBOR and the three-month T-bill interest rate. The size of the spread is usually denominated in basis points (bps). For example, if the T-bill rate is 5.10% and ED trades at 5.50%, the TED spread is 40 bps. The TED spread fluctuates
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
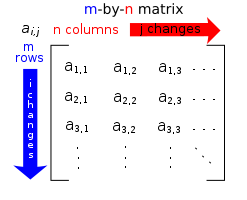
Matrix (mathematics) - Wikipedia, the free encyclopedia
Matrix (mathematics) From Wikipedia, the free encyclopedia Jump to: navigation, search "Matrix theory" redirects here. For the physics topic, see Matrix string theory. <span>Each element of a matrix is often denoted by a variable with two subscripts. For instance, a2,1 represents the element at the second row and first column of a matrix A. In mathematics, a matrix (plural matrices) is a rectangular array[1] of numbers, symbols, or expressions, arranged in rows and columns.[2][3] The individual items in a matrix are called
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
ivate borrowing is at a premium above government borrowing, of similar maturity is a measure of risk tolerance of the lenders. For the U. S. market, a common benchmark for such a spread is given by the so-called TED spread. In either case the <span>available market data provides a matrix A of cash flows, each row representing a particular financial instrument and each column representing a point in time. The (i,j)-th element of the matrix represents the amount that instrument i will pay out on day j. Let the vector F represent today's prices of the instrument (so that the i-th instrument has value F(i)), then by definition of our discount factor function P we should have that F = AP (this is a matrix multiplication). Actually, noise in the financial markets means it is not possible to find a P that solves this equation exactly, and our goal becomes to find a vector P such that where is as small a vector as possible (where the size of a vector might be measured by taking its norm, for example). Note that even if we can solve this equation, we will only have determined P(t) for those t which have a c
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
by bootstrapping from one to the next. At the long end, a regression technique with a cost function that values smoothness might be used. How the yield curve affects bond prices[edit] There is a time dimension to the analysis of bond values. <span>A 10-year bond at purchase becomes a 9-year bond a year later, and the year after it becomes an 8-year bond, etc. Each year the bond moves incrementally closer to maturity, resulting in lower volatility and shorter duration and demanding a lower interest rate when the yield curve is rising. Since falling rates create increasing prices, the value of a bond initially will rise as the lower rates of the shorter maturity become its new market rate. Because a bond is always anchored by its final maturity, the price at some point must change direction and fall to par value at redemption. A bond's market value at different times in its life can be calculated. When the yield curve is steep, the bond is predicted to have a large capital gain in the first years before fallin
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
ty become its new market rate. Because a bond is always anchored by its final maturity, the price at some point must change direction and fall to par value at redemption. A bond's market value at different times in its life can be calculated. <span>When the yield curve is steep, the bond is predicted to have a large capital gain in the first years before falling in price later. When the yield curve is flat, the capital gain is predicted to be much less, and there is little variability in the bond's total returns over time. Rising (or falling) interest rates rar
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
and fall to par value at redemption. A bond's market value at different times in its life can be calculated. When the yield curve is steep, the bond is predicted to have a large capital gain in the first years before falling in price later. W<span>hen the yield curve is flat, the capital gain is predicted to be much less, and there is little variability in the bond's total returns over time. Rising (or falling) interest rates rarely rise by the same amount all along the yield curve—the curve rarely moves up in parallel. Because longer-term bonds have a larger duration, a ris
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Yield curve - Wikipedia, the free encyclopedia
pital gain is predicted to be much less, and there is little variability in the bond's total returns over time. Rising (or falling) interest rates rarely rise by the same amount all along the yield curve—the curve rarely moves up in parallel. <span>Because longer-term bonds have a larger duration, a rise in rates will cause a larger capital loss for them, than for short-term bonds. But almost always, the long maturity's rate will change much less, flattening the yield curve. The greater change in rates at the short end will offset to some extent the advantage provided by the shorter bond's lower duration. The yearly 'total return' from the bond is a) the sum of the coupon's yield plus b) the capital gain from the changing valuation as it slides down the yield curve and c) any capital gain
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
> current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield Price sensitivity[edit] Main articles: Bond duration and Bond convexity <span>The sensitivity of a bond's market price to interest rate (i.e. yield) movements is measured by its duration, and, additionally, by its convexity. Duration is a linear measure of how the price of a bond changes in response to interest rate changes. It is approximately equal to the percentage change in price for a given change in yi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
s simply the coupon payment as a percentage of the face value . Coupon yield is also called nominal yield. Current yield[edit] The current yield is simply the coupon payment as a percentage of the (current) bond price . Relationship[edit] <span>The concept of current yield is closely related to other bond concepts, including yield to maturity, and coupon yield. The relationship between yield to maturity and the coupon rate is as follows: When a bond sells at a discount, YTM > current yield > coupon yield.When a bond sells at a premium, coupon yield > current yield > YTM.When a bond sells at par, YTM = current yield = coupon yield Price sensitivity[edit] Main articles: Bond duration and Bond convexity The sensitivity of a bond's market price to interest rate (i.e. yield) movements is measured by its duration, and,
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
nsitivity of a bond's market price to interest rate (i.e. yield) movements is measured by its duration, and, additionally, by its convexity. Duration is a linear measure of how the price of a bond changes in response to interest rate changes. <span>It is approximately equal to the percentage change in price for a given change in yield, and may be thought of as the elasticity of the bond's price with respect to discount rates. For example, for small interest rate changes, the duration is the approximate percentage by which the value of the bond will fall for a 1% per annum increase in market interest rate. S
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
of the bond's price with respect to discount rates. For example, for small interest rate changes, the duration is the approximate percentage by which the value of the bond will fall for a 1% per annum increase in market interest rate. So the <span>market price of a 17-year bond with a duration of 7 would fall about 7% if the market interest rate (or more precisely the corresponding force of interest) increased by 1% per annum. Convexity is a measure of the "curvature" of price changes. It is needed because the price is not a linear function of the discount rate, but rather a convex function of the di
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond valuation - Wikipedia, the free encyclopedia
rce of interest) increased by 1% per annum. Convexity is a measure of the "curvature" of price changes. It is needed because the price is not a linear function of the discount rate, but rather a convex function of the discount rate. <span>Specifically, duration can be formulated as the first derivative of the price with respect to the interest rate, and convexity as the second derivative (see: Bond duration closed-form formula; Bond convexity closed-form formula; Taylor series). Continuing the above example, for a more accurate estimate of sensitivity, the convexity scor
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Elasticity (economics) - Wikipedia, the free encyclopedia
nclear to readers. Please help us clarify the article; suggestions may be found on the talk page. (December 2010) In economics, elasticity is the measurement of how responsive an economic variable is to a change in another. For example: "<span>If I lower the price of my product, how much more will I sell?""If I raise the price of one good, how will that affect sales of this other good?""If we learn that a resource is becoming scarce, will people scramble to acquire it
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Z-spread - Wikipedia, the free encyclopedia
y equal the bond's price. If they do, then you have found the Z-spread, if not, you have to go back to the drawing board and use a new spread until the present value of those cash flows equals the bond's price. The Advantage of Z-Spread[edit] <span>As the Z-Spread is not dependent upon only one point on the Yield Curve and takes account of all of the relevant term-structure, the distortions of Yield-to-Maturity spreads outlined above are eliminated. It is then a measure of Credit Spread without the distortions of YTM. It is widely used in the CDS and other markets by non bond traders who want a fair reading of Credit Spread undistorted by the complexities of individual bonds. Benchmark for CDS Basis[e
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Bond duration - Wikipedia, the free encyclopedia
Dollar duration, DV01 6.1 Application to Value-at-Risk (VaR) 7 Embedded options and effective duration8 Spread duration9 Average duration10 Convexity11 See also12 Notes13 References14 Further reading15 External links Macaulay duration[edit] <span>Macaulay duration, named for Frederick Macaulay who introduced the concept, is the weighted average maturity of cash flows. Consider some set of fixed cash flows. The present value of these cash flows is: Macaulay duration is defined as:[1][2][3] [4] (1) where: indexes the cash flows, is the present value of the th cash payment from an asset, is the time in years until the th payment will be received, is the present value of all future cash payments from the asset. In the second expression the fractional term is the ratio of the cash flow to the total PV. These terms add to 1.0 and serve as weights for a weighted average. Thus the overall expressi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Eurasian eagle-owl - Wikipedia, the free encyclopedia
ientific classificationKingdom:AnimaliaPhylum:ChordataClass:AvesOrder:StrigiformesFamily:StrigidaeGenus:BuboSpecies:B. buboBinomial nameBubo bubo (Linnaeus, 1758)Range of Eurasian Eagle-OwlSynonyms Bubo ignavus Forster, 1817Bubo maximus [2] <span>The Eurasian eagle-owl (Bubo bubo) is a species of eagle-owl resident in much of Eurasia. It is sometimes called the European eagle-owl and is, in Europe, where it is the only member of its genus besides the snowy owl (B. scandiacus), occasionally abbreviated to just eagle-ow
 as a percentage of the (current) bond price
as a percentage of the (current) bond price 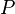 .
.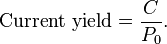
 as a percentage of the face value
as a percentage of the face value 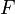 .
.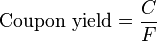
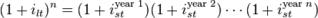
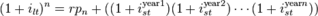
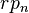 is the risk premium associated with an
is the risk premium associated with an 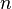 year bond.
year bond.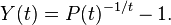
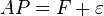
 is as small a vector as possible
is as small a vector as possible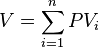
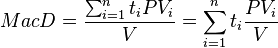
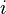 indexes the cash flows,
indexes the cash flows,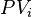 is the
is the 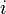 th cash payment from an
th cash payment from an 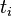 is the time in years until the
is the time in years until the 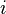 th payment will be received,
th payment will be received,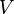 is the present value of all future cash payments from the asset.
is the present value of all future cash payments from the asset.