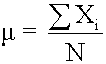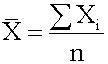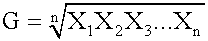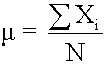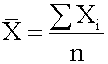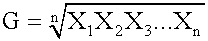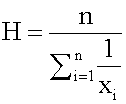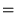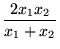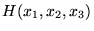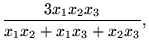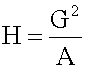Edited, memorised or added to reading queue
on 02-Apr-2016 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itA statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
Flashcard 1332009897228
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA statistic is defined as a numerical quantity (such as the mean) calculated in a sample.
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
Flashcard 1332011470092
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA statistic is defined as a numerical quantity (such as the mean) calculated in a sample.
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itge returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that <span>we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters.<span><body><html>
Original toplevel document
Subject 1. The Nature of StatisticsEstimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span>A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to numerical data such as a company's earnings per share or average returns over the past five years. Statistics can also refer to the process of collecting, organizing, presenting, analyzing, and interpreting numerical data for the purpose of making decisions. Note that we will always know the exact composition of our sample, and by definition, we will always know the values within our sample. Ascertaining this information is the purpose of samples. Sample statistics will always be known, and can be used to estimate unknown population parameters. Hint: One way to easily remember these terms is to recall that "population" and "parameter" both start with a "p," and "sample" and "statisti
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itHint: Remember the order of the different scales by remembering NOIR (the French word for black); the first letter of each word in the scale is indicated by the letters in the word NOIR.
Original toplevel document
Subject 2. Measurement Scalesey. Both examples can be measured on a zero scale, where zero represents no return, or in the case of money, no money. Note that as you move down through this list, the measurement scales get stronger. <span>Hint: Remember the order of the different scales by remembering NOIR (the French word for black); the first letter of each word in the scale is indicated by the letters in the word NOIR. Before we move on, here's a quick exercise to make sure that you understand the different measurement scales. In each case, identify whether you think the data is nominal, ordinal, inter
Flashcard 1332018023692
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe order of the different scales is NOIR (the French word for black)
Original toplevel document
Subject 2. Measurement Scalesey. Both examples can be measured on a zero scale, where zero represents no return, or in the case of money, no money. Note that as you move down through this list, the measurement scales get stronger. <span>Hint: Remember the order of the different scales by remembering NOIR (the French word for black); the first letter of each word in the scale is indicated by the letters in the word NOIR. Before we move on, here's a quick exercise to make sure that you understand the different measurement scales. In each case, identify whether you think the data is nominal, ordinal, inter
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itA parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in s
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
Flashcard 1332022742284
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA parameter is a numerical quantity measuring some aspect of a population of scores.
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
Flashcard 1332024315148
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA parameter is a numerical quantity measuring some aspect of a population of scores.
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itpopulation of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. <span>Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a populati
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. <span>Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. <span><body><html>
Original toplevel document
Subject 1. The Nature of Statisticsve values associated with them, such as the average of all values in a sample and the average of all population values. Values from a population are called parameters, and values from a sample are called statistics. <span>A parameter is a numerical quantity measuring some aspect of a population of scores. The mean, for example, is a measure of central tendency. Greek letters are used to designate parameters. Parameters are rarely known and are usually estimated by statistics computed in samples. Populations can have many parameters, but investment analysts are usually only concerned with a few, such as the mean return or the standard deviation of returns. Estimates of these parameters taken from a sample are called statistics. Much of the field of statistics is devoted to drawing inferences from a sample concerning the value of a population parameter. A statistic is defined as a numerical quantity (such as the mean) calculated in a sample. It has two different meanings. Most commonly, statistics refers to
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itInterval Scale Interval scales rank measurements and ensure that the intervals between the rankings are equal. Scale values can be added and subtracted from each other. For example, if anxiety was measured on an interval scale, a difference between a score of 10 and a score of 11 would represent the same difference in anxiety as the difference between a score of 50 and a score of 51. Interval scales do not have a "true" zero point. Therefore, it is not possible to make statements about how many times higher one score is than another. For the anxiety example, it would not be valid to say that a person with a score o
Original toplevel document
Subject 2. Measurement Scalesno "true" zero point for ordinal scales, since the zero point is chosen arbitrarily. The lowest point on the rating scale in the example was arbitrarily chosen to be 1. It could just as well have been 0 or -5. <span>Interval Scale Interval scales rank measurements and ensure that the intervals between the rankings are equal. Scale values can be added and subtracted from each other. For example, if anxiety was measured on an interval scale, a difference between a score of 10 and a score of 11 would represent the same difference in anxiety as the difference between a score of 50 and a score of 51. Interval scales do not have a "true" zero point. Therefore, it is not possible to make statements about how many times higher one score is than another. For the anxiety example, it would not be valid to say that a person with a score of 30 was twice as anxious as a person with a score of 15. True interval measurement is somewhere between rare and nonexistent in the behavioral sciences. No interval scales measuring anxiety, such as the one described in the example, actually exist. A good example of an interval scale is the Fahrenheit measure of temperature. Equal differences on this scale represent equal differences in temperature, but a temperature of 30°F is not twice as warm as one of 15°F. Ratio Scale Ratio scales are like interval scales except that they have true zero points. This is the strongest measurement scale. In addition to permitting ranking and a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open its twice as anxious as a person with a score of 15. True interval measurement is somewhere between rare and nonexistent in the behavioral sciences. No interval scales measuring anxiety, such as the one described in the example, actually exist. <span>A good example of an interval scale is the Fahrenheit measure of temperature. Equal differences on this scale represent equal differences in temperature, but a temperature of 30°F is not twice as warm as one of 15°F. <span><body><html>
Original toplevel document
Subject 2. Measurement Scalesno "true" zero point for ordinal scales, since the zero point is chosen arbitrarily. The lowest point on the rating scale in the example was arbitrarily chosen to be 1. It could just as well have been 0 or -5. <span>Interval Scale Interval scales rank measurements and ensure that the intervals between the rankings are equal. Scale values can be added and subtracted from each other. For example, if anxiety was measured on an interval scale, a difference between a score of 10 and a score of 11 would represent the same difference in anxiety as the difference between a score of 50 and a score of 51. Interval scales do not have a "true" zero point. Therefore, it is not possible to make statements about how many times higher one score is than another. For the anxiety example, it would not be valid to say that a person with a score of 30 was twice as anxious as a person with a score of 15. True interval measurement is somewhere between rare and nonexistent in the behavioral sciences. No interval scales measuring anxiety, such as the one described in the example, actually exist. A good example of an interval scale is the Fahrenheit measure of temperature. Equal differences on this scale represent equal differences in temperature, but a temperature of 30°F is not twice as warm as one of 15°F. Ratio Scale Ratio scales are like interval scales except that they have true zero points. This is the strongest measurement scale. In addition to permitting ranking and a
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
Measures of central tendency specify where data are centered. They attempt to use a typical value to represent all the observations in the data set. Population Mean The population mean is the average for a finite population. It is unique; a given population has only one mean.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
Measures of central tendency specify where data are centered. They attempt to use a typical value to represent all the observations in the data set. Population Mean The population mean is the average for a finite population. It is unique; a given population has only one mean. where: N = the number of observations in the entire population X i = the ith observation ΣX i = add up X i , where i is from 0 to N Sample Mean The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
13; where: N = the number of observations in the entire population X i = the ith observation ΣX i = add up X i , where i is from 0 to N <span>Sample Mean The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itArithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1332040830220
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe arithmetic mean is what is commonly called the average.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itArithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mea
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1332043451660
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe population mean and sample mean are both examples of the arithmetic mean.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itdata set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. <span>This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itthe arithmetic mean is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
Flashcard 1332048432396
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itthe arithmetic mean is the most widely used measure of central tendency.
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. <span>The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data se
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itefer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. <span>All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is th
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itd ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. <span>The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determi
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open iteasure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. <span>The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span><body><html>
Original toplevel document
Subject 4. Measures of Center Tendency; The sample mean is the average for a sample. It is a statistic and is used to estimate the population mean. where n = the number of observations in the sample <span>Arithmetic Mean The arithmetic mean is what is commonly called the average. The population mean and sample mean are both examples of the arithmetic mean. If the data set encompasses an entire population, the arithmetic mean is called a population mean. If the data set includes a sample of values taken from a population, the arithmetic mean is called a sample mean. This is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores. It is used to measure the prospective (expected future) performance (return) of an investment over a number of periods. All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean. All data values are considered and included in the arithmetic mean computation. A data set has only one arithmetic mean. This indicates that the mean is unique. The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The arithmetic mean has the following disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). Geometric Mean The geometric mean has three important properties: It exists only if all the observations are gre
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
owing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itGeometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not
Original toplevel document
Subject 4. Measures of Center Tendencyowing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itvations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. <span>It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometr
Original toplevel document
Subject 4. Measures of Center Tendencyowing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itor negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. <span>It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. <span><body><html>
Original toplevel document
Subject 4. Measures of Center Tendencyowing disadvantages: The mean can be affected by extremes, that is, unusually large or small values. The mean cannot be determined for an open-ended data set (i.e., n is unknown). <span>Geometric Mean The geometric mean has three important properties: It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative. If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value. It is always less than the arithmetic mean if values in the data set are not equal. It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to eac
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. <span>Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to each value. Notice that the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The assets are weighted on their market values relative to the market value of the portfolio. When we take a weighted average of forward-looking data, the weighted mean is calledexpected value. Example A year ago, a certain share had a price of $6. Six months ago, the same share had a price of $6.20. The share is now trading at $7.50. Because the most recent price is the most reliable, we decide to attach more relevance to this value. So, suppose we decide to "weight" the prices in the ratio 1:2:4, so that the current share price is twice as important as the price from six months ago, which in turn is twice as important as the price from last year. The weighted mean would then be: (1 x 6 + 2 x 6.2 + 4 x 7.5) / (1 + 2 + 4) = $6.91. If we calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median doe
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itWeighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to each value. Notice that the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The assets are weighted on their market values relative to the market value of the portfolio. When we take a weighted average of forward-looking data, the weighted mean is calledexpected value. Example A year ago, a certain share had a price of $6. Six months ago, the same share had a price of $6.20. The share is now trading at $7.50. Because the most recent
Original toplevel document
Subject 4. Measures of Center Tendencymean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean. <span>Weighted Mean The weighted mean is computed by weighting each observed value according to its importance. In contrast, the arithmetic mean assigns equal weight to each value. Notice that the return of a portfolio is the weighted mean of the returns of individual assets in the portfolio. The assets are weighted on their market values relative to the market value of the portfolio. When we take a weighted average of forward-looking data, the weighted mean is calledexpected value. Example A year ago, a certain share had a price of $6. Six months ago, the same share had a price of $6.20. The share is now trading at $7.50. Because the most recent price is the most reliable, we decide to attach more relevance to this value. So, suppose we decide to "weight" the prices in the ratio 1:2:4, so that the current share price is twice as important as the price from six months ago, which in turn is twice as important as the price from last year. The weighted mean would then be: (1 x 6 + 2 x 6.2 + 4 x 7.5) / (1 + 2 + 4) = $6.91. If we calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median doe
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
we calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. <span>Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itMedian In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the m
Original toplevel document
Subject 4. Measures of Center Tendencywe calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. <span>Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itin order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. <span>To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more infor
Original toplevel document
Subject 4. Measures of Center Tendencywe calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. <span>Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itTo determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations.
Original toplevel document
Subject 4. Measures of Center Tendencywe calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. <span>Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itdetermine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. <span>If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. <span><body><html>
Original toplevel document
Subject 4. Measures of Center Tendencywe calculated the mean without weights, we'd get: (6 + 6.2 + 7.5) / 3 = $6.57. The fact that we've given more importance to the most recent (higher) share price inflates the weighted mean relative to the un-weighted mean. <span>Median In English, the word "mediate" means to go between or to stand in the middle of two groups, in order to act as a referee, so to speak. The median does the same thing; it is the value that stands in the middle of the data set, and divides it into two equal halves, with an equal number of data values in each half. To determine the median, arrange the data from highest to lowest (or lowest to highest) and find the middle observation. If there are an odd number of observations in the data set, the median is the middle observation (n + 1)/2 of the data set. If the number of observations is even, there is no single middle observation (there are two, actually). To find the median, take the arithmetic mean of the two middle observations. The median is less sensitive to extreme scores than the mean. This makes it a better measure than the mean for highly skewed distributions. Looking at median income is usually more informative than looking at mean income, for example. The sum of the absolute deviations of each number from the median is lower than the sum of absolute deviations from any other number. Note that whenever you calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
u calculate a median, it is imperative that you place the data in order first. It does not matter whether you order the data from smallest to largest or from largest to smallest, but it does matter that you order the data. <span>Mode Mode means fashion. The mode is the "most fashionable" number in a data set; it is the most frequently occurring score in a distribution and is used as a measure of central tendency. A set of data can have more than one mode, or even no mode. When all values are different, the data set has no mode. When a distribution has one value that appears most frequently, it is said to be unimodal. A data set that has two modes is said to be bimodal. The advantage of the mode as a measure of central tendency is that its meaning is obvious. Like the median, the mode is not affected by extreme values. Further, it is the only measure of central tendency that can be used with nominal data. The mode is greatly subject to sample fluctuations and, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
, therefore, is not recommended for use as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called "multimodal." <span>Harmonic Mean The harmonic mean of n numbers x i (where i = 1, 2, ..., n) is: The special cases of n = 2 and n = 3 are given by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed dist
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 4. Measures of Center Tendency
by: and so on. For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by: <span>The mean, median, and mode are equal in symmetric distributions. The mean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions. Extreme values affect the value of the mean, while the median is less affected by outliers. Mode helps to identify shape and skewness of distribution.<span><body><html>