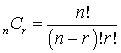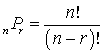Edited, memorised or added to reading queue
on 12-Aug-2017 (Sat)
Do you want BuboFlash to help you learning these things? Click here to log in or create user.
Flashcard 1436162067724
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itExamples of Explicit Costs Net income of a business reflects residual income remaining after all explicit costs have been paid. Explicit costs are the only costs necessary to calculate accounting profit. Expenses relating to advertising, supplies, utilities, inventory and equipment actually
Original toplevel document
Explicit Cost Definition | InvestopediaAn explicit cost is an expense that has occurred and has a clearly defined dollar amount. These expenses are incurred during business operations and are actual out-of-pocket cash outlays. The objective dollar amounts are subject to reporting. <span>Examples of Explicit Costs Net income of a business reflects residual income remaining after all explicit costs have been paid. Explicit costs are the only costs necessary to calculate accounting profit. Expenses relating to advertising, supplies, utilities, inventory and equipment actually purchased are examples of explicit costs. Although the depreciation of an asset is not an activity that can be tangibly traced, depreciation expense is an explicit cost because it relates to the cost of the underlying asset that the company owns. Explicit Costs vs. Implicit Costs Explicit costs arise based on what has actually been purchased as opposed to implicit costs that arise based on what has actually been given up other t
Flashcard 1438913269004
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
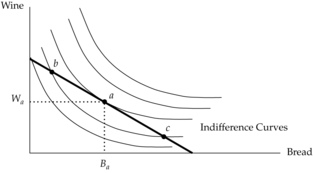
tion is the rate at which the consumer is just willing to sacrifice wine for bread. Additionally, the price ratio is the rate at which she must sacrifice wine for another slice of bread. So, at equilibrium, the consumer is just willing to pay <span>the opportunity cost that she must pay.<span><body><html>
Flashcard 1439254056204
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itLoans are made by commercial banks and repayment of these loans is guaranteed by Ex-Im Bank
Original toplevel document
Government-Assisted Foreign Buyer Financing (Eximbank USA)g may not be available in certain countries and certain terms for U.S. government policy reasons (for more information, see the Country Limitation Schedule posted on the Bank’s Web site, www.exim.gov, under the “Apply” section). <span>Key Features of Ex-Im Bank Loan Guarantees Loans are made by commercial banks and repayment of these loans is guaranteed by Ex-Im Bank. Guaranteed loans cover 100 percent of the principal and interest for 85 percent of the U.S. contract price. Interest rates are negotiable, and are usually floating and lower than fixed rates. Guaranteed loans are fully transferable, can be securitized and are available in certain foreign currencies. Guaranteed loans have a faster documentation process with the assistance of commercial banks. There are no U.S. vessel shipping requirements for amounts less than $20 million. Key Features of Ex-Im Bank Direct Loans Fixed-rate loans are provided directly to creditworthy foreign buyers. Direct loans supp
Flashcard 1442148912396
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itintangible costs and benefits are often ignored because, if they are real, they should result in cash flows at some other time.
Original toplevel document
3. BASIC PRINCIPLES OF CAPITAL BUDGETINGting relies on just a few basic principles. Capital budgeting usually uses the following assumptions: Decisions are based on cash flows. The decisions are not based on accounting concepts, such as net income. Furthermore, <span>intangible costs and benefits are often ignored because, if they are real, they should result in cash flows at some other time. Timing of cash flows is crucial. Analysts make an extraordinary effort to detail precisely when cash flows occur. Cash flows are based on opportunity cos
Flashcard 1474078051596
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itTo help improve the quality of the discussion by management, the International Accounting Standards Board (IASB) issued an exposure draft in June 2009 that proposed a framework for the preparation and presentation of management commentary.
Original toplevel document
3.1.6. Management Commentary or Management’s Discussion and Analysisthe financial statements, information included in the management commentary is typically unaudited. When using information from the management report, an analyst should be aware of whether the information is audited or unaudited. <span>To help improve the quality of the discussion by management, the International Accounting Standards Board (IASB) issued an exposure draft in June 2009 that proposed a framework for the preparation and presentation of management commentary. Per the exposure draft, that framework will provide guidance rather than set forth requirements in a standard. The exposure draft identifies five content elements of a “decision-useful
Flashcard 1611264298252
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Equity
that occurred during the accounting period in components of the stockholders' equity section of the balance sheet. For example, it includes capital transactions with owners (e.g., issuing shares) and distributions to owners (i.e., dividends). <span>The shareholders' equity section of the balance sheet lists the items in contributed capital and retained earnings on the balance sheet date. <span><body><html>
that occurred during the accounting period in components of the stockholders' equity section of the balance sheet. For example, it includes capital transactions with owners (e.g., issuing shares) and distributions to owners (i.e., dividends). <span>The shareholders' equity section of the balance sheet lists the items in contributed capital and retained earnings on the balance sheet date. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1647717780748
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Subject 10. Principles of Counting
he ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1652306873612
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Expected value
Variance is a number greater than or equal to 0 because it is the sum of squared terms. If variance is 0, there is no dispersion or risk. The outcome is certain, and the quantity X is not random at all. Variance greater than 0 indicates dispersion of outcomes. Increasing variance indicates increasing dispersion, all else
Flashcard 1652310543628
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
The shortest explanation of n factorial is that it is the number of ways to order n objects in a row. In all the problems to which we apply this counting method, we must use up all the members of a group (sampling without replacement).
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Open it
The shortest explanation of n factorial is that it is the number of ways to order n objects in a row. In all the problems to which we apply this counting method, we must use up all the members of a group (sampling without replacement).
Flashcard 1652316048652
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652318407948
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652320242956
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652322077964
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itRegarding counting, there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not.
Original toplevel document
Subject 10. Principles of Countinghe ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways can you select the stocks? Note that the order of your selection is important in this case. 10 P 2 = 10!/(10 - 2)! = 90 <span>Note that there can never be more combinations than permutations for the same problem, because permutations take into account all possible orderings of items, whereas combinations do not. <span><body><html>
Flashcard 1652323912972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itThe empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data
Original toplevel document
the+empirical+rule - Buscar con Googlertment of Statistics Online Learning! - Penn State","th":83,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcQuElAJ2v_EaT3kTk6OttMFj8vC8cwGQrbEbwExrMxvAB-IY7aQ1Nkvdoo","tw":210} <span>The empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data falls within the first standard deviation from the mean. 95% fall within two standard deviations.Nov 1, 2013 Empirical Rule: What is it? - Statistics How To www.statisticshowto.com/empirical-rule-2/ Feedback About this result People also ask What is the empirical rul
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Parent (intermediate) annotation
Open itThe empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data falls within the first standard deviation from the mean. 95% fall within two standard deviations.
Original toplevel document
the+empirical+rule - Buscar con Googlertment of Statistics Online Learning! - Penn State","th":83,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcQuElAJ2v_EaT3kTk6OttMFj8vC8cwGQrbEbwExrMxvAB-IY7aQ1Nkvdoo","tw":210} <span>The empirical rule states that for a normal distribution, nearly all of the data will fall within three standard deviations of the mean. The empirical rule can be broken down into three parts: 68% of data falls within the first standard deviation from the mean. 95% fall within two standard deviations.Nov 1, 2013 Empirical Rule: What is it? - Statistics How To www.statisticshowto.com/empirical-rule-2/ Feedback About this result People also ask What is the empirical rul
Flashcard 1652329155852
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Sequential comparisons of quarterly EPS are with the immediate prior quarter. A sequential comparison stands in contrast to a comparison with the same quarter one year ago (another frequent type o
Flashcard 1652332039436
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
the covariance between two random variables is the probability-weighted average of the cross-products of each random variable’s deviation from its own expected value.
Flashcard 1652333612300
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Multinomial Formula (General Formula for Labeling Problems). The number of ways that n objects can be labeled with kdifferent labels, with n 1 of the first type, n 2 of the second type, and so on, with n
Flashcard 1652335971596
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Multinomial Formula (General Formula for Labeling Problems). The number of ways that n objects can be labeled with kdifferent labels, with n 1 of the first type, n 2 of the second type, and so on, with n
Flashcard 1652339903756
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
Multinomial Formula (General Formula for Labeling Problems). The number of ways that n objects can be labeled with kdifferent labels, with n 1 of the first type, n 2 of the second type, and so on, with n 1 + n 2 + … + n k = n, is given by \(n!\over n1!n2!…nk!\)
Flashcard 1652342263052
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open it>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): <body><html>
Original toplevel document
Subject 10. Principles of Countingnlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
Flashcard 1652344622348
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):
Original toplevel document
Subject 10. Principles of Countingnlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
Flashcard 1652346981644
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Parent (intermediate) annotation
Open itA combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula):
Original toplevel document
Subject 10. Principles of Countingnlike the multiplication rule, factorial involves only a single group. It involves arranging items within a group, and the order of the arrangement does matter. The arrangement of ABCDE is different from the arrangement of ACBDE. <span>A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Expected value
tion mean, discussed in the reading on statistical concepts and market returns). We should distinguish expected value from the concepts of historical or sample mean. The sample mean also summarizes in a single number a central value. However, <span>the sample mean presents a central value for a particular set of observations as an equally weighted average of those observations. To summarize, the contrast is forecast versus historical, or population versus sample.<span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Expected value
pts of historical or sample mean. The sample mean also summarizes in a single number a central value. However, the sample mean presents a central value for a particular set of observations as an equally weighted average of those observations. <span>To summarize, the contrast is forecast versus historical, or population versus sample.<span><body><html>
Flashcard 1652353535244
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
To analyze a portfolio’s expected return and variance of return, we must understand these quantities are a function of characteristics of the individual securities’ returns. Looking at the dispersion or variance of portfolio return, we see that the way individual security returns move together or covary is important. To understand the significance of these movements, we need to explore some new concepts, covariance and correlation.
Flashcard 1652357205260
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
In calculations of variance we do not know whether large deviations are likely to be positive or negative, hence the degree of symmetry in return distributions.
Flashcard 1652360350988
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
l>In analyses of probabilities presented in tables, unconditional probabilities usually appear at the ends or margins of the table, hence the term marginal probability. Because of possible confusion with the way marginal is used in economics (roughly meaning incremental), we use the term unconditional probability throughout this discussion.<html>
Flashcard 1652366642444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Open it
If we know both the set of all the distinct possible outcomes of a random variable and the assignment of probabilities to those outcomes—the probability distribution of the random variable—we have a complete description of the random variable, and we can assign a probability to any event that we might describe
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Open it
If we know both the set of all the distinct possible outcomes of a random variable and the assignment of probabilities to those outcomes—the probability distribution of the random variable—we have a complete description of the random variable, and we can assign a probability to any event that we might describe
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1652374506764
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Multinominal formula
A mutual fund guide ranked 18 bond mutual funds by total returns for the year 2014. The guide also assigned each fund one of five risk labels: high risk (four funds), above-average risk (
Flashcard 1652376866060
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Multinominal formula
A mutual fund guide ranked 18 bond mutual funds by total returns for the year 2014. The guide also assigned each fund one of five risk labels: high risk (four funds), above-average risk (four funds), average risk (t
Flashcard 1652379487500
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Multinominal formula
A mutual fund guide ranked 18 bond mutual funds by total returns for the year 2014. The guide also assigned each fund one of five risk labels: high risk (four funds), above-average risk (
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Flashcard 1652389448972
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
ossible outcomes? If the answer is yes, you may be able to use a tool in this section, and you can go to the second question. If the answer is no, the number of outcomes is infinite, and the tools in this section do not apply. <span>Do I want to assign every member of a group of size n to one of n slots (or tasks)? If the answer is yes, use n factorial. If the answer is no, go to the third question. Do I want to count the number of ways to apply one of three or more labels to each member of a group? If the answer is yes
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Counting
Answering the following questions may help you apply the counting methods we have presented in this section. Does the task that I want to measure have a finite number of possible outcomes? If the answer is yes, you may be able to use a tool in this section, and you can go to the second question. If the answer is no, the number of outcomes is infinite, and the tools in this section do not apply. Do I want to assign every member of a group of size n to one of n slots (or tasks)? If the answer is yes, use n factorial. If the answer is no, go to the third question.
Flashcard 1652393381132
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
the tools in this section do not apply. Do I want to assign every member of a group of size n to one of n slots (or tasks)? If the answer is yes, use n factorial. If the answer is no, go to the third question. <span>Do I want to count the number of ways to apply one of three or more labels to each member of a group? If the answer is yes, use the multinomial formula. If the answer is no, go to the fourth question. Do I want to count the number of ways that I can choose r objects from a total of n, when the order in which I list the r
Flashcard 1652396002572
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
question. Do I want to count the number of ways to apply one of three or more labels to each member of a group? If the answer is yes, use the multinomial formula. If the answer is no, go to the fourth question. <span>Do I want to count the number of ways that I can choose r objects from a total of n, when the order in which I list the r objects does not matter (can I give the r objects a label)? If the answer to these questions is yes, the combination formula applies. If the answer is no, go to the fifth question. Do I want to count the number of ways I can choose r objects from a total of n, when the order in which I list the r objec
Flashcard 1652398361868
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Counting
al of n, when the order in which I list the r objects does not matter (can I give the r objects a label)? If the answer to these questions is yes, the combination formula applies. If the answer is no, go to the fifth question. <span>Do I want to count the number of ways I can choose r objects from a total of n, when the order in which I list the r objects is important? If the answer is yes, the permutation formula applies. If the answer is no, go to question 6. Can the multiplication rule of counting be used? If it cannot, you may have to count the possibilities one by one, or use more adv
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Counting
ant to count the number of ways I can choose r objects from a total of n, when the order in which I list the r objects is important? If the answer is yes, the permutation formula applies. If the answer is no, go to question 6. <span>Can the multiplication rule of counting be used? If it cannot, you may have to count the possibilities one by one, or use more advanced techniques than those presented here.23 <span><body><html>
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
In this reading, we have discussed the essential concepts and tools of probability. We have applied probability, expected value, and variance to a range of investment problems. A random variable is a quantity whose outcome is uncertain. Probability is a number between 0 and 1 that describes the chance that a stated event will occur. An event is a specified set of outcomes of a random var
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
sed the essential concepts and tools of probability. We have applied probability, expected value, and variance to a range of investment problems. A random variable is a quantity whose outcome is uncertain. <span>Probability is a number between 0 and 1 that describes the chance that a stated event will occur. An event is a specified set of outcomes of a random variable. Mutually exclusive events can occur only one at a time. Exhaustive events cover or contain
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
a range of investment problems. A random variable is a quantity whose outcome is uncertain. Probability is a number between 0 and 1 that describes the chance that a stated event will occur. <span>An event is a specified set of outcomes of a random variable. Mutually exclusive events can occur only one at a time. Exhaustive events cover or contain all possible outcomes. The two defining properties of a probab
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
antity whose outcome is uncertain. Probability is a number between 0 and 1 that describes the chance that a stated event will occur. An event is a specified set of outcomes of a random variable. <span>Mutually exclusive events can occur only one at a time. Exhaustive events cover or contain all possible outcomes. The two defining properties of a probability are, first, that 0 ≤ P(E) ≤ 1 (where P(E) denotes the probability of an event E), and second, that the sum of the probabilit
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
event will occur. An event is a specified set of outcomes of a random variable. Mutually exclusive events can occur only one at a time. Exhaustive events cover or contain all possible outcomes. <span>The two defining properties of a probability are, first, that 0 ≤ P(E) ≤ 1 (where P(E) denotes the probability of an event E), and second, that the sum of the probabilities of any set of mutually exclusive and exhaustive events equals 1. A probability estimated from data as a relative frequency of occurrence is an empirical probability. A probability drawing on personal or subjective judgment is a subjec
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ining properties of a probability are, first, that 0 ≤ P(E) ≤ 1 (where P(E) denotes the probability of an event E), and second, that the sum of the probabilities of any set of mutually exclusive and exhaustive events equals 1. <span>A probability estimated from data as a relative frequency of occurrence is an empirical probability. A probability drawing on personal or subjective judgment is a subjective probability. A probability obtained based on logical analysis is an a priori probability. A probability of an event E, P(E), can be stated as odds for E = P(E)/[1 − P(E)] or odds against E = [1 − P(E)]/P(E). Probabilities that are inconsistent
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
a relative frequency of occurrence is an empirical probability. A probability drawing on personal or subjective judgment is a subjective probability. A probability obtained based on logical analysis is an a priori probability. <span>A probability of an event E, P(E), can be stated as odds for E = P(E)/[1 − P(E)] or odds against E = [1 − P(E)]/P(E). Probabilities that are inconsistent create profit opportunities, according to the Dutch Book Theorem. A probability of an event not conditioned on anothe
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ve probability. A probability obtained based on logical analysis is an a priori probability. A probability of an event E, P(E), can be stated as odds for E = P(E)/[1 − P(E)] or odds against E = [1 − P(E)]/P(E). <span>Probabilities that are inconsistent create profit opportunities, according to the Dutch Book Theorem. A probability of an event not conditioned on another event is an unconditional probability. The unconditional probability of an event A is denoted P(A). Unconditional pr
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
lity of an event E, P(E), can be stated as odds for E = P(E)/[1 − P(E)] or odds against E = [1 − P(E)]/P(E). Probabilities that are inconsistent create profit opportunities, according to the Dutch Book Theorem. <span>A probability of an event not conditioned on another event is an unconditional probability. The unconditional probability of an event A is denoted P(A). Unconditional probabilities are also called marginal probabilities. A probability of an event given (conditioned on) another event is a conditional probability. The probability of an event A given an event B is denoted P(A | B).
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
13; A probability of an event not conditioned on another event is an unconditional probability. The unconditional probability of an event A is denoted P(A). Unconditional probabilities are also called marginal probabilities. <span>A probability of an event given (conditioned on) another event is a conditional probability. The probability of an event A given an event B is denoted P(A | B). The probability of both A and B occurring is the joint probability of A and B, denoted P(AB). P(A | B) = P(AB)/P(B), P(B) ≠ 0. The multip
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
abilities are also called marginal probabilities. A probability of an event given (conditioned on) another event is a conditional probability. The probability of an event A given an event B is denoted P(A | B). <span>The probability of both A and B occurring is the joint probability of A and B, denoted P(AB). P(A | B) = P(AB)/P(B), P(B) ≠ 0. The multiplication rule for probabilities is P(AB) = P(A | B)P(B). The probability that A or B occurs, o
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
on) another event is a conditional probability. The probability of an event A given an event B is denoted P(A | B). The probability of both A and B occurring is the joint probability of A and B, denoted P(AB). <span>P(A | B) = P(AB)/P(B), P(B) ≠ 0. The multiplication rule for probabilities is P(AB) = P(A | B)P(B). The probability that A or B occurs, or both occur, is denoted by P(A or B). &#
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
The probability of an event A given an event B is denoted P(A | B). The probability of both A and B occurring is the joint probability of A and B, denoted P(AB). P(A | B) = P(AB)/P(B), P(B) ≠ 0. <span>The multiplication rule for probabilities is P(AB) = P(A | B)P(B). The probability that A or B occurs, or both occur, is denoted by P(A or B). The addition rule for probabilities is P(A or B) = P(A) + P(B) − P(AB).
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
The probability of both A and B occurring is the joint probability of A and B, denoted P(AB). P(A | B) = P(AB)/P(B), P(B) ≠ 0. The multiplication rule for probabilities is P(AB) = P(A | B)P(B). <span>The probability that A or B occurs, or both occur, is denoted by P(A or B). The addition rule for probabilities is P(A or B) = P(A) + P(B) − P(AB). When events are independent, the occurrence of one event does not affect the prob
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
). P(A | B) = P(AB)/P(B), P(B) ≠ 0. The multiplication rule for probabilities is P(AB) = P(A | B)P(B). The probability that A or B occurs, or both occur, is denoted by P(A or B). <span>The addition rule for probabilities is P(A or B) = P(A) + P(B) − P(AB). When events are independent, the occurrence of one event does not affect the probability of occurrence of the other event. Otherwise, the events are dependent. &
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ule for probabilities is P(AB) = P(A | B)P(B). The probability that A or B occurs, or both occur, is denoted by P(A or B). The addition rule for probabilities is P(A or B) = P(A) + P(B) − P(AB). <span>When events are independent, the occurrence of one event does not affect the probability of occurrence of the other event. Otherwise, the events are dependent. The multiplication rule for independent events states that if A and B are independent events, P(AB) = P(A)P(B). The rule generalizes in similar fashion to more than two
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
probabilities is P(A or B) = P(A) + P(B) − P(AB). When events are independent, the occurrence of one event does not affect the probability of occurrence of the other event. Otherwise, the events are dependent. <span>The multiplication rule for independent events states that if A and B are independent events, P(AB) = P(A)P(B). The rule generalizes in similar fashion to more than two events. According to the total probability rule, if S 1 , S 2 , …, S n are mutually exclusive and exhaustive scenarios or events, then P(A) = P(A | S 1 )P(S 1 ) + P(A | S 2 )P(
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
erwise, the events are dependent. The multiplication rule for independent events states that if A and B are independent events, P(AB) = P(A)P(B). The rule generalizes in similar fashion to more than two events. <span>According to the total probability rule, if S 1 , S 2 , …, S n are mutually exclusive and exhaustive scenarios or events, then P(A) = P(A | S 1 )P(S 1 ) + P(A | S 2 )P(S 2 ) + … + P(A | S n )P(S n ). The expected value of a random variable is a probability-weighted average of the possible outcomes of the random variable. For a random variable X, the expected value of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
o events. According to the total probability rule, if S 1 , S 2 , …, S n are mutually exclusive and exhaustive scenarios or events, then P(A) = P(A | S 1 )P(S 1 ) + P(A | S 2 )P(S 2 ) + … + P(A | S n )P(S n ). <span>The expected value of a random variable is a probability-weighted average of the possible outcomes of the random variable. For a random variable X, the expected value of X is denoted E(X). The total probability rule for expected value states that E(X) = E(X | S 1 )P(S 1 ) + E(X | S 2 )P(S 2 ) + … + E(X | S n )P(S n ), where S 1 , S 2 , …, S n are mutually
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
+ P(A | S n )P(S n ). The expected value of a random variable is a probability-weighted average of the possible outcomes of the random variable. For a random variable X, the expected value of X is denoted E(X). <span>The total probability rule for expected value states that E(X) = E(X | S 1 )P(S 1 ) + E(X | S 2 )P(S 2 ) + … + E(X | S n )P(S n ), where S 1 , S 2 , …, S n are mutually exclusive and exhaustive scenarios or events. The variance of a random variable is the expected value (the probability-weighted average) of squared deviations from the random variable’s expected value E(X): σ 2 (X)
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
The total probability rule for expected value states that E(X) = E(X | S 1 )P(S 1 ) + E(X | S 2 )P(S 2 ) + … + E(X | S n )P(S n ), where S 1 , S 2 , …, S n are mutually exclusive and exhaustive scenarios or events. <span>The variance of a random variable is the expected value (the probability-weighted average) of squared deviations from the random variable’s expected value E(X): σ 2 (X) = E{[X − E(X)] 2 }, where σ 2 (X) stands for the variance of X. Variance is a measure of dispersion about the mean. Increasing variance indicates increasing dispersion. Variance is measured in squared units of the original variable.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
riance of a random variable is the expected value (the probability-weighted average) of squared deviations from the random variable’s expected value E(X): σ 2 (X) = E{[X − E(X)] 2 }, where σ 2 (X) stands for the variance of X. <span>Variance is a measure of dispersion about the mean. Increasing variance indicates increasing dispersion. Variance is measured in squared units of the original variable. Standard deviation is the positive square root of variance. Standard deviation measures dispersion (as does variance), but it is measured in the same units as the variab
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ere σ 2 (X) stands for the variance of X. Variance is a measure of dispersion about the mean. Increasing variance indicates increasing dispersion. Variance is measured in squared units of the original variable. <span>Standard deviation is the positive square root of variance. Standard deviation measures dispersion (as does variance), but it is measured in the same units as the variable. Covariance is a measure of the co-movement between random variables. The covariance between two random variables R i and R j is the expected value of t
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
uared units of the original variable. Standard deviation is the positive square root of variance. Standard deviation measures dispersion (as does variance), but it is measured in the same units as the variable. <span>Covariance is a measure of the co-movement between random variables. The covariance between two random variables R i and R j is the expected value of the cross-product of the deviations of the two random variables from their respective
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ive square root of variance. Standard deviation measures dispersion (as does variance), but it is measured in the same units as the variable. Covariance is a measure of the co-movement between random variables. <span>The covariance between two random variables R i and R j is the expected value of the cross-product of the deviations of the two random variables from their respective means: Cov(R i ,R j ) = E{[R i − E(R i )][R j − E(R j )]}. The covariance of a random variable with itself is its own variance. Correlation is a number between −1 and +1 that measures the co-movement (linear association) between two random variables: ρ(R i ,R j ) = Cov(R i ,R j )/[σ(R i ) σ(R j )
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
d value of the cross-product of the deviations of the two random variables from their respective means: Cov(R i ,R j ) = E{[R i − E(R i )][R j − E(R j )]}. The covariance of a random variable with itself is its own variance. <span>Correlation is a number between −1 and +1 that measures the co-movement (linear association) between two random variables: ρ(R i ,R j ) = Cov(R i ,R j )/[σ(R i ) σ(R j )]. To calculate the variance of return on a portfolio of n assets, the inputs needed are the n expected returns on the individual assets, n variances of return on the indiv
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
iable with itself is its own variance. Correlation is a number between −1 and +1 that measures the co-movement (linear association) between two random variables: ρ(R i ,R j ) = Cov(R i ,R j )/[σ(R i ) σ(R j )]. <span>To calculate the variance of return on a portfolio of n assets, the inputs needed are the n expected returns on the individual assets, n variances of return on the individual assets, and n(n − 1)/2 distinct covariances. Portfolio variance of return is σ2(Rp)=n∑i=1n∑j=1wiwjCov(Ri,Rj)σ2(Rp)=∑i=1n∑j=1nwiwjCov(Ri,Rj) . The calculation of covariance in a forward-looking sense
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
#13; To calculate the variance of return on a portfolio of n assets, the inputs needed are the n expected returns on the individual assets, n variances of return on the individual assets, and n(n − 1)/2 distinct covariances. <span>Portfolio variance of return is σ2(Rp)=n∑i=1n∑j=1wiwjCov(Ri,Rj)σ2(Rp)=∑i=1n∑j=1nwiwjCov(Ri,Rj) . The calculation of covariance in a forward-looking sense requires the specification of a joint probability function, which gives the probability of joint occurrences of
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ns on the individual assets, n variances of return on the individual assets, and n(n − 1)/2 distinct covariances. Portfolio variance of return is σ2(Rp)=n∑i=1n∑j=1wiwjCov(Ri,Rj)σ2(Rp)=∑i=1n∑j=1nwiwjCov(Ri,Rj) . <span>The calculation of covariance in a forward-looking sense requires the specification of a joint probability function, which gives the probability of joint occurrences of values of the two random variables. When two random variables are independent, the joint probability function is the product of the individual probability functions of the random variables.
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
Rj) . The calculation of covariance in a forward-looking sense requires the specification of a joint probability function, which gives the probability of joint occurrences of values of the two random variables. <span>When two random variables are independent, the joint probability function is the product of the individual probability functions of the random variables. Bayes’ formula is a method for updating probabilities based on new information. Bayes’ formula is expressed as follows: Updated probability of event give
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
joint occurrences of values of the two random variables. When two random variables are independent, the joint probability function is the product of the individual probability functions of the random variables. <span>Bayes’ formula is a method for updating probabilities based on new information. Bayes’ formula is expressed as follows: Updated probability of event given the new information = [(Probability of the new information given event)/(Unconditional probabi
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
es are independent, the joint probability function is the product of the individual probability functions of the random variables. Bayes’ formula is a method for updating probabilities based on new information. <span>Bayes’ formula is expressed as follows: Updated probability of event given the new information = [(Probability of the new information given event)/(Unconditional probability of the new information)] × Prior probability of event. The multiplication rule of counting says, for example, that if the first step in a process can be done in 10 ways, the second step, given the first, can be done in 5 way
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
yes’ formula is expressed as follows: Updated probability of event given the new information = [(Probability of the new information given event)/(Unconditional probability of the new information)] × Prior probability of event. <span>The multiplication rule of counting says, for example, that if the first step in a process can be done in 10 ways, the second step, given the first, can be done in 5 ways, and the third step, given the first two, can be done in 7 ways, then the steps can be carried out in (10)(5)(7) = 350 ways. The number of ways to assign every member of a group of size n to n slots is n! = n (n − 1) (n − 2)(n − 3) … 1. (By convention, 0! = 1.) The number of wa
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
rst step in a process can be done in 10 ways, the second step, given the first, can be done in 5 ways, and the third step, given the first two, can be done in 7 ways, then the steps can be carried out in (10)(5)(7) = 350 ways. <span>The number of ways to assign every member of a group of size n to n slots is n! = n (n − 1) (n − 2)(n − 3) … 1. (By convention, 0! = 1.) The number of ways that n objects can be labeled with k different labels, with n 1 of the first type, n 2 of the second type, and so on, with n 1 + n 2 + … + n k =
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
ne in 7 ways, then the steps can be carried out in (10)(5)(7) = 350 ways. The number of ways to assign every member of a group of size n to n slots is n! = n (n − 1) (n − 2)(n − 3) … 1. (By convention, 0! = 1.) <span>The number of ways that n objects can be labeled with k different labels, with n 1 of the first type, n 2 of the second type, and so on, with n 1 + n 2 + … + n k = n, is given by n!/(n 1 !n 2 ! … n k !). This expression is the multinomial formula. A special case of the multinomial formula is the combination formula. The number of ways to choose r objects from a total of n objects, when the order in which the robje
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
objects can be labeled with k different labels, with n 1 of the first type, n 2 of the second type, and so on, with n 1 + n 2 + … + n k = n, is given by n!/(n 1 !n 2 ! … n k !). This expression is the multinomial formula. <span>A special case of the multinomial formula is the combination formula. The number of ways to choose r objects from a total of n objects, when the order in which the robjects are listed does not matter, is nCr=(nr)=n!(n−r)!r!nCr=(nr)=n!(n−r)!r! The number of ways to choose r objects from a total of n objects, when the order in which the r objects are listed does matter, is nPr=n!(n
| status | not read | reprioritisations | ||
|---|---|---|---|---|
| last reprioritisation on | suggested re-reading day | |||
| started reading on | finished reading on |
Summary
he combination formula. The number of ways to choose r objects from a total of n objects, when the order in which the robjects are listed does not matter, is nCr=(nr)=n!(n−r)!r!nCr=(nr)=n!(n−r)!r! <span>The number of ways to choose r objects from a total of n objects, when the order in which the r objects are listed does matter, is nPr=n!(n−r)!nPr=n!(n−r)! This expression is the permutation formula. <span><body><html>
Flashcard 1652462587148
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 10. Principles of Counting
(The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. <span>An ordered listing is known as a permutation, and the formula that counts the number of permutations is known as the permutation formula. The number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does matter, is: For example, if you select two of the ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways ca
(The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. <span>An ordered listing is known as a permutation, and the formula that counts the number of permutations is known as the permutation formula. The number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does matter, is: For example, if you select two of the ten stocks you are analyzing and invest $10,000 in one stock and $20,000 in another stock, how many ways ca
Flashcard 1652464946444
| status | not learned | measured difficulty | 37% [default] | last interval [days] | |||
|---|---|---|---|---|---|---|---|
| repetition number in this series | 0 | memorised on | scheduled repetition | ||||
| scheduled repetition interval | last repetition or drill |
Subject 10. Principles of Counting
A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (<span>The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &
A combination is a listing in which the order of listing does not matter. This describes the number of ways that we can choose r objects from a total of n objects, where the order in which the r objects is listed does not matter (<span>The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. &