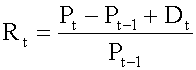BuboFlash - helps with learning

Edited, memorised or added to reading queue

Do you want BuboFlash to help you learning these things? Click here to log in or create user.

Flashcard 1464617798924

Tags

#conversation-tactics

Question

Chapter 9. How to deflect [...]

Answer

and roll with the punches.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Open it
Chapter 9. How to deflect and roll with the punches.

Original toplevel document (pdf)

cannot see any pdfs

Flashcard 1480013778188

Tags

#power-of-habit

Question

What happened to the rats brain the first time it needed to find the cheese?

Answer

All kinds of places in the brain fired up specially the basal ganglia

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1603697511692

Tags

#excel-stuff

Question

Cual es la formula para un hipervinculo a una hoja en el mismo libro?

Answer

# 'El nombre de la hoja' !A1

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1621034405132

Tags

#cashflow-statement

Question

FCF accounts for [...] and dividend payments, which are essential to the ongoing nature of the business.

Answer

capital expenditures

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Cash Flow Statement Analysis
CFO. CFO does not include cash outlays for replacing old equipment. Free Cash Flow (FCF) is intended to measure the cash available to a company for discretionary uses after making all required cash outlays. It accounts for capital expenditures and dividend payments, which are essential to the ongoing nature of the business. The basic definition is cash from operations less the amount of capital expenditures required to maintain the company's present productive capacity. &#

Flashcard 1621041483020

Tags

#cashflow-statement

Question

[...]: Cash available to shareholders and bondholders after taxes, capital investment, and WC investment.

Answer

Free Cash Flow to the Firm (FCFF)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Cash Flow Statement Analysis
3; The basic definition is cash from operations less the amount of capital expenditures required to maintain the company's present productive capacity. Free cash flow = CFO - capital expenditure Free Cash Flow to the Firm (FCFF): Cash available to shareholders and bondholders after taxes, capital investment, and WC investment. FCFF = NI + NCC + Int (1 - Tax rate) - FCInv - WCInv NI: Net income available to common shareholders. It is the com

Flashcard 1621274529036

Tags

#cashflow-statement

Question

The add-back of net non-cash expenses is usually positive or negative?

Answer

Positive

because depreciation is a major part of total expenses for most companies.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Cash Flow Statement Analysis
; Free cash flow = CFO - capital expenditure Free Cash Flow to the Firm (FCFF): Cash available to shareholders and bondholders after taxes, capital investment, and WC investment. FCFF = NI + NCC + Int (1 - Tax rate) - FCInv - WCInv NI: Net income available to common shareholders. It is the company's earnings after interest, taxes and preferred dividends. NCC: Net non-cash

Flashcard 1621276364044

Tags

#cashflow-statement

Question

The add-back of net non-cash expenses is usually positive because [...]

Answer

depreciation is a major part of total expenses for most companies.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1621291830540

Tags

#reading-6-time-value-of-money

Question

Why is money worth more today than in the future?

Answer

This is because the $1 today can be invested to earn interest immediately.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
The time value of money (TVM) refers to the fact that $1 today is worth more than $1 in the future. This is because the $1 today can be invested to earn interest immediately. The TVM reflects the relationship between present value, future value, time, and interest rate. The time value of money underlies rates of return, interest rates, required rates of retu

Flashcard 1621294189836

Tags

#reading-6-time-value-of-money

Question

The TVM reflects the relationship between [...] , future value, time, and [...] .

Answer

present value

interest rate

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1621296549132

Tags

#reading-6-time-value-of-money

Question

There are [...] ways to interpret interest rates

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
interest rate. The time value of money underlies rates of return, interest rates, required rates of return, discount rates, opportunity costs, inflation, and risk. It reflects the relationship between time, cash flow, and interest rate. There are three ways to interpret interest rates: Required rate of return is the return required by investors or lenders to postpone their current consumption. Discount rate is the rate used to discount future cash flows

Flashcard 1621298908428

Tags

#reading-6-time-value-of-money

Question

[...] is the return required by investors or lenders to postpone their current consumption.

Answer

Required rate of return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
n, interest rates, required rates of return, discount rates, opportunity costs, inflation, and risk. It reflects the relationship between time, cash flow, and interest rate. There are three ways to interpret interest rates: Required rate of return is the return required by investors or lenders to postpone their current consumption. Discount rate is the rate used to discount future cash flows to allow for the time value of money (that is, to bring a future value equivalent to present value). Opportunity cost is the

Flashcard 1621303627020

Tags

#reading-6-time-value-of-money

Question

[...] is the most valuable alternative investors give up when they choose what to do with money.

Answer

Opportunity cost

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
e return required by investors or lenders to postpone their current consumption. Discount rate is the rate used to discount future cash flows to allow for the time value of money (that is, to bring a future value equivalent to present value). Opportunity cost is the most valuable alternative investors give up when they choose what to do with money. In a certain world, the interest rate is called the risk-free rate. For investors preferring current to future consumption, the risk-free interest rate is the rate of compensation

Flashcard 1621308345612

Tags

#reading-6-time-value-of-money

Question

The [...] consists of the real rate (a pure rate of interest) and an inflation premium.

Answer

nominal cost of money

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
licate interest rates: Inflation: When prices are expected to increase, lenders charge not only an opportunity cost for postponing consumption but also an inflation premium that takes into account the expected increase in prices. The nominal cost of money consists of the real rate (a pure rate of interest) and an inflation premium. Risk: Companies exhibit varying degrees of uncertainty concerning their ability to repay lenders. Lenders therefore charge interest rates that incorporate default

Flashcard 1621317782796

Tags

#reading-6-time-value-of-money

Question

[...] occurs when the number of compounding periods becomes infinite.

Answer

Continuous compounding

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
nominal risk-free rate (real rate + an inflation premium) and a default risk premium. Compounding is the process of accumulating interest over a period of time. A compounding period is the number of times per year that interest is paid. Continuous compounding occurs when the number of compounding periods becomes infinite; interest is added continuously. Discounting is the calculation of the present value of some known future value. Discount rate is the rate used to calculate the present value of some future cash flow. Disco

Flashcard 1621322501388

Tags

#reading-6-time-value-of-money

Question

[...] is the rate used to calculate the present value of some future cash flow.

Answer

Discount rate

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
per year that interest is paid. Continuous compounding occurs when the number of compounding periods becomes infinite; interest is added continuously. Discounting is the calculation of the present value of some known future value. Discount rate is the rate used to calculate the present value of some future cash flow. Discounted cash flow is the present value of some future cash flow. <body><html>

Flashcard 1621324860684

Tags

#reading-6-time-value-of-money

Question

[...] is the present value of some future cash flow.

Answer

Discounted cash flow

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1 Time Value of Money and Interest Rates
ding periods becomes infinite; interest is added continuously. Discounting is the calculation of the present value of some known future value. Discount rate is the rate used to calculate the present value of some future cash flow. Discounted cash flow is the present value of some future cash flow. <body><html>

Flashcard 1621957676300

Tags

#reading-6-time-value-of-money

Question

Formula

EAR = [...]

Answer

(1 + periodic interest rate)^m - 1

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622917909772

Tags

#discounted-cashflow-applications

Question

is the allocation of funds to relatively long-range projects or investments.

Answer

Capital budgeting

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622919744780

Tags

#discounted-cashflow-applications

Question

Management of a company’s short-term assets.

Answer

Working capital management

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622922366220

Tags

#discounted-cashflow-applications

Question

The [...] of an investment is the present value of its cash inflows minus the present value of its cash outflows.

Answer

net present value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622938619148

Tags

#discounted-cashflow-applications

Question

The discount rate that makes the present value of an investment’s costs equal to the present value of the investment’s benefits.

Answer

IRR

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622941502732

Tags

#discounted-cashflow-applications

Question

What is the IRR rule?

Answer

Projects or investments for which the IRR is greater than the opportunity cost of capital should be accepted

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1622943337740

Tags

#discounted-cashflow-applications

Question

The IRR rule uses [...] as a hurdle rate

Answer

the opportunity cost of capital

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623556754700

Tags

#discounted-cashflow-applications

Question

When the IRR and NPV rules conflict in ranking projects, we should take directions from [...]

Answer

the NPV rule.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623560424716

Tags

#discounted-cashflow-applications

Question

Why should we choose the NPV rule over the IRR rule when analyzing mutually exclusive projects?

Answer

The NPV of an investment represents the expected addition to shareholder wealth from an investment.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623792160012

Tags

#discounted-cashflow-applications

Question

The Money-Weighted rate of return is an [...] calculation.

Answer

internal rate of return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623807888652

Tags

#discounted-cashflow-applications

Question

In the United States, the money-weighted return is frequently called the [...]

Answer

dollar-weighted return.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623815228684

Tags

#discounted-cashflow-applications

Question

If you are an investor and you want to assess the success of your investments, which two tasks do you face?

Answer

performance measurement

performance appraisal.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623818636556

Tags

#discounted-cashflow-applications

Question

The calculation of returns in a logical and consistent manner is called [...]

Answer

performance measurement

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623824403724

Tags

#discounted-cashflow-applications

Question

Accurate performance measurement provides the basis for your second task, [...] .

Answer

performance appraisal

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623830695180

Tags

#discounted-cashflow-applications

Question

The return that an investor earns during a specified holding period; a synonym for total return.

Answer

Holding period return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623834103052

Tags

#discounted-cashflow-applications

Question

HPR = [...]

Answer

(P₁ − P₀ + D₁)/P₀

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1623849307404

Tags

#discounted-cashflow-applications

Question

Two of the measurement tools available for portfolio perfomance measure are the [...] measure and the [...] measure.

Answer

money-weighted rate of return

time-weighted rate of return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624281058572

Tags

#discounted-cashflow-applications

Question

An investment measure that is not sensitive to the additions and withdrawals of funds is the [...]

Answer

time-weighted rate of return.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624283155724

Tags

#discounted-cashflow-applications

Question

What is the preferred performance measure in the investment management industry?

Answer

time-weighted rate of return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624287350028

Tags

#discounted-cashflow-applications

Question

The [...] rate of return is not affected by cash withdrawals or additions to the portfolio.

Answer

time-weighted rate of return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624656448780

Tags

#discounted-cashflow-applications

Question

The [...] is the market for short-term debt instruments (one-year maturity or less).

Answer

money market

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624658283788

Tags

#discounted-cashflow-applications

Question

[...] pay interest as the difference between the amount borrowed and the amount paid back.

Answer

pure discount instruments

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1624660380940

Tags

#discounted-cashflow-applications

Question

The [...] of a T-bill is the amount the US government promises to pay back to a T-bill investor.

Answer

face value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1626637208844

Tags

#reading-7-discounted-cashflows-applications

Question

The IRR assumes that all project cash flows can be reinvested to earn [...]

Answer

a rate of return exactly equal to the IRR itself.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1. NPV and IRR
le. Reinvestment The IRR is intended to provide a single number that represents the rate of return generated by a capital investment. As such, it is an easy number to interpret and understand. However, calculation of the IRR assumes that all project cash flows can be reinvested to earn a rate of return exactly equal to the IRR itself. In other words, a project with an IRR of 6% assumes that all cash flows can be reinvested to earn exactly 6%. If the cash flows are invested at a rate lower than 6%, the realized return

Flashcard 1626644286732

Tags

#reading-7-discounted-cashflows-applications

Question

Why is Timing of cashflows an issue with IRR?

Answer

Since IRR supposes the reinvestment of the funds at the same rate the distance between cashflows can make a substantial difference

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 1. NPV and IRR
usive projects of greatly differing scale: one that requires a relatively small investment and returns relatively small cash flows, and another that requires a much larger investment and returns much larger cash flows. Timing The other situation in which IRR is likely to contradict NPV is when there are two mutually-exclusive projects whose cash flows are timed very differently: one that receives its

Flashcard 1626650053900

Tags

#reading-7-discounted-cashflows-applications

Question

When analyzing rates of return, our starting point is the [...]

Answer

holding period return (HPR).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1626652413196

Tags

#reading-7-discounted-cashflows-applications

Question

Holding period return (HPR) is also called...

Answer

total return, or

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1626654772492

Tags

#reading-7-discounted-cashflows-applications

Question

[...] measures the total return for holding an investment over a certain period of time

Answer

HPR

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 2. Holding Period Return
When analyzing rates of return, our starting point is the total return, or holding period return (HPR). HPR measures the total return for holding an investment over a certain period of time, and can be calculated using the following formula: P t = price per share at the end of time period t P (t-1) = price per share at the

Flashcard 1626657131788

Tags

#has-images #reading-7-discounted-cashflows-applications

Question

Holding period return formula

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1631884021004

Tags

#reading-7-discounted-cashflows-applications

Question

The dollar-weighted rate of return is essentially the [...] on a portfolio.

Answer

internal rate of return (IRR)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Dollar-weighted and Time-weighted Rates of Return
The dollar-weighted rate of return is essentially the internal rate of return (IRR) on a portfolio. This approach considers the timing and amountof cash flows. It is affected by the timing of cash flows. If funds are added to a portfolio when the portfolio is performing well (poorly),

Flashcard 1631928585484

Tags

#reading-7-discounted-cashflows-applications

Question

The time-weighted rate of return measures the [...] of $1 initial investment over the measurement period.

Answer

compound growth rate

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Dollar-weighted and Time-weighted Rates of Return
rs the timing and amountof cash flows. It is affected by the timing of cash flows. If funds are added to a portfolio when the portfolio is performing well (poorly), the dollar-weighted rate of return will be inflated (depressed). The time-weighted rate of return measures the compound growth rate of $1 initial investment over the measurement period. Time-weightedmeans that returns are averaged over time. This approach is not affected by the timing of cash flows; therefore, it is the preferred method of performance measurement. &#13

Flashcard 1632046812428

Tags

#reading-7-discounted-cashflows-applications

Question

When Calculating the time-weighted rate of return:

If the measurement period > 1 year, [...]

Answer

take the geometric mean of the annual returns.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Dollar-weighted and Time-weighted Rates of Return
For the second year, HPR 2 : (280 + 20)/300 - 1 = 0. Calculate the time-weighted rate of return: If the measurement period < 1 year, compound holding period returns to get an annualized rate of return for the year. If the measurement period > 1 year, take the geometric mean of the annual returns. <body><html>

Flashcard 1632835865868

Tags

#reading-7-discounted-cashflows-applications

Question

Bank discount yield is not a meaningful measure of the return on investment because:

It is based on [...] , not on the [...] .
It is annualized using a 360-day year, not a 365-day year.
It annualizes with simple interest and ignores the effect of interest on interest (compound interest).

Answer

the face value

purchase price

Instead, return on investment should be measured based on cost of investment.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
unt basis D = the dollar discount, which is equal to the difference between the face value of the bill, F, and its purchase price, P t = the number of days remaining to maturity 360 = the bank convention of the number of days in a year. Bank discount yield is not a meaningful measure of the return on investment because: It is based on the face value, not on the purchase price. Instead, return on investment should be measured based on cost of investment. It is annualized using a 360-day year, not a 365-day year. It annualizes with simple interest and ignores the effect of interest on interest (compound interest). Holding period yield (HPY) is the return earned by an investor if the money market instrument is held until maturity: P 0 =

Flashcard 1632864439564

Tags

#reading-7-discounted-cashflows-applications

Question

Bank discount yield is not a meaningful measure of the return on investment because:

It is based on the face value , not on the purchase price.
It is [...] .
It annualizes with simple interest and ignores the effect of interest on interest (compound interest).

Answer

annualized using a 360-day year, not a 365-day year

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1632883051788

Tags

#reading-7-discounted-cashflows-applications

Question

Bank discount yield is not a meaningful measure of the return on investment because:

It is based on the face value , not on the purchase price.
It is annualized using a 360-day year, not a 365-day year.
It [...]

Answer

annualizes with simple interest

ignores the effect of interest on interest (compound interest).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1633376668940

Tags

#reading-7-discounted-cashflows-applications

Question

If we know HPY, then:

r_MM = [...]

Answer

HPY x 360/t

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
990. Bank discount yield: (1000 - 990)/1000 x 360/60 = 6% Holding period yield: (1000 - 990)/990 = 1.0101% Effective annual yield: (1 + 1.0101%) 365/60 - 1 = 6.3047% Money market yield: (360 x 6%)/(360 - 60 x 6%) = 6.0606% If we know HPY, then: EAY = (1 + HPY) 365/t - 1 r MM = HPY x 360/t If we know EAY, then: HPY = ( 1 + EAY) t/365 - 1 r MM = [(1 + EAY) t/365 - 1] x (360/t) If we know r MM , then: HPY = r MM x (t/360) EAY = (1 + r

Flashcard 1633419398412

Tags

#reading-7-discounted-cashflows-applications

Question

If we know r_MM, then:

EAY = ( [...] )^365/t - 1

Answer

1 + r_MM x t/360

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
ld: (360 x 6%)/(360 - 60 x 6%) = 6.0606% If we know HPY, then: EAY = (1 + HPY) 365/t - 1 r MM = HPY x 360/t If we know EAY, then: HPY = ( 1 + EAY) t/365 - 1 r MM = [(1 + EAY) t/365 - 1] x (360/t) If we know r MM , then: HPY = r MM x (t/360) EAY = (1 + r MM x t/360) 365/t - 1 <body><html>

Flashcard 1634082884876

Tags

#reading-7-discounted-cashflows-applications

Question

U.S. bonds typically make [...] payments per year.

Answer

two coupon

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 5. Bond Equivalent Yield
Periodic bond yields for both straight and zero-coupon bonds are conventionally computed based on semi-annual periods, as U.S. bonds typically make two coupon payments per year. For example, a zero-coupon bond with a maturity of five years will mature in 10 6-month periods. The periodic yield for that bond, r, is indicated by the equation Price = Maturity value

Flashcard 1634085244172

Tags

#reading-7-discounted-cashflows-applications

Question

What is the quickest way to convert BEY to YTM?

Answer

Convertir interes nominal a efectivo en la calculadora

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 5. Bond Equivalent Yield
y. This method ignores the effect of compounding semi-annual YTM, and the YTM calculated in this way is called a bond-equivalent yield (BEY). However, yields of a semi-annual-pay and an annual-pay bond cannot be compared directly without conversion. This conversion can be done in one of the two ways: Convert the bond-equivalent yield of a semi-annual-pay bond to an annual-pay bond.

Flashcard 1634645445900

Tags

#reading-7-discounted-cashflows-applications

Question

The effective annual yield is the annualized HPY on the basis of a [...]

Answer

365-day year.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
#13; Since a pure discount instrument (e.g., a T-bill) makes no interest payment, its HPY is (P 1 - P 0 )/P 0 . Note that HPY is computed on the basis of purchase price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of

Flashcard 1635073789196

Tags

#discounted-cashflow-applications

Question

The money-weighted rate of return has a serious drawback that involves clients, what is it?

Answer

Clients determine when money is given to the investment manager and those decisions may significantly influence the money-weighted rate of return.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

Original toplevel document

Open it
The money-weighted rate of return has a serious drawback. Generally, clients determine when money is given to the investment manager and those decisions may significantly influence the money-weighted rate of return . A general principle of evaluation, however, is that a person or entity should be judged only on the basis of their own actions, or actions under their control. An evaluation tool should

Flashcard 1635080604940

Tags

#statistical-concepts-and-market-returns

Question

central tendency analyzes [...]

Answer

where the returns are centered

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Open it
where the returns are centered (central tendency); how far returns are dispersed from their center (dispersion); whether the distribution of returns is symmetrically shaped or lopsided (skewness); and &#1

Flashcard 1635085585676

Tags

#statistical-concepts-and-market-returns

Question

skewness analyzes whether the distribution of returns is [...]

Answer

symmetrically shaped or lopsided

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635088469260

Tags

#statistical-concepts-and-market-returns

Question

The term statistics can have two broad meanings, one referring to [...] and the other to [...]

Answer

data

method.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635091352844

Tags

#statistical-concepts-and-market-returns

Question

A quantity computed from or used to describe a sample of data is called a [...]

Answer

Statistic

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635094236428

Tags

#statistical-concepts-and-market-returns

Question

[...] is the study of how data can be summarized effectively to describe the important aspects of large data sets.

Answer

Descriptive statistics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635096071436

Tags

#statistical-concepts-and-market-returns

Question

[...] involves making forecasts, estimates, or judgments about a larger group from the smaller group actually observed.

Answer

Statistical inference

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635097906444

Tags

#statistical-concepts-and-market-returns

Question

The foundation for statistical inference is [...]

Answer

probability theory

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635101576460

Tags

#statistical-concepts-and-market-returns

Question

A sample is a [...]

Answer

subset of a population.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635103411468

Tags

#statistical-concepts-and-market-returns

Question

Any descriptive measure of a population characteristic is called a [...]

Answer

parameter.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635110751500

Tags

#statistical-concepts-and-market-returns

Question

The four types of measurement scales are [...]

Answer

nominal, ordinal, interval, and ratio.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635112586508

Tags

#statistical-concepts-and-market-returns

Question

The acronym for measurement of scale is [...]

Answer

NOIR

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635118091532

Tags

#statistical-concepts-and-market-returns

Question

A [...] is a tabular display of data summarized into a relatively small number of intervals.

Answer

frequency distribution

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635119926540

Tags

#statistical-concepts-and-market-returns

Question

When we analyze rates of return, our starting point is [...]

Answer

the holding period return

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635128315148

Tags

#statistical-concepts-and-market-returns

Question

An [...] is a set of values within which an observation falls.

(Frequency distribution)

Answer

interval

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635134344460

Tags

#statistical-concepts-and-market-returns

Question

We represent an interval with the letter [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635138014476

Tags

#statistical-concepts-and-market-returns

Question

The [...] cumulates (adds up) the relative frequencies as we move from the first to the last interval.

Answer

cumulative relative frequency

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635139849484

Tags

#statistical-concepts-and-market-returns

Question

A [...] is a bar chart of data that have been grouped into a frequency distribution.

Answer

histogram

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635149286668

Tags

#statistical-concepts-and-market-returns

Question

The [...] is the sum of the observations divided by the number of observations.

Answer

arithmetic mean

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635152956684

Tags

#statistical-concepts-and-market-returns

Question

The population mean is represented by the greek letter [...],

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635156626700

Tags

#statistical-concepts-and-market-returns

Question

The sample mean or average is represented with the letter

Answer

$\bar {X} $ (read “X-bar”

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1635158461708

Tags

#statistical-concepts-and-market-returns

Question

Observations over individual units at a point in time, as opposed to time-series data.

Answer

Cross sectional data

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636296166668

Tags

#reading-7-discounted-cashflows-applications

Question

Is Bank discount yield a meaningful measure of the return on investment?

Answer

not

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636857941260

Tags

#reading-9-probability-concepts

Question

[...] is a procedure for updating beliefs based on new information.

Answer

Bayes’ formula

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636859776268

Tags

#reading-9-probability-concepts

Question

In probability, the return on a risky asset is an example of a [...]

Answer

random variable

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636866067724

Tags

#reading-9-probability-concepts

Question

An [...] is a specified set of outcomes.

Answer

event

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636869999884

Tags

#reading-9-probability-concepts

Question

A [...] is a number between 0 and 1 describing the chance that a stated event will occur.

Answer

Probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636879174924

Tags

#reading-9-probability-concepts

Question

If A, B, and C are mutually exclusive and exhaustive events then P(A) + P(B) + P(C) = [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1636948905228

Tags

#reading-9-probability-concepts

Question

The probability of any event is the [...] included in the definition of the event.

Answer

sum of the probabilities of the distinct outcomes

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637148134668

Tags

#reading-9-probability-concepts

Question

Can we ecalculate an empirical probability of an event not in the historical record?

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637161766156

Tags

#reading-9-probability-concepts

Question

Because a priori and empirical probabilities generally do not vary from person to person, they are often grouped as [...]

Answer

objective probabilities.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637196893452

Tags

#reading-9-probability-concepts

Question

A result in probability theory stating that inconsistent probabilities create profit opportunities.

Answer

Dutch book theorem

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637206592780

Tags

#reading-9-probability-concepts

Question

An unconditional probability is also called [...]

Answer

a Marginal Probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637210524940

Tags

#reading-9-probability-concepts

Question

A fraction is made up of two integers—one on the top, and one on the bottom. The top one is called the [...] , the bottom one is called the [...]

Answer

numerator

denominator

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637214457100

Tags

#reading-9-probability-concepts

Question

In the question “What is the probability of A, given that B has occurred?” The probability in answer to this last question is a [...]

Answer

conditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637258759436

Tags

#reading-9-probability-concepts

Question

[...] (read: “the probability of A given B”).

Answer

P(A | B)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637266099468

Tags

#reading-9-probability-concepts

Question

[...] (read: “the probability of A and B”).

Answer

P(AB)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637269769484

Tags

#reading-9-probability-concepts

Question

The conditional probability of A given that B has occurred is equal to the [...] divided by [...] (assumed not to equal 0).

Answer

joint probability of A and B divided by the probability of B

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1637564157196

Tags

#reading-9-probability-concepts

Question

Wagering meaning

Answer

Apostar

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Odds
y’s EPS for FY2014 beating $0.69 are 1 to 7 means that the speaker believes the probability of the event is 1/(1 + 7) = 1/8 = 0.125. Odds against E = [1 − P(E)]/P(E), the reciprocal of odds for E. Given odds against E of “a to b,” the implied probability of E is b/(a + b). The statement that the odds against the company’s EPS for FY2014 beating $0.69 are 15 to 1 is consistent with a belief that the probability of the event is

Flashcard 1637588798732

Tags

#reading-7-discounted-cashflows-applications

Question

Is the Money market yield annualized as compounded interest or simple interest?

Answer

Simple

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Different Yield Measures of a U.S. Treasury Bill
se price, not face value. It is not an annualized yield. The effective annual yield is the annualized HPY on the basis of a 365-day year. It incorporates the effect of compounding interest. Money market yield (also known as CD equivalent yield) is the annualized HPY on the basis of a 360-day year using simple interest. Example An investor buys a $1,000 face-value T-bill due in 60 days at a price of $990. Bank discount yield: (1000 - 990

Flashcard 1637678451980

Tags

#reading-9-probability-concepts

Question

The odds of success are the ratio of [...]

Answer

success to failure S:F

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1640988544268

Tags

#discounted-cashflow-applications

Question

Can I calculate the dollar weighted return if t=0 is unknown?

Answer

No, you need to know every cashflow

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1641040448780

Tags

#statistical-concepts-and-market-returns

Question

The letter k represents [...]

Answer

an interval

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644831837452

Tags

#reading-9-probability-concepts

Question

A quantity whose future outcomes are uncertain.

Answer

Random variable

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644833672460

Tags

#reading-9-probability-concepts

Question

A possible value of a random variable.

Answer

Outcome

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644835769612

Tags

#reading-9-probability-concepts

Question

Any outcome or specified set of outcomes of a random variable.

Answer

Event

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644840488204

Tags

#reading-9-probability-concepts

Question

We use [...] to highlight statements that define events.

Answer

italics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644842585356

Tags

#reading-9-probability-concepts

Question

A number between 0 and 1 describing the chance that a stated event will occur.

Answer

Probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644844682508

Tags

#reading-9-probability-concepts

Question

Covering or containing all possible outcomes.

Answer

Exhaustive

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644847041804

Tags

#reading-9-probability-concepts

Question

The probability of an event estimated as a relative frequency of occurrence.

Answer

Empirical probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644849401100

Tags

#reading-9-probability-concepts

Question

A probability drawing on personal or subjective judgment.

Answer

Subjective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644851236108

Tags

#reading-9-probability-concepts

Question

A probability based on logical analysis rather than on observation or personal judgment.

Answer

A priori probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644853071116

Tags

#reading-9-probability-concepts

Question

Probabilities that generally do not vary from person to person; includes a priori and empirical probabilities.

Answer

Objective probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644864605452

Tags

#reading-9-probability-concepts

Question

A result in probability theory stating that inconsistent probabilities create profit opportunities.

Answer

Dutch book theorem

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644869061900

Tags

#reading-9-probability-concepts

Question

The probability of an event not conditioned on another event.

Answer

Unconditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644872731916

Tags

#reading-9-probability-concepts

Question

The probability of an event given (conditioned on) another event.

Answer

Conditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644876664076

Tags

#reading-9-probability-concepts

Question

The probability of the joint occurrence of stated events.

Answer

Joint probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644878761228

Tags

#reading-9-probability-concepts

Question

The rule that the joint probability of events A and B equals the probability of A given B times the probability of B.

Answer

Multiplication rule for probabilities

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644886363404

Tags

#reading-9-probability-concepts

Question

it is common to use a [...] to represent a defined event.

Answer

capital letter in italics

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644888198412

Tags

#reading-9-probability-concepts

Question

The sum of the probabilities of any set of mutually exclusive and exhaustive events equals [...] .

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644892130572

Tags

#reading-9-probability-concepts

Question

The probability of any event is the sum of the probabilities of [...]

Answer

the distinct outcomes included in the definition of the event.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644904975628

Tags

#reading-9-probability-concepts

Question

Given odds for E of “a to b,” the implied probability of E is [...]

Answer

a/(a + b).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644908907788

Tags

#reading-9-probability-concepts

Question

Odds against are the [...] of odds for E

Answer

reciprocal

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644920442124

Tags

#reading-9-probability-concepts

Question

“What is the probability of this event A?” is an [...]

Answer

unconditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644922277132

Tags

#reading-9-probability-concepts

Question

Unconditional probability is also frequently referred to as [...]

Answer

marginal probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644924898572

Tags

#reading-9-probability-concepts

Question

The denominator in an unconditional probability is [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644926733580

Tags

#reading-9-probability-concepts

Question

The denominator in an conditional probability is [...] of the event that conditions it.

Answer

the sum of the probabilities for all outcomes

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644928830732

Tags

#reading-9-probability-concepts

Question

“What is the probability of A, given that B has occurred?” The probability in answer to this last question is a [...]

Answer

conditional probability

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644932500748

Tags

#reading-9-probability-concepts

Question

To state an exact definition of conditional probability, we first need to introduce the concept of [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644934860044

Tags

#reading-9-probability-concepts

Question

“What is the probability of both A and B happening?” The answer to this question is a [...]

Answer

joint probability.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644936695052

Tags

#reading-9-probability-concepts

Question

[...] (read: “the probability of A and B”)

Answer

P(AB)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1644938530060

Tags

#reading-9-probability-concepts

Question

The joint probability of A and B is the [...]

Answer

sum of the probabilities of the outcomes they have in common.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1645005114636

Tags

#analysts-questions

Question

To find quantiles in a frequency distribution you have to know [...]

Answer

cumulative frequency

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1645231082764

Tags

#reading-9-probability-concepts

Question

the [...] of an experiment or random trial is the set of all possible outcomes or results of that experiment.

Answer

sample space

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

https://www.google.com.mx/search?q=sample%2Bspace%2Bprobability&rlz=1C5CHFA_enMX588MX588&oq=sample%2Bspace%2Bproba&aqs=chrome.0.0j69i57j0l4.4172j0j1&sourceid=chrome&ie=UTF-8
t":"Math Goodies","th":98,"tu":"https://encrypted-tbn0.gstatic.com/images?q\u003dtbn:ANd9GcQcW8yGVex34TZK0u33zmGPrJUYi4Sw9vz1DI4e1YYbbQn3bEVPNVAGcXN2","tw":216} In probability theory, the sample space of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes are listed as elements in the set. Sample space - Wikipedia https://en.wikipedia.org/wiki/Sam

Flashcard 1645290851596

Tags

#reading-9-probability-concepts

Question

The complement of event A is [...]

Answer

the event that A does not occur.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 2. Unconditional, Conditional, and Joint Probabilities
The complement of event A is the event that A does not occur. It is expressed as A c . The probabilities of an event and its complement must have a sum of 1: P(A) + P(A c ) = 1. Note that event A and its complement, A c , are mutually exclusive (t

Flashcard 1645293210892

Tags

#reading-9-probability-concepts

Question

The [...] is expressed as A^c

Answer

complement of event A

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1645890637068

Tags

#reading-9-probability-concepts

Question

If events A and B are mutually exclusive, the joint probability of A and B is [...]

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 3. Addition Rule for Probabilities: the Probability that at Least One of Two Events Will Occur
P(A or B) = P(A) + P(B) - P(AB) The logic behind this formula is that when P(A) and P(B) are added, the occasions on which A and B both occur are counted twice. To adjust for this, P(AB) is subtracted. If events A and B are mutually exclusive, the joint probability of A and B is 0. Consequently, the probability that either A or B occurs is simply the sum of the unconditional probabilities of A and B: P (A or B) = P(A) + P(B). What is the probability t

Flashcard 1645902433548

Tags

#reading-9-probability-concepts

Question

Two events, A and B, are independent if and only if [...]

Answer

P(A|B) = P(A),

or equivalently, P(B|A) = P(B).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Multiplication Rule for Independent Events
Two events, A and B, are independent if and only if P(A|B) = P(A), or equivalently, P(B|A) = P(B). That is, the occurrence of one event has no influence on the probability of the occurrence of the other event. In more detail, whether or not B occurs will have no effect on

Flashcard 1645915016460

Tags

#reading-9-probability-concepts

Question

multiplication rule for independent events.

Answer

P(A and B) = P(A) x P(B)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Multiplication Rule for Independent Events
nd B both occur is: P(A and B) = P(A) x P(B) In other words, the probability of A and B both occurring is the product of the probability of A and the probability of B. This relationship is known as the multiplication rule for independent events. What is the probability that a fair coin will come up with heads twice in a row? Two events must occur: heads on the first toss and heads on the second toss. Since the prob

Flashcard 1645917375756

Tags

#reading-9-probability-concepts

Question

For any number of independent events E₁, E₂.....E_n, the probability that all of them occur is:

P(E₁ and E₂..... and E_n) = [...]

Answer

P(E₁) x P(E₂) x ..... x P(E_n)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 4. Multiplication Rule for Independent Events
in the deck, the probability of the first event is 1/52. Since 13/52 = 1/4 of the deck is composed of clubs, the probability of the second event is 1/4. Therefore, the probability of both events is: 1/52 x 1/4 = 1/208. Similarly, for any number of independent events E 1 , E 2 .....E n , the probability that all of them occur is: P(E 1 and E 2 ..... and E n ) = P(E 1 ) x P(E 2 ) x ..... x P(E n ) Example In a bullish market, three shares, chosen from different sectors of the market, have probabilities of 0.6, 0.5 and 0.8 that their share prices will ris

Flashcard 1645930220812

Tags

#reading-9-probability-concepts

Question

The [...] explains the unconditional probability of an event in terms of probabilities conditional on the scenarios.

Answer

total probability rule

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 5. The Total Probability Rule
If we have an event or scenario S, the event not-S, called the complement of S, is written S C . Note that P(S) + P(S C ) = 1, as either S or not-S must occur. The total probability rule explains the unconditional probability of an event in terms of probabilities conditional on the scenarios. P(A) = P(A|S)P(S) + P(A|S C )P(S C ) P(A) = P(A|S 1 )P(S 1 ) + P(A|S 2 )P(S 2 ) + ... + P(A|S n )P(S n ) The first equation is just a special case of the secon

Flashcard 1646448479500

Tags

#reading-9-probability-concepts

Question

Given 3 probabilities to weight an expected value, which one of the outcomes wil happen?

Answer

none of the outcomes actually produces the amount expected

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 6. Expected Value, Variance, and Standard Deviation of a Random Variable
40,000 + 24,000 + 0 = $64,000 Thus, the organizers can expect to take in $64,000. Since it costs $50,000 to stage the event, this translates to a profit of $14,000, so they should certainly go ahead with the venture. It's important to realize that none of the outcomes actually produces an amount of $64,000. This is simply the weighted average of all possible outcomes. Although there is a 50% chance of a loss the big profit that will be made the remaining 50% of the time more than offsets t

Flashcard 1646652427532

Tags

#reading-9-probability-concepts

Question

P (A or B) means the probability of [...] or [...]

Answer

either one event can occur

both events can occur.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 7. Covariance and Correlation
two random variables, R i and R j , is defined as: Alternative notations are corr(R i , R j ) and ρ ij . Properties of correlation: Correlation is a number between -1 and +1. A correlation of 0 indicates an absence of any linear (straight-line) relationship between the variables. Increasingly positive correlation indicates an increasingly strong positive linear relationship (up to 1, which indicates a perfect linear relationship). Increasingly negative correlati

Flashcard 1646910115084

Tags

#reading-9-probability-concepts

Question

Increasingly positive correlation indicates an [...]

Answer

increasingly strong positive linear relationship

(up to 1, which indicates a perfect linear relationship)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 7. Covariance and Correlation
otations are corr(R i , R j ) and ρ ij . Properties of correlation: Correlation is a number between -1 and +1. A correlation of 0 indicates an absence of any linear (straight-line) relationship between the variables. Increasingly positive correlation indicates an increasingly strong positive linear relationship (up to 1, which indicates a perfect linear relationship). Increasingly negative correlation indicates an increasingly strong negative linear relationship (down to -1, which indicates a perfect inverse linear relationship). The correlati

Flashcard 1646945766668

Tags

#reading-9-probability-concepts

Question

If A and B are mutually exclusive P(A or B) = [...]

Answer

P(A) + P(B).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647708343564

Tags

#reading-9-probability-concepts

Question

A rule explaining the unconditional probability of an event in terms of probabilities of the event conditional on mutually exclusive and exhaustive scenarios.

Answer

Total probability rule

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647713848588

Tags

#reading-9-probability-concepts

Question

P(A) = P(AS)+P(AS^C) = P(A|S)P(S) + P(A|S^C)P(S^C)

Answer

Total probability rule

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647723810060

Tags

#reading-9-probability-concepts

Question

The scenarios for the total probability rule must be [...]

Answer

mutually exclusive and exhaustive

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647743470860

Tags

#reading-9-probability-concepts

Question

The probability-weighted average of the possible outcomes of a random variable.

Answer

Expected value

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647772044556

Tags

#reading-9-probability-concepts

Question

The two notations for variance are [...]

Answer

σ²(X) and Var(X).

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647782792460

Tags

#reading-9-probability-concepts

Question

The order of calculation is always [...] , then [...] , then standard deviation.

Answer

expected value

variance

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647821851916

Tags

#reading-9-probability-concepts

Question

Total probability rule for expected value:

E(X)= [...]

Answer

E(X)=E(X|S)P(S)+E(X|S^C)P(S^C)

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647829191948

Tags

#reading-9-probability-concepts

Question

so small or unimportant as to be not worth considering; insignificant.

Answer

Negligible

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1647852522764

Tags

#reading-9-probability-concepts

Question

A diagram with branches emanating from nodes representing either mutually exclusive chance events or mutually exclusive decisions.

Answer

Tree diagram

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1648670936332

Tags

#reading-9-probability-concepts

Question

Covariances are often presented in a square format called a [...]

Answer

covariance matrix.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1648900574476

Tags

#reading-9-probability-concepts

Question

Probabilities reflecting beliefs prior to the arrival of new information.

Answer

Prior probabilities

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1648906341644

Tags

#reading-9-probability-concepts

Question

The probability of an observation, given a particular set of conditions.

Answer

Likelihood

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1648995994892

Tags

#reading-9-probability-concepts

Question

[...] =n(n−1)(n−2)(n−3)…1

Answer

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Flashcard 1652129402124

Tags

#reading-9-probability-concepts

Question

A listing in which the order DOES matter is known as a [...]

Answer

permutation

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Subject 10. Principles of Counting
(The combination formula, or the binomial formula): For example, if you select two of the ten stocks you are analyzing, how many ways can you select the stocks? 10! / [(10 - 2)! x 2!] = 45. An ordered listing is known as a permutation, and the formula that counts the number of permutations is known as the permutation formula. The number of ways that we can choose r objects from a total of n objects, where the order i

Flashcard 1652316048652

Tags

#reading-9-probability-concepts

Question

Regarding counting, there can never be more [...] than [...] for the same problem.

Answer

combinations

permutations

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Parent (intermediate) annotation

combination formula or binominal formula

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

Multinominal formula
A mutual fund guide ranked 18 bond mutual funds by total returns for the year 2014. The guide also assigned each fund one of five risk labels: high risk (four funds), above-average risk (four funds), average risk (t

Flashcard 3663972142348

Question

[default - edit me]

Answer

When you connect two or more computers in a network, each computer becomes more useful. There’s a rule that describes this, called Metcalfe’s Law. Robert Metcalfe was the original designer of the Ethernet structure used in most modern computer networks; his law states that the value (or power) of a network increases in proportion to the square of the number of devices connected to that network. The math is pretty subjective, but Metcalfe’s Law says that two computers connected together are about 4 times as useful as a single computer; if you connect 10 computers, the network is 100 times more powerful, and so forth.

status	not learned	measured difficulty	37% [default]	last interval [days]
repetition number in this series	0	memorised on		scheduled repetition
scheduled repetition interval		last repetition or drill

pdf

cannot see any pdfs

Annotation 3663973715212

Two or more objects, or nodes, that use the network to connect them

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663975288076

A set of communication channels that carry something—speech, TV shows, computer data—between or among nodes

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663976860940

A set of rules that controls network traffic—on a highway, the rules might specify that vehicles drive on the right and pass on the left, and every car and truck must display a license plate to identify it; in a tele- phone network, the rules define the form and use of unique numbers (called “telephone numbers”) to identify each node and establish con- nections between them. To assure that a network operates properly, every node and every channel must follow the rules for that particular network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663978433804

In a data network, the speed of a network is usually shown in millions of bits (or megabits) per second (Mbps)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663980006668

Never underestimate the bandwidth of a station wagon full of floppy disks.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663981579532

Depending on the data transfer speed and the network’s specific requirements, the computer might use a parallel port, a serial port, an Ethernet port, a USB or FireWire port, or a Wi-Fi antenna.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663983152396

Because these connectors and antennas move data in both directions, they are input/output ports or I/O ports, but that term is more often used to describe the computer’s serial and parallel data connectors

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663984725260

A well-designed file-sharing system allows each user to set every file or folder as either “public” or “private.”

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663986298124

your Internet service terminates in just one place, most often in a piece of electronic equipment called a modem (that’s geek-speak for modulator/demodulator, a device that converts between computer data and some other type of communications signal)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663987870988

When you spend that extra money for a DSL or cable Internet link (or fiber optic link), you want easy access to the Internet from every computer in the house. When you connect your network to the modem through a gateway router (shown in Figure 1-2), you can reach the Internet through any computer on that network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663989443852

Within a home or small office network, you can use instant messaging, with or without sound and pictures, to communicate from one room to another. It might be a simple message, such as “Dinner’s ready,” or a more complicated request for information from someone else in the building. And of course, if there are young people in the house, the instant message program will quickly become a channel for gossip and idle conversation.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663991016716

A network printer can either connect directly to the network as a separate node (a printer server) or through one of the network’s computers.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663992589580

A stand-alone video camera (often with a built-in microphone) connected to your home network can have several uses. You can place a camera at the front door to identify visitors, or use one in a nursery or playroom to keep an eye on your children from computers in other parts of the house. Other devices can use special sensors to detect smoke and fires, unlocked or open doors and windows, broken glass, or flooding and other problems and send alerts to the homeowner on a local computer or to a home protection service through the Internet. Combined with a wireless network link, the same kind of security moni- toring can extend to a detached garage, shed, or other separate buildings, even if the house’s wired network does not reach those locations. Chapter 15 explains how to connect and use cameras and other security devices to your network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663994162444

Home automation systems usually use separate wiring from a household data network, but sometimes they’re closely integrated. Home automation can be as simple as turning on outside lights after the sun goes down, or as com- plex as opening and closing drapes, monitoring and adjusting heating and air conditioning, operating a lawn sprinkler, or filling the dog’s water dish. You can also expect the next generation of “smart” kitchen and laundry appliances to include network connections that will allow them to let you know when the roast is cooked or the clothes dryer has completed its fluff cycle.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663995735308

Individual bits only offer two options, so they’re not particularly useful, but when you string eight of them together (into a byte), you can have 256 different combinations (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2). That’s enough to assign a different sequence to every letter of the alphabet (both upper- and lowercase), the ten digits from 0 to 9, spaces between words, and other symbols such as punctuation marks and many letters used in foreign alphabets

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663997308172

The most widely used coding system for converting bytes to characters is called ASCII (American Standard Code for Information Interchange).

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3663998881036

For example, it can divide every second of sound from a microphone or an analog recording into thousands of very short segments and use 16 or 24 bits to specify the content of each segment, or divide a picture into millions of individual points (called pixels, short for picture elements) and use a series of bits to specify the color of each bit

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664000453900

And when you’re using existing circuits such as telephone lines, you don’t have any choice; you must find a way to send one bit at a time, with some additional bits and pauses that identify the beginning of each new byte. This is a serial data communications channel, because you’re sending the bits one after another.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664002026764

you must have a way to convert the text or other output of the computer to the signals used by the transmission medium, and to convert the same signals back again at the other end

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664003599628

Communication over a direct physical connection (such as a wire) between a single origin and destination doesn’t need any kind of address or routing information to tell a message where to go.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664005172492

This kind of connection is great for voice and for simple data links, but it’s not particularly efficient for digital data on a complex net- work that serves many origins and destinations, because a single connection ties up the circuit all the time, even when no data is moving through the channel. The alternative is to send your message to a switching center that will hold it until a link to the destination becomes available. This is known as a store and forward system.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664006745356

To make the network even more efficient, you can divide messages that are longer than some arbitrary limit into separate pieces, called packets or frames. Packets from more than one message can alternate with packets containing other messages as they travel between switching centers, and reassemble themselves into the original messages at the destination.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664008318220

The packets from a single message might alternate with packets from one or more other messages as they move through parts of the network. For example, if you send a message to a recip- ient in another city, the packets usually move through an inter-city channel along with many other messages.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664009891084

Each data packet must also contain yet another set of information: the address of the packet’s destination, the sequence order of this packet relative to other packets in the original transmission, and so forth.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664011463948

The headers (at the beginning of a packet) and trailers (at the end of a packet) attached to each packet include the address of the packet’s desti- nation, information that allows the recipient to confirm that the packet’s content is accurate, and information that the recipient uses to reassemble the packets in the original order. Between the origin and the destination, network routing equipment sometimes adds more headers or trailers that contain routing instructions and other administrative information

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664013036812

network adds and removes headers and trailers at different stages of a communication session.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664014609676

Each layer may attach additional information to the original message and strip off that information after it has done whatever the added information instructed it to do

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664016182540

contain the content of the message, followed by an error-checking sequence, is called a frame.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664017755404

Both wired and wireless networks divide the data stream into frames that contain various forms of handshaking information along with the original data.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664019328268

The network deals with packets and frames at different places during the process of transmitting data. Fortunately, this all happens automatically, so you (as a network user) don’t have to worry about adding or removing them by hand.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664024046860

Therefore, your data stream must include a process called error checking. Error checking is accomplished by adding some kind of standard information to each byte. In a simple computer data network, the handshaking informa- tion is called the parity bit, which tells the device receiving each byte whether the sum of the ones and zeroes inside the byte is odd or even. This value is called a checksum. If the receiving device discovers that the parity bit is not correct, it instructs the transmitter to send the same byte again.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664025619724

More complex networks, including wireless systems, include additional error-checking hand- shaking data with each string of data.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664027192588

First it has to warn the device at the other end that it is ready to send and make sure the intended recipient is ready to accept data. To accomplish this, a series of “handshaking” requests and answers must surround the actual data.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664028765452

it’s important to understand that not every bit that moves through a computer data network is part of the original block of information that arrived at the input computer. In a complex net- work such as a wireless data channel, as much as 40 percent or more of the transmitted data is handshaking and other overhead. It’s all essential, but every one of those bits increases the amount of time that the message needs to move through the network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664030338316

Ethernet was introduced in the 1970s as a method for connecting multiple computers and related equipment in the same building. Ethernet offers several advantages: It’s fast, it’s extremely flexible, it’s relatively easy to install and use, and it’s inexpensive. It has become an industry standard supported by dozens of manufacturers, so you can use different brands of equipment in the same network. Today, more than 85 percent of all local area networks (LANs), including just about every modern home and office network, use some form of Ethernet to provide the physical connection between computers through twisted-pair cables, coaxial cables, or fiber optic cables

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664031911180

One of Ethernet’s most important features is the method it uses to prevent conflicts among nodes, called Carrier Sense Multiple Access with Collision Detection (CSMA/CD). Every time a network node is ready to transmit a frame, it checks if another frame is already using the network; if the network is clear, the node sends the frame. But if the node detects that another frame is using the net- work (a condition called a collision), it waits a random period of time before it tries again. CSMA/CD is important because it allows a relatively large number of computers and other devices to operate through the same network without interference.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664033484044

There are many Ethernet specifications that cover different data transfer speeds and different kinds of cables and connectors. The ones you’re most likely to see in a small LAN include the following: 10Base-T: 10 Mbps through twisted-pair cables 100Base-T or Fast Ethernet: 100 Mbps through twisted-pair cables 1000Base-T or Gigabit Ethernet: 1000 Mbps through twisted-pair or fiber optic cables Wireless or Wi-Fi: any of several systems that use radio signals instead of wires—the latest 802.11n Wi-Fi networks can operate at speeds up to 70 Mbps

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664035056908

A 10Base-T network is adequate for a small home network. It’s faster than most broadband Internet services, so it’s sufficient for handling the inbound and outbound data (including audio and video) that you exchange with the Internet. However, most new network ports, hubs, and switches can handle both 10Base-T and 100Base-T, so there’s very little point to limiting the network to the slower speed. 100Base-T will also allow you to move pictures, music, and videos and play multiplayer games within your own network much faster than a 10Base-T network, and it will not limit the speed of an 802.11n link. Considering the insignificant difference in cost, today’s 100Base-T networks are always a better choice than the older 10Base-T versions.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664036629772

If a 100Base-T network can’t handle 100 Mbps because of interference or some other problem, it will automatically drop down to 10Base-T.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664038202636

A 10Base-T device can work on a 100Base-T network, but it will force the whole network to drop down to 10 Mbps.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664039775500

You might also see the word Ethernet used to identify the connector on a computer, printer, or other network device that mates with an Ethernet cable to connect the device to a network. The instruction manual or the label on every piece of Ethernet-compatible equipment should tell you which type of connection it uses.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664041348364

Twisted-pair cables are bundles of wires in which each pair of wires is twisted together, as shown in Figure 2-3. Because data normally moves in only one direction through each pair of wires, a 10Base-T or 100Base-T network connection uses two pairs—one for each direction. The most common Ethernet cables include a total of eight wires in four color-coded wire pairs, so you can use the remaining wires as spares.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664042921228

Another name for Wi-Fi is wireless Ethernet, because Wi-Fi uses many of the same data-handling rules and specifications as a wired Ethernet network. However, every Wi-Fi packet must include additional handshaking data, so the overall data transfer speed is often slower than a conventional Ethernet link.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664044494092

In a powerline network, computer data moves through a building’s existing electric wiring. Each computer connects through a parallel port, a USB port, or an Ethernet port to a data adapter that plugs directly into an AC wall outlet. The same power transformer that feeds your house wiring also isolates your data network from your neighbors

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664046066956

The most widely used standard for powerline networks is called HomePlug. The greatest advantage of HomePlug and other powerline networks is that the wires are already in place. Every AC wall socket in the house can double as a network connection point. It’s also more secure than Wi-Fi, and it can reach greater distances than a Wi-Fi network with just one base station. Wi-Fi signals are often blocked by thick walls and other obstacles that make no difference to a powerline system.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664047639820

You must plug all your powerline adapters directly into wall outlets. Surge protectors and powerline conditioners often absorb powerline network data, because they see the data as “noise” on the AC power voltage. Conversely, if you’re using a powerline net- work, you will want to connect your stereo or home theater system to power conditioners to filter out the noise produced by the network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664049212684

Two more home networking methods are possible, but they’re almost always provided as supplements to other services. These systems use the internal telephone wiring that connects extension telephones in several rooms or the coaxial cable (coax) that provides cable TV signals.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664050785548

There’s one more concept that every network planner should understand: the difference between data terminal equipment (DTE) and data communications equipment or data circuit-terminating equipment (DCE)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664052358412

Data can move through a wire in only one direction. When a data link sends and receives signals at the same time, it must use separate wires to send data from the DTE to the DCE, and from the DCE to the DTE. Therefore, a network device uses separate inputs and outputs on the same multipin connector. The specific pin assignment is different in different connection types, but the inputs and outputs are always different pins or sockets.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664053931276

Therefore, when you connect two pieces of equipment, the outputs at each end must go to inputs at the other end. If Pin 2 on one device is an output, Pin 2 on the other device must be an input. Most standard data cables connect each connector pin to the same numbered pin at the other end, so connecting two devices through a cable is exactly the same as plugging one device directly into another.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664055504140

When you connect a terminal to a control device, the output pins on the DTE device connect to the input pins on the DCE device.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664057077004

Direct computer-to-computer communication requires a special cable because you can’t connect a DTE device directly to another DTE device. When you connect two DTE devices with serial data ports, you connect the output on one computer to the output on the other computer, and the input to the input, so neither computer will actually receive any data. Therefore, you must flip the connections, so each output connects to an input. A cable or adapter that connects output pins to input pins is called a null modem.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664058649868

Most of the time, we think of a computer network as a structure that can link one computer to any other computer connected to the same network. But sometimes all you need is a direct connection between two computers. This kind of connection is called a point-to-point network.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664060222732

For example, if you’re in a meeting where some- body asks for a copy of a report or drawing, you could use the built-in infrared network tools built into many laptop computers to shoot the file across the table from your computer to your colleague’s. Or if you want to copy a file from a friend’s computer, you could plug a transfer cable into both machines or set up a point-to-point Wi-Fi link

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664061795596

Most Wi-Fi networks connect wireless nodes to a LAN through a wireless access point, but Wi-Fi network adapters can also support wireless links directly from one computer to another. This kind of connection is called an ad hoc network, because it’s usually set up as a temporary link rather than as part of a permanent network infrastructure (wireless networks with one or more central access points are called infrastructure networks)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664063368460

Infrared connections use invisible flashing light (it’s invisible because it uses frequencies outside the range of human sight) to exchange data between computers, mobile telephones, digital cameras, and other devices. Most of the wireless remote control units that you use with your television, DVD player, and home stereo system also use infrared light signals. Infrared channels are often called IrDA connections, because the Infrared Data Association (IrDA) has set the standards for infrared communication.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664064941324

Many laptop computers have built-in IrDA ports, usually in an incon- spicuous location along the edge of the case. The IrDA port is usually an infrared lens under a transparent plastic cover, like the one shown in Figure 2-8. The camera captured the flashing infrared light, even though it’s not normally visible to the human eye.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664066514188

As you have probably noticed with your TV’s remote control, infrared signals can bounce off walls and other objects, so it’s not absolutely necessary to point a pair of IrDA ports directly at each other, especially when they’re both indoors. When two computers with active IrDA ports are in the same room, they will usually detect each other automatically.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664068087052

The infrared port on a laptop computer can detect an IrDA signal from another computer in the same room and automatically set up a network link between the two devices. It’s best, then, to disable the infrared port anytime you’re not planning to use it. To disable or enable infrared communications in Windows, open the Device Manager (Control Panel System Hardware Device Manager), expand the list of infrared devices, right-click the name of the infrared port, and choose Disable or Enable from the pop-up menu

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664069922060

This has several didactic advantages worth mentioning: both posets and monoids are themselves special kinds of categories, which in a certain sense represent the two “dimen- sions” (objects and arrows) that a general category has.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664071494924

Many phenomena occurring in categories can best be understood as generalizations from posets or monoids. On the other hand, the categories of posets (and monotone maps) and monoids (and homomorphisms) provide two further, quite diﬀerent examp- les of categories in which to consider various concepts. The notion of a limit, for instance, can be considered both in a given poset and in the category of posets.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664073067788

The selection of material was easy. There is a standard core that must be included: categories, functors, natural transformations, equi- valence, limits and colimits, functor categories, representables, Yoneda’s lemma, adjoints, and monads. That nearly ﬁlls a course. The only “optional” topic inclu- ded here is cartesian closed categories and the λ-calculus, which is a must for computer scientists, logicians, and linguists. Several other obvious further topics were purposely not included: 2-categories, topoi (in any depth), and monoidal categories. These topics are treated in Mac Lane, which the student should be able to read after having completed the course.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664074640652

What is category theory? As a ﬁrst approximation, one could say that category theory is the mathematical study of (abstract) algebras of functions.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664076213516

group theory is the abstraction of the idea of a system of permutations of a set or symmetries of a geometric object

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664077786380

category theory arises from the idea of a system of functions among some objects

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664079359244

We think of the composition g ◦ f as a sort of “product” of the functions f and g, and consider abstract “algebras” of the sort arising from collections of functions. A category is just such an “algebra,” consisting of objects A,B,C,... and arrows f : A → B, g : B → C, ..., that are closed under composition and satisfy certain conditions typical of the composition of functions.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664080932108

category theory was invented in the tradition of Felix Klein’s Erlanger Programm, as a way of studying and characterizing diﬀerent kinds of mathematical structures in terms of their “admissible trans- formations.” The general notion of a category provides a characterization of the notion of a “structure-preserving transformation,” and thereby of a species of structures admitting such transformations

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664082504972

1945 Eilenberg and Mac Lane’s “General theory of natural equivalences” was the original paper, in which the theory was ﬁrst formulated.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664084077836

Late 1940s The main applications were originally in the ﬁelds of algebraic topology, particularly homology theory, and abstract algebra

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664085650700

1950s A. Grothendieck et al. began using category theory with great success in algebraic geometry.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664087223564

1960s F.W. Lawvere and others began applying categories to logic, revealing some deep and surprising connections.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664088796428

1970s Applications were already appearing in computer science, linguistics, cognitive science, philosophy, and many other areas.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664090369292

For example, the important notion of an adjoint functor occurs in logic as the existential quantiﬁer and in topology as the image operation along a continuous function. From a categorical point of view, these turn out to be essentially the same operation.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664091942156

The concept of adjoint functor is in fact one of the main things that the reader should take away from the study of this book. It is a strictly category-theoretical notion that has turned out to be a conceptual tool of the ﬁrst magnitude—on par with the idea of a continuous function.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664093515020

In fact, just as the idea of a topological space arose in connection with con- tinuous functions

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664095087884

the notion of a category arose in order to deﬁne that of a functor, at least according to one of the inventors. The notion of a functor arose—so the story goes on—in order to deﬁne natural transformati- ons.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664096660748

everywhere that functions are, there are categories. Indeed, the subject might better have been called abstract function theory,

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664098233612

Let f be a function from a set A to another set B, we write f : A → B. To be explicit, this means that f is deﬁned on all of A and all the values of f are in B. In set theoretic terms, range(f) ⊆ B.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664101641484

Now suppose we also have a function g : B → C, then there is a composite function g ◦ f : A → C, given by (g ◦ f)(a)=g(f(a)) a ∈ A.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664104000780

Now this operation “◦” of composition of functions is associative, as follows. If we have a further function h : C → D and form h ◦ g and g ◦ f, then we can compare (h ◦ g) ◦ f and h ◦ (g ◦ f) as indicated in the diagram given above. It turns out that these two functions are always identical, (h ◦ g) ◦ f = h ◦ (g ◦ f ) since for any a ∈ A,wehave ((h ◦ g) ◦ f)(a)=h(g(f(a))) = (h ◦ (g ◦ f))(a)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664106360076

By the way, this is, of course, what it means for two functions to be equal: for every argument, they have the same value.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664107932940

Finally, note that every set A has an identity function 1 A : A → A given by 1 A (a)=a. These identity functions act as “units” for the operation ◦ of composition, in the sense of abstract algebra. That is to say, f ◦ 1 A = f =1 B ◦ f for any f : A → B.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664109505804

Deﬁnition 1.1. A category consists of the following data:
• Objects: A,B,C,...
• Arrows : f,g,h,...
• For each arrow f, there are given objects dom(f), cod(f) called the domain and codomain of f. We write f : A → B to indicate that A =dom(f)andB =cod(f).
• Given arrows f : A → B and g : B → C, that is, with cod(f)=dom(g)

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664111865100

there is given an arrow g ◦ f : A → C called the composite of f and g.
• For each object A, there is given an arrow 1 A : A → A called the identity arrow of A.
These data are required to satisfy the following laws:
• Associativity: h ◦ (g ◦ f)=(h ◦ g) ◦ f for all f : A → B, g : B → C, h : C → D.
• Unit: f ◦ 1 A = f =1 B ◦ f for all f : A → B

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664114224396

A category is anything that satisﬁes this deﬁnition—and we will have plenty of examples very soon. For now I want to emphasize that, unlike in Section 1.2, the objects do not have to be sets and the arrows need not be functions. In this sense, a category is an abstract algebra of functions, or “arrows” (sometimes also called “morphisms”), with the composition operation “◦” as primitive. If you are familiar with groups, you may think of a category as a sort of generalized group.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Annotation 3664115797260

A “homomorphism of categories” is called a functor.

status	not read	reprioritisations
last reprioritisation on		suggested re-reading day
started reading on		finished reading on

pdf

cannot see any pdfs

Edited, memorised or added to reading queue

on 18-Dec-2018 (Tue)

Parent (intermediate) annotation

Original toplevel document (pdf)

Parent (intermediate) annotation

Original toplevel document

Parent (intermediate) annotation

Original toplevel document